Giải:

a; Thời gian người đó lên dốc là: 120 : 4 = 30 (s)

   Thời gian người đó đi thêm 60 m là: 60 : 5 = 12 (s)

b; Áp dụng công thức: v_tb = \(\dfrac{S_1+S_2}{t_1+t_2}\) 

Vận tốc trung bình của người đó trên cả quãng đường là:

          \(\dfrac{120+60}{30+12}\) = \(\dfrac{30}{7}\) (m/s)

Kết luận: a; Thời gian người đó lên dốc là: 30 giây

                   Thời gian người đó đi nốt quãng đường 60m là 12 giây

               b; Vận tốc trung bình trên của người đó là: \(\dfrac{30}{7}\)m/s

đổi 24\(\dfrac{3}{5}\)m=14,4m; 18\(\dfrac{9}{20}\)phút=8,1phút

Thời gian Nhung đi từ A đến B là

14,4 chia 8,2 ≈ 1,8 phút

Thời gian Nhung đi từ B đến C là

8,1-1,8=6,3 phút

Quãng đường từ C đến B là

14,4-8,6=5,8m

Vận tốc của Nhung khi di chuyển từ B đến C là

5,8 chia 6,3 ≈ 0,92 m/phút

Thời gian đi được nửa quãng đường đầu :

\(t_1=\dfrac{s_1}{v_1}=\dfrac{2}{20}=0,1\left(h\right)\)

Thời gian đi được nửa quãng đường sau :

\(t_2=\dfrac{s_2}{v_2}=\dfrac{2}{10}=0,2\left(h\right)\)

Tốc độ trung bình cả quãng đường từ nhà đến trường :

\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{2+2}{0,1+0,2}=13,33\left(km/h\right)\)

                        Giải:

  a; 60m = 0,06 km; 10s = \(\dfrac{1}{360}\) giờ; 20m = 0,02 km

Vận tốc của người đó đi trên quãng đường đầu là:

           0,06 : \(\dfrac{1}{360}\) = 21,6 (km/h)

b;  Thời gian người đó đi hết quãng đường sau là:

            0,02 : 3,6 = \(\dfrac{1}{180}\) (giờ)

         Áp dụng công thức V_tb = \(\dfrac{S_1+S_2}{t_1+t_2}\) ta có: 

     Tốc độ của xe đó trên cả 2 quãng đường là:

          \(\dfrac{0,06+0,02}{\dfrac{1}{360}+\dfrac{1}{180}}\)  = 9,6 (km/h)

Kết luận: a; Vận tốc của người đó trên quãng đường đầu là 21,6 km

               b; Vận tốc của người đó trên cả quãng đường là 9,6 km

Vận tốc của người đó trên cả quãng đường là:

\(t_1=\dfrac{s_1}{v_1}=\dfrac{15}{30}=0,5\left(h\right)\)

\(t_2=30\left(phút\right)=0,5\left(h\right)\)

\(t_3=10\left(phút\right)=\dfrac{1}{6}\left(h\right)\)

Tốc độ trung bình của xe máy trên cả đoạn đường :

\(v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2+t_3}=\dfrac{15+45.0,5+6}{\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{6}}=\dfrac{43,5}{\dfrac{7}{6}}\sim37,3\left(km/h\right)\)

                             Giải:

Thời gian ô tô xuất phát trước xe khách là: 10 giờ - 7 giờ = 3 giờ

Khi xe khách xuất phát ô tô cách xe khách là: 30 x 3 = 90 (km/h)

Hai xe gặp nhau sau: 90 : (60 - 30) = 3 (giờ)

Lúc gặp nhau cách A là: 60 x 3 = 180 (km)

Lúc gặp nhau cách B là:  230 - 180 = 50 (km)

Kết luận: Hai xe gặp nhau sau 3 giờ 

              Vị trí gặp nhau cách A là 180 km, cách B là 50 km

                 Giải:

Thời gian người đó đi quãng đường đầu là: t₁ =  8 : 12 = \(\dfrac{2}{3}\)(giờ)

Thời gian người đó nghỉ sửa xe là: t₂ = 40 phút = \(\dfrac{2}{3}\) giờ

Thời gian người đó đi hết quãng đường sau là: t₃ = 12 : 9 = \(\dfrac{4}{3}\) (giờ)

Ta có đồ thị quãng đường thời gian là:

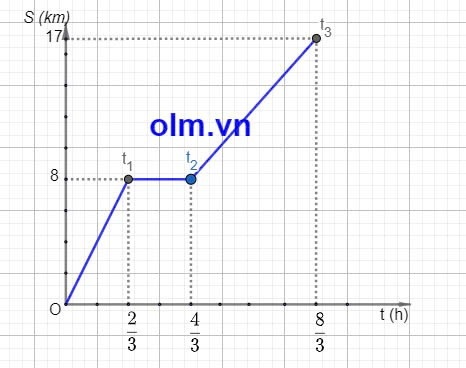
Tốc độ của vận động viên là:

`v = S : t = 100 : 10,5  \approx 9,52 (m`/`s`)`

Vậy: Tốc độ của vận động viên khoảng: `9,52 m`/`s`

Số p của mỗi nguyên tử của nguyên tố X = số e. Vậy số p là:

12 : 2 = 6 (p)

⇒ Điện tích hạt nhân là: +6

Số n của mỗi nguyên tử của nguyên tố X là:

12 : 2 = 6 (n)

Khối lượng mỗi nguyên tử của nguyên tố X là:

6 + 6 = 12 (amu)