\(\left\{{}\begin{matrix}\dfrac{3x}{4}+\dfrac{7y}{3}=41\\\dfrac{5x}{2}-\dfrac{3y}{5}=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+28y=492\\25x-6y=110\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}225x+700y=12300\\225x-54y=990\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}700y+54y=12300-990\\9x+28y=492\end{matrix}\right.\)

\(\)\(\Leftrightarrow\left\{{}\begin{matrix}y=15\\x=8\end{matrix}\right.\)

Vậy (x;y) = (8;15) 

Em đăng đúng môn nhé.

Ta chứng minh \(\left(n,n+1\right)=1\) với mọi số tự nhiên n. Thật vậy, đặt \(\left(n,n+1\right)=d\left(d\inℕ^∗\right)\), khi đó \(\left\{{}\begin{matrix}n⋮d\\n+1⋮d\end{matrix}\right.\) \(\Rightarrow\left(n+1\right)-n⋮d\) \(\Rightarrow1⋮d\Rightarrow d=1\). Vậy \(\left(n,n+1\right)=1\). 

Xét số tự nhiên \(k\) bất kì sao cho \(1\le k\le35\). Theo đề bài kết hợp với \(\left(n,n+1\right)=1\), dễ thấy \(\left(n,n+k\right)\ge k\). Đặt \(\left(n,n+k\right)=d'\left(d'\ge k\right)\), khi đó \(\left\{{}\begin{matrix}n⋮d'\\n+k⋮d'\end{matrix}\right.\Rightarrow\left(n+k\right)-n⋮d'\) \(\Rightarrow k⋮d'\). Nhưng do \(d'\ge k\) nên \(d'=k\). Vì \(n⋮d'\) ,suy ra \(n⋮k\) (đpcm)

n_CO2=0,1(mol)            n_H2O=0,1(mol)

m_{O(trong A)}=2,2 - m_C - m_H=2,2-0,1.12-0,1.2=0,8 (g)

n_{O(trong A)}=\(\dfrac{0,8}{16}=0,05\left(mol\right)\)

Gọi CTĐGN của hợp chất A là C_xH_yO_z

Ta có x:y:z=n_C:n_H:n_O=0,1:0,1:0,05=2:2:1

Vậy CTĐGN của hợp chất A là C₂H₂O

a)

Trích mẫu thử

Cho mẫu thử vào nước

- mẫu thử nào không tan là $C_6H_6$

Cho giấy quỳ tím vào hai mẫu thử còn lại :

- mẫu thử nào làm quỳ tím hóa đỏ là $CH_3COOH$

- mẫu thử nào không đổi màu quỳ tím là $C_2H_5OH$

b)

Trích mẫu thử

Cho giấy quỳ tím vào các mẫu thử :

- mẫu thử nào làm quỳ tím hóa đỏ là $CH_3COOH$

Cho dung dịch $AgNO_3/NH_3$ vào mẫu thử còn :

- mẫu thử nào tạo kết tủa trắng bạc là Glucozo

$C_6H_{12}O_6 + Ag_2O \xrightarrow{NH_3} 2Ag + C_6H_{12}O_7$

- mẫu thử nào không hiện tượng là saccarozo

c)

Trích mẫu thử

Cho dung dịch $AgNO_3/NH_3$ vào mẫu thử :

- mẫu thử nào tạo kết tủa trắng bạc là Glucozo

$C_6H_{12}O_6 + Ag_2O \xrightarrow{NH_3} 2Ag + C_6H_{12}O_7$

Cho dung dịch Iot vào mẫu thử còn :

- mẫu thử nào xuất hiện màu xanh tím là tinh bột

- mẫu thử không hiện tượng là xenlulozo

b,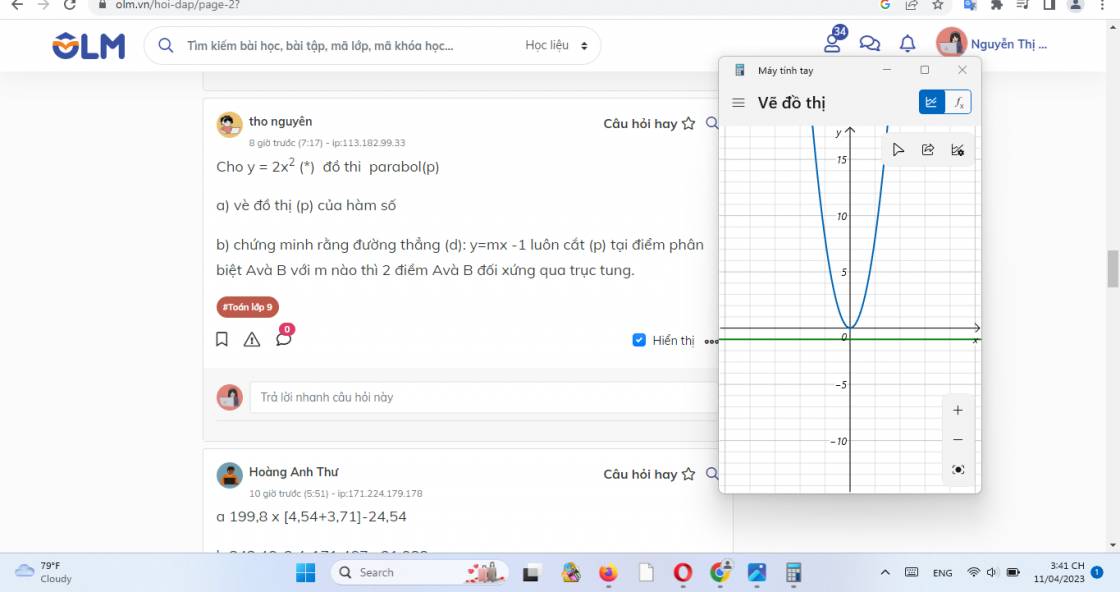 

Giả sử m = 0 thì đt có dạng y = -1

Quan sát hai đồ htij trên hình vẽ em sẽ thấy

parapol (p) và đt d không cắt nhau vậy việc chứng minh (p) và (d) cắt nhau tại hai điểm phân biệt với mọi m là không thể xảy ra 

a, - Dẫn từng khí qua Ca(OH)₂ dư.

+ Có tủa trắng: CO₂

PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)

+ Không hiện tượng: CH₄, C₂H₄, C₂H₂. (1)

- Dẫn khí nhóm (1) qua dd AgNO₃/NH₃.

+ Xuất hiện tủa vàng: C₂H₂.

PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)

+ Không hiện tượng: CH₄, C₂H₄. (2)

- Dẫn khí nhóm (2) qua dd brom dư.

+ Dd nhạt màu dần: C₂H₄.

PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)

+ Không hiện tượng: CH₄. 

b, - Dẫn từng khí qua dd Ca(OH)₂

+ Xuất hiện tủa trắng: CO₂

PT: \(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)

+ Không hiện tượng: CH₄, C₂H₂ và O₂. (1)

- Dẫn khí nhóm (1) qua dd AgNO₃/NH₃.

+ Có tủa vàng: C₂H₂.

PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)

+ Không hiện tượng: CH₄ và O₂. (2)

- Cho tàn đóm đỏ vào 2 khí nhóm (2)

+ Que đóm bùng cháy: O₂.

+ Không hiện tượng: CH₄.

c, - Dẫn từng khí qua dd Ca(OH)₂.

+ Có tủa trắng: SO₂, CO₂ (1)

PT: \(SO_2+Ca\left(OH\right)_2\rightarrow CaSO_3+H_2O\)

\(CO_2+Ca\left(OH\right)_2\rightarrow CaCO_3+H_2O\)

+ Không hiện tượng: C₂H₂, CH₄ và C₂H₄. (2)

- Dẫn khí nhóm (1) qua dd nước brom dư.

+ Dd nhạt màu dần: SO₂

PT: \(SO_2+Br_2+2H_2O\rightarrow2HBr+H_2SO_4\)

+ Không hiện tượng: CO₂.

- Dẫn khí nhóm (2) qua dd AgNO₃/NH₃

+ Có tủa vàng: C₂H₂.

PT: \(C_2H_2+2AgNO_3+2NH_3\rightarrow Ag_2C_2+2NH_4NO_3\)

+ Không hiện tượng: CH₄, C₂H₄ (3)

- Dẫn khí nhóm (3) qua dd brom dư.

+ Dd nhạt màu dần: C₂H₄

PT: \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)

+ Không hiện tượng: CH₄.

A.

a, \(n_{CH_3COOH}=0,2.1=0,2\left(mol\right)\)

PT: \(Mg+2CH_3COOH\rightarrow\left(CH_3COO\right)_2Mg+H_2\)

Theo PT: \(n_{Mg}=n_{H_2}=\dfrac{1}{2}n_{CH_3COOH}=0,1\left(mol\right)\)

\(\Rightarrow m=m_{Mg}=0,1.24=2,4\left(g\right)\)

\(V=V_{H_2}=0,1.22,4=2,24\left(l\right)\)

b, \(C_2H_5OH+O_2\underrightarrow{^{mengiam}}CH_3COOH+H_2O\)

Theo PT: \(n_{C_2H_5OH}=n_{CH_3COOH}=0,2\left(mol\right)\)

\(\Rightarrow m_{C_2H_5OH}=0,2.46=9,2\left(g\right)\)

\(\Rightarrow V_{ddC_2H_5OH}=\dfrac{9,2}{0,8}=11,5\left(ml\right)\)