Sĩ số lớp 6A1 là 48 hsinh , trong đó có 30 hsinh nữ . Tính tỉ số giữa số hsinh nữ và sĩ số cả lớp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1: Diện tích nền nhà là:
\(4,2\cdot20,5=86,1\left(m^2\right)\)

Câu 1:
\(-9\%=-\dfrac{9}{100}=-0,09\)
\(59\%=\dfrac{59}{100}=0,59\)
\(-542\%=-\dfrac{542}{100}=-5,42\)
Câu 10:
\(0,68=\dfrac{68}{100}=68\%\)
\(-0,02=-\dfrac{2}{100}=-2\%\)
\(-2,36=-\dfrac{236}{100}=-236\%\)

a: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\) và \(MA\cdot MB=HM^2\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right);NA\cdot NC=NH^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\left(3\right);AB^2=BH\cdot BC;AC^2=CH\cdot BC\)
Từ (1) và (3) suy ra \(AM\cdot AB=HB\cdot HC\)
b: Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>\(HA^2=HM^2+HN^2\)
=>\(HB\cdot HC=MA\cdot MB+NA\cdot NC\)
d: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)
=>\(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
e: Xét ΔAHB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM=\dfrac{BH^2}{BA}\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(CN\cdot CA=CH^2\)
=>\(CN=\dfrac{CH^2}{CA}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(BC=\dfrac{AB\cdot AC}{AH}\)
\(BM\cdot CN\cdot BC=\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{CA}\cdot\dfrac{AB\cdot AC}{AH}\)
\(=\dfrac{BH^2}{AH}\cdot CH^2=\dfrac{\left(BH\cdot CH\right)^2}{AH}=\dfrac{AH^4}{AH}=AH^3\)
mà AH=MN(AMHN là hình chữ nhật)
nên \(BM\cdot CN\cdot BC=MN^3\)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
b: DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
mà BD cắt AE tại F
nên F là trung điểm của AE
=>CF là đường trung tuyến của ΔAEC

Sửa đề: Chứng minh \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
Bài làm:
\(VT=\left(a+b\right)^3=\left(a+b\right)\left(a+b\right)\left(a+b\right)\\ =\left(a^2+ab+ab+b^2\right)\left(a+b\right)\\ =\left(a^2+2ab+b^2\right)\left(a+b\right)\\ =a^3+2a^2b+ab^2+a^2b+2ab^2+b^3\\ =a^3+3a^2b+3ab^2+b^3=VP\left(DPCM\right)\)

\(\dfrac{24}{21}\cdot\dfrac{9}{8}=\dfrac{8}{7}\cdot\dfrac{9}{8}=\dfrac{9}{7}\)

Hiệu số phần bằng nhau là 4-1=3(phần)
Số bé là 120:3x1=40
Số lớn là 40+120=160

Nếu xóa chữ số 0 ở hàng đơn vị của số thứ nhất thì ta được số thứ hai nên số thứ nhất=10 lần số thứ hai
9 lần số thứ hai là số thứ nhất-số thứ hai=459
=>Số thứ hai là 459:9=51
Số thứ nhất là 51x10=510
Nếu xóa chữ số 0 ở hàng đơn vị của số thứ nhất thì ta được số thứ hai nên số thứ nhất=10 lần số thứ hai
9 lần số thứ hai là số thứ nhất-số thứ hai=459
=>Số thứ hai là 459:9=51
Số thứ nhất là 51x10=510
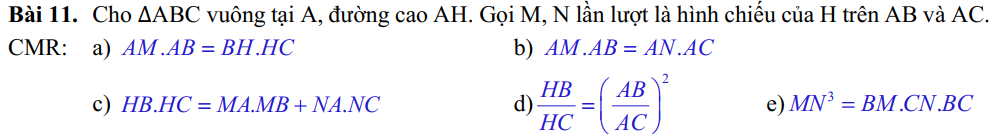
Tỉ số giữa số học sinh nữ với tổng số học sinh là:
\(\dfrac{30}{48}=\dfrac{30:6}{48:6}=\dfrac{5}{8}\)