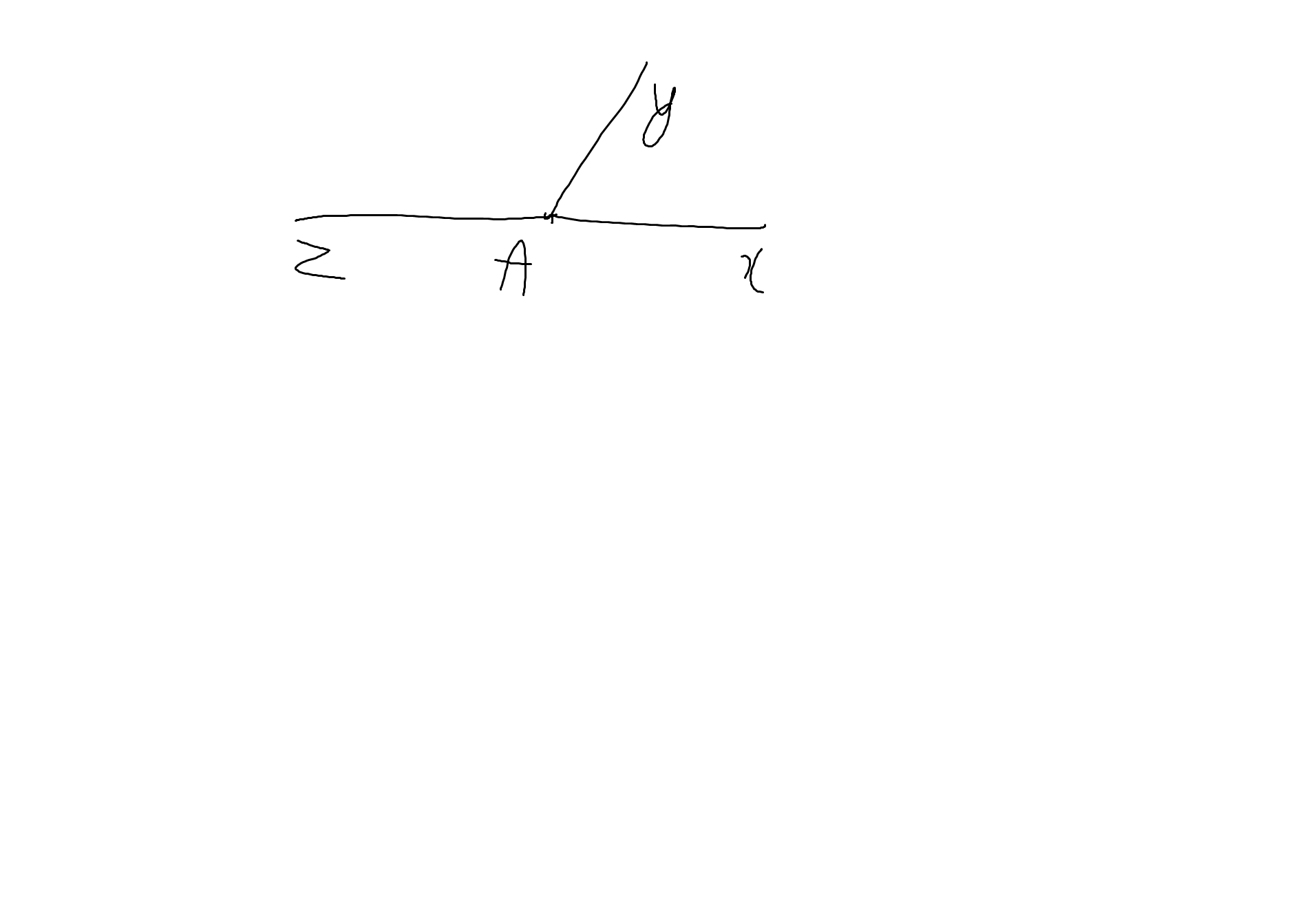vẽ xay = 400 . Vẽ yaz là góc kề bù với góc zay
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\left(x+1\right)=2+4+6+...+2500\)
=>\(x\left(x+1\right)=2\cdot\left(1+2+3+...+1250\right)\)
=>\(x\left(x+1\right)=2\cdot\dfrac{1250\cdot1251}{2}=1250\cdot1251\)
=>x=1250
`x . (x + 1) = 2 + 4 +6 + ...+ 2500`
`=> x . (x + 1) = (2500 + 2) . [(2500 - 2) : 2 + 1] : 2`
`=> x . (x + 1) = 2502 . 1250 : 2`
`=> x . (x + 1) =1251. 1250`
`=> x . (x + 1) = (1250+1). 1250`
Do x là số nhiên, nên `x = 1250.`
Vậy `x = 1250 `
----------------------------
Phân tích thành nhân từ cũng được nhé:
`=> x . (x + 1) =1251. 1250`
`=> x^2 + x - 1251. 1250 = 0`
`=> x^2 + 1251x - 1250x - 1251. 1250 = 0`
`=> (x^2 + 1251x) - (1250x + 1251. 1250) = 0`
`=> x(x + 1251) - 1250 (x + 1251) = 0`
`=> (x-1250)(x+1251) = 0`
`=> x = 1250` hoặc `x = -1251`
Mà `x` là số tự nhiên nên `x = 1250`

Nửa chu vi sân trường là 142:2=71(m)
Chiều dài sân trường là (71+13):2=84:2=42(m)
Chiều rộng sân trường là 42-13=29(m)
Diện tích sân trường là:
42x29=1218(m2)

Tứ giác \(ABCD\) là hình bình hành
=> \(\widehat{ADC}=\widehat{ABC}\)
Lại có: `\(\)BF, DE` lần lượt là phân giác của \(\widehat{ABC}\) và \(\widehat{ADC}\)
=> \(\widehat{ADE}=\widehat{EDC}=\widehat{ABF}=\widehat{FBC}\)
Mà `AB` // `DC =>` \(\widehat{ABF}=\widehat{BFC}\) (2 góc so le trong)
=> \(\widehat{EDC}=\widehat{BFC}\)
Mà 2 góc đó là 2 góc đồng vị
`=> DE` // `BF` (đpcm)

a: Ta có: \(AE=EB=\dfrac{AB}{2}\)
\(CF=FD=\dfrac{CD}{2}\)
mà AB=CD
nên AE=EB=CF=FD
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét tứ giác BFDE có
BE//DF
BE=DF
Do đó: BFDE là hình bình hành
=>BF//DE
=>EM//FN
Ta có AECF là hình bình hành
=>AF//CE
=>MF//EN
Xét tứ giác EMFN có
EM//FN
EN//FM
Do đó: EMFN là hình bình hành
c: Ta có: EMFN là hình bình hành
=>EF cắt MN tại trung điểm của mỗi đường(1)
Ta có: AECF là hình bình ahfnh
=>AC cắt EF tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AC,EF,MN đồng quy