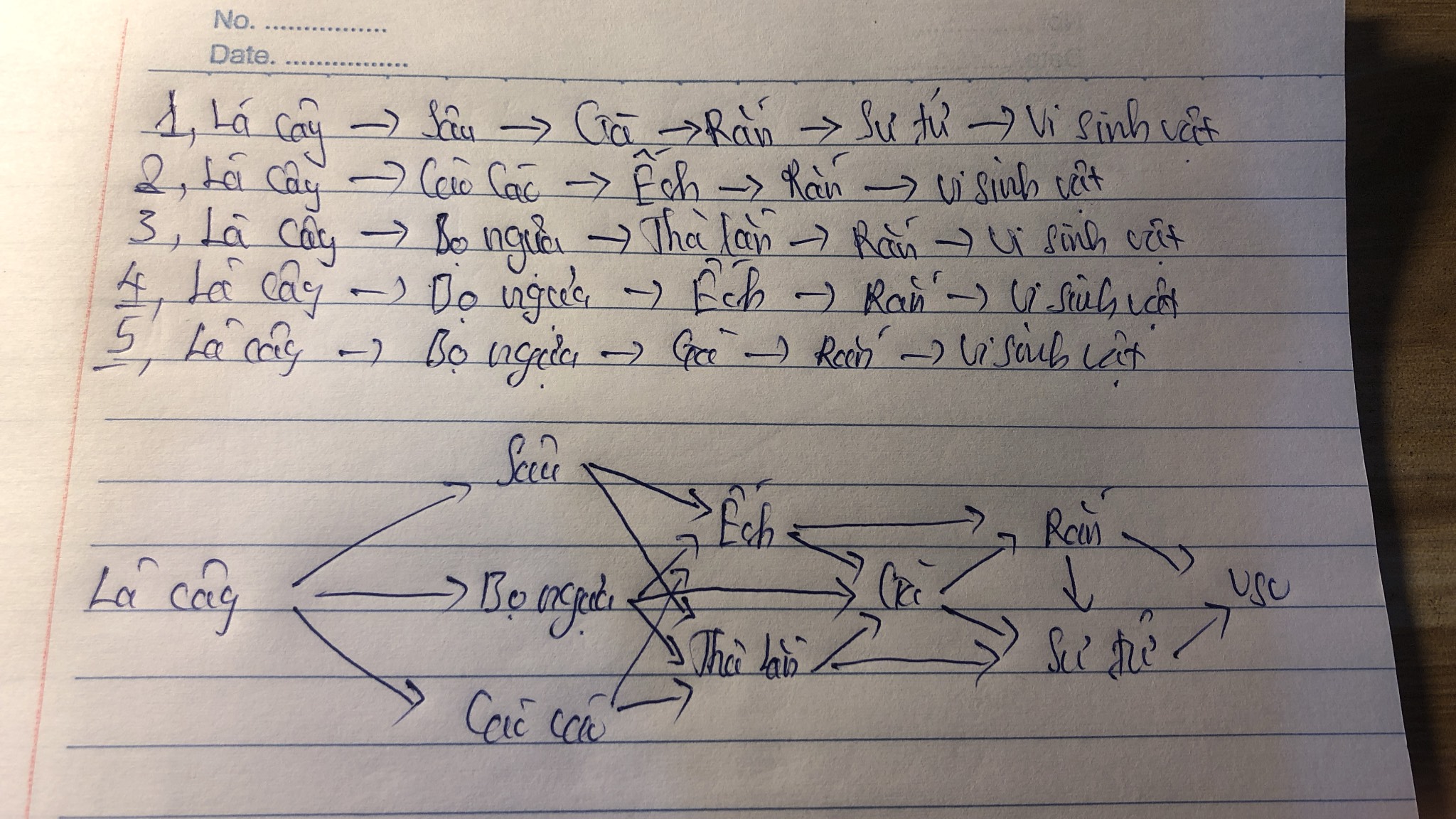
Câu 1 : Cho hàm số y = 1/2x² có đồ thị là parabol và đường thẳng d có phương trình là y = x + m. Tìm m để d cắt parabol tại hai điểm phân biệt A( x1; y1) B(x2 ; y2) và thỏa mãn 1/2y1 + 1/2y2 = 2
Câu 2: cho một tam giác có đường cao với độ dài bằng một nửa độ dài cạnh đáy tương ứng nếu tăng chiều cao thêm 2 m và cạnh tương ứng tăng thêm 6 m thì được một tam giác có diện tích gấp đôi diện tích tam giác ban đầu Tính diện tích của tam giác ban đầu