\(A=\left(1^1+2^2+3^3+...+2022^{2022}\right)^{2023}\cdot\left(8^2-576:3^2\right)^{2024}\)

\(=\left(1^1+2^2+3^3+...+2022^{2022}\right)^{2023}\cdot\left(64-576:9\right)^{2024}\)

\(=\left(1^1+2^2+3^3+...+2022^{2022}\right)^{2023}\cdot\left(64-64\right)^{2024}\)

=0

Đúng 

Bài 2:

a: \(45\%\cdot x-0,385=-1,685\)

=>\(0,45x=-1,685+0,385=-1,3\)

=>\(x=-\dfrac{1.3}{0,45}=-\dfrac{26}{9}\)

b: \(\left(3\dfrac{1}{4}+2x\right)\cdot\dfrac{2}{3}=2\)

=>\(2x+\dfrac{13}{4}=2:\dfrac{2}{3}=3\)

=>\(2x=3-\dfrac{13}{4}=-\dfrac{1}{4}\)

=>\(x=-\dfrac{1}{4}:2=-\dfrac{1}{8}\)

c: \(\dfrac{3}{4}+\dfrac{1}{4}:x=-3\)

=>\(\dfrac{1}{4}:x=-3-\dfrac{3}{4}=-\dfrac{15}{4}\)

=>\(x=\dfrac{1}{4}:\dfrac{-15}{4}=\dfrac{-1}{15}\)

d: \(2x-0,75=-\dfrac{7}{12}\)

=>\(2x=-\dfrac{7}{12}+0,75=\dfrac{2}{12}\)

=>\(x=\dfrac{1}{12}\)

e: \(\dfrac{4}{9}-\dfrac{7}{12}x=\dfrac{1}{3}\)

=>\(\dfrac{7}{12}x=\dfrac{4}{9}-\dfrac{1}{3}=\dfrac{1}{9}\)

=>\(x=\dfrac{1}{9}:\dfrac{7}{12}=\dfrac{1}{9}\cdot\dfrac{12}{7}=\dfrac{4}{21}\)

Bài 1:

a: \(\left(\dfrac{7}{5}+\dfrac{-5}{11}\right)-\left(\dfrac{6}{11}-\dfrac{3}{5}\right)-2023^0\)

\(=\dfrac{7}{5}-\dfrac{5}{11}-\dfrac{6}{11}+\dfrac{3}{5}-1\)

\(=2-1-1=0\)

b: \(\dfrac{2}{-9}\cdot\dfrac{7}{15}+\dfrac{-2}{9}\cdot\dfrac{8}{15}+1\dfrac{2}{3}\)

\(=\dfrac{-2}{9}\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+\dfrac{5}{3}\)

\(=-\dfrac{2}{9}+\dfrac{5}{3}=\dfrac{13}{9}\)

c: \(\dfrac{1}{3}+\dfrac{-7}{12}+\dfrac{2}{3}+\dfrac{-5}{12}\)

\(=\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(-\dfrac{7}{12}-\dfrac{5}{12}\right)\)

=1-1

=0

d: \(\dfrac{3}{7}\cdot\dfrac{-9}{13}+\dfrac{3}{7}\cdot\dfrac{-4}{13}+1\dfrac{3}{7}\)

\(=\dfrac{3}{7}\left(-\dfrac{9}{13}-\dfrac{4}{13}\right)+1+\dfrac{3}{7}\)

\(=-\dfrac{3}{7}+1+\dfrac{3}{7}\)

=1

e: \(\dfrac{2}{-5}-\left(\dfrac{5}{2}-\dfrac{12}{5}\right)\)

\(=-\dfrac{2}{5}-\dfrac{5}{2}+\dfrac{12}{5}=2-\dfrac{5}{2}=-\dfrac{1}{2}\)

Bài 1:

a: \(\dfrac{1}{12}+\dfrac{3}{4}-\dfrac{5}{8}\)

\(=\dfrac{2}{24}+\dfrac{18}{24}-\dfrac{15}{24}=\dfrac{5}{24}\)

bài 2:

a: \(x-\dfrac{12}{3}=\dfrac{1}{3}\)

=>\(x=\dfrac{1}{3}+\dfrac{12}{3}=\dfrac{13}{3}\)

b: \(\left(2,8x-32\right):\dfrac{6}{3}=-30\)

=>\(2,8x-32=-30\cdot2=-60\)

=>2,8x=-28

=>x=-10

Bài 3:

a: Huyện B góp được \(\dfrac{5}{6}\cdot72=60\left(tấn\right)\)

Huyện C góp được \(60:\dfrac{4}{5}=75\left(tấn\right)\)

Cả ba huyện góp được: 72+60+75=207(tấn)

b: Tỉ số phần trăm giữa số rau ở huyện A và số rau ở huyện B là:

\(72:60=120\%\)

mong các bn giúp mình với ạ

9: \(A=\dfrac{3^2}{10}+\dfrac{3^2}{40}+...+\dfrac{3^2}{340}\)

\(=3\left(\dfrac{3}{10}+\dfrac{3}{40}+...+\dfrac{3}{340}\right)\)

\(=3\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+...+\dfrac{3}{17\cdot20}\right)\)

\(=3\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{17}-\dfrac{1}{20}\right)\)

\(=3\left(\dfrac{1}{2}-\dfrac{1}{20}\right)=3\cdot\dfrac{9}{20}=\dfrac{27}{20}\)

10: \(A=\dfrac{5^2}{1\cdot6}+\dfrac{5^2}{6\cdot11}+...+\dfrac{5^2}{26\cdot31}\)

\(=5\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{26\cdot31}\right)\)

\(=5\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{25}-\dfrac{1}{31}\right)\)

\(=5\left(1-\dfrac{1}{31}\right)=5\cdot\dfrac{30}{31}=\dfrac{150}{31}\)

11: \(A=\dfrac{6}{15}+\dfrac{6}{35}+\dfrac{6}{63}+\dfrac{6}{99}\)

\(=3\left(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+\dfrac{2}{99}\right)\)

\(=3\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}\right)\)

\(=3\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}\right)\)

\(=3\left(\dfrac{1}{3}-\dfrac{1}{11}\right)=3\cdot\dfrac{8}{33}=\dfrac{8}{11}\)

12: \(A=\dfrac{3}{3\cdot5}+\dfrac{3}{5\cdot7}+...+\dfrac{3}{49\cdot51}\)

\(=\dfrac{3}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{49\cdot51}\right)\)

\(=\dfrac{3}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=\dfrac{3}{2}\left(\dfrac{1}{3}-\dfrac{1}{51}\right)=\dfrac{3}{2}\cdot\dfrac{16}{51}=\dfrac{8}{17}\)

13: \(A=\dfrac{1}{2}+\dfrac{2}{2\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{4}{7\cdot11}+\dfrac{5}{11\cdot16}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}\)

\(=1-\dfrac{1}{16}=\dfrac{15}{16}\)

14: \(A=\dfrac{1}{2}+\dfrac{2}{8}+\dfrac{3}{28}+\dfrac{4}{77}+\dfrac{5}{176}\)

\(=\dfrac{1}{1\cdot2}+\dfrac{2}{2\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{4}{7\cdot11}+\dfrac{5}{11\cdot16}\)

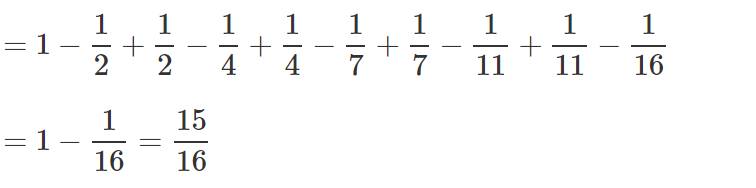
15: \(A=\dfrac{3}{54}+\dfrac{5}{126}+\dfrac{7}{294}+\dfrac{8}{609}\)

\(=\dfrac{3}{6\cdot9}+\dfrac{5}{9\cdot14}+\dfrac{7}{14\cdot21}+\dfrac{8}{21\cdot29}\)

\(=\dfrac{1}{6}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{21}+\dfrac{1}{21}-\dfrac{1}{29}\)

\(=\dfrac{1}{6}-\dfrac{1}{29}=\dfrac{23}{174}\)

16: \(A=\dfrac{5}{24}+\dfrac{5}{104}+\dfrac{5}{234}+\dfrac{5}{414}\)

\(=\dfrac{5}{3\cdot8}+\dfrac{5}{8\cdot13}+\dfrac{5}{13\cdot18}+\dfrac{5}{18\cdot23}\)

\(=\dfrac{1}{3}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{18}+\dfrac{1}{18}-\dfrac{1}{23}\)

\(=\dfrac{1}{3}-\dfrac{1}{23}=\dfrac{20}{69}\)

17: \(A=\dfrac{\dfrac{3}{54}+\dfrac{5}{126}+\dfrac{7}{294}}{\dfrac{5}{24}+\dfrac{5}{104}+\dfrac{5}{234}}\)

\(=\dfrac{\dfrac{1}{6}-\dfrac{1}{21}}{\dfrac{1}{3}-\dfrac{1}{18}}=\dfrac{15}{126}:\dfrac{15}{54}=\dfrac{54}{126}=\dfrac{3}{7}\)

\(A=\dfrac{5\cdot4^6\cdot9^4-3^9\cdot\left(-8\right)^4}{4\cdot2^{13}\cdot3^8+2\cdot8^4\cdot\left(-27\right)^3}\)

\(=\dfrac{5\cdot2^{12}\cdot3^8-3^9\cdot2^{12}}{2^{15}\cdot3^8-2^{13}\cdot3^9}\)

\(=\dfrac{2^{12}\cdot3^8\left(5-3\right)}{2^{13}\cdot3^8\left(2^2-3\right)}\)

\(=\dfrac{2^{13}}{2^{13}}=1\)

MỌI NGƯỜI GIÚP MK VS Ạ

 rảnh à

??????????????????????????

số học sinh của trường có thể là 280 hoặc 501.

Gọi số học sinh của trường là x(bạn)

(Điều kiện: \(x\in Z^+\))

Số học khi xếp hàng 13 thì dư 4 em nên \(x-4\in B\left(13\right)\)

=>\(x-4\in\left\{...;247;260;273;...;598;...\right\}\)

=>\(x\in\left\{...;251;264;277;...;602;...\right\}\)

mà 250<=x<=600

nên \(x\in\left\{251;264;277;...;589\right\}\left(1\right)\)

Số học sinh khi xếp hàng 17 thì dư 9 em nên \(x-9\in B\left(17\right)\)

=>\(x-9\in\left\{...;255;272;...;595;...\right\}\)

=>\(x\in\left\{...;264;281;...;604;...\right\}\)

mà 250<=x<=600

nên \(x\in\left\{264;281;...;587\right\}\left(2\right)\)

Số học sinh khi xếp hàng 5 thì vừa hết nên \(x\in B\left(5\right)\)

mà 250<=x<=600

nên \(x\in\left\{250;255;260;...;600\right\}\left(3\right)\)

Từ (1),(2),(3) suy ra 

\(\left\{{}\begin{matrix}x\in\left\{251;264;...;589\right\}\\x\in\left\{264;281;...;587\right\}\\x\in\left\{250;255;260;...;600\right\}\end{matrix}\right.\)

=>x=485

Vậy: Số học sinh là 485 bạn

1: \(\left(-12,5\right)+17,55+\left(-3,5\right)-\left(-2,45\right)\)

\(=\left(-12,5-3,5\right)+17,55+2,45\)

=-16+20

=4

2: \(\dfrac{-3}{5}\cdot\dfrac{2}{7}+2\dfrac{3}{5}-\dfrac{3}{5}\cdot\dfrac{5}{7}\)

\(=-\dfrac{3}{5}\left(\dfrac{2}{7}+\dfrac{5}{7}\right)+\dfrac{13}{5}\)

\(=-\dfrac{3}{5}+\dfrac{13}{5}=\dfrac{10}{5}=2\)

3: \(\dfrac{2}{3}:x=2,4-\dfrac{4}{5}\)

=>\(\dfrac{2}{3}:x=2,4-0,8=1,6\)

=>\(x=\dfrac{2}{3}:1,6=\dfrac{2}{4,8}=\dfrac{1}{2,4}=\dfrac{5}{12}\)