cmr: \(3^{1999}-7^{1997}⋮5\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TH1: p=3
\(p^2+2=3^2+2=11;p^3+2=3^3+2=29\)
=>Nhận
TH2: p=3k+1
\(p^2+2=\left(3k+1\right)^2+2=9k^2+6k+1+2\)
\(=9k^2+6k+3=3\left(3k^2+2k+1\right)⋮3\)
=>Loại
TH3: p=3k+2
\(p^2+2=\left(3k+2\right)^2+2=9k^2+12k+4+2\)
\(=9k^2+12k+6=3\left(3k^2+4k+2\right)⋮3\)
=>Loại

a: \(\left(\dfrac{7}{5}+\dfrac{-5}{11}\right)-\left(\dfrac{6}{11}-\dfrac{3}{5}\right)-2023^0\)
\(=\dfrac{7}{5}-\dfrac{5}{11}-\dfrac{6}{11}+\dfrac{3}{5}-1\)
\(=\dfrac{10}{5}-\dfrac{11}{11}-1=2-1-1=0\)
b: \(\dfrac{2}{9}\cdot\dfrac{7}{15}+\dfrac{2}{9}\cdot\dfrac{8}{15}+\dfrac{12}{3}\)
\(=\dfrac{2}{9}\left(\dfrac{7}{15}+\dfrac{8}{15}\right)+4=\dfrac{2}{9}+4=\dfrac{38}{9}\)
c: \(\dfrac{1}{3}+\dfrac{-7}{12}+\dfrac{2}{3}+\dfrac{-5}{12}\)
\(=\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(-\dfrac{7}{12}-\dfrac{5}{12}\right)\)
\(=\dfrac{3}{3}-\dfrac{12}{12}=1-1=0\)
d: \(\dfrac{3}{7}\cdot\dfrac{-9}{13}+\dfrac{3}{7}-\dfrac{4}{13}+\dfrac{13}{7}\)
\(=\dfrac{3}{7}\left(-\dfrac{9}{13}+1\right)-\dfrac{4}{13}+\dfrac{13}{7}\)
\(=\dfrac{3}{7}\cdot\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{13}{7}=\dfrac{4}{13}\cdot\dfrac{-4}{7}+\dfrac{13}{7}\)
\(=\dfrac{-16+169}{91}=\dfrac{153}{91}\)
e: \(\dfrac{2}{5}-\left(\dfrac{5}{2}-\dfrac{12}{5}\right)=\dfrac{2}{5}-\dfrac{5}{2}+\dfrac{12}{5}=\dfrac{14}{5}-\dfrac{5}{2}\)
\(=\dfrac{28-25}{10}=\dfrac{3}{10}\)

a: \(7,5\cdot1\dfrac{3}{4}-6\dfrac{2}{5}\)
\(=7,5\cdot1,75-6,4\)
=13,125-6,4
=6,725
b: \(6\dfrac{5}{12}:2\dfrac{3}{4}+11\dfrac{1}{4}\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{45}{4}\cdot\dfrac{2}{15}\)
\(=\dfrac{77}{12}\cdot\dfrac{4}{11}+\dfrac{3}{2}\)
\(=\dfrac{7}{3}+\dfrac{3}{2}=\dfrac{23}{6}\)


p là số nguyên tố lớn hơn 3
=>(p=3k+1 hoặc p=3k+2 ) và p lẻ
p lẻ nên p=2a+1
\(p^2-1=\left(2a+1\right)^2-1=\left(2a+1-1\right)\left(2a+1+1\right)\)
\(=2a\left(2a+2\right)=4a\left(a+1\right)\)
Vì a;a+1 là hai số nguyên liên tiếp
nên \(a\left(a+1\right)⋮2\)
=>\(4a\left(a+1\right)⋮4\cdot2=8\)
=>\(p^2-1⋮8\)(4)
TH1: p=3k+1
\(p^2-1=\left(3k+1-1\right)\left(3k+1+1\right)\)
\(=3k\left(3k+2\right)⋮3\)(1)
TH2: p=3k+2
\(p^2-1=\left(3k+2\right)^2-1\)
\(=\left(3k+2+1\right)\left(3k+2-1\right)\)
\(=\left(3k+3\right)\left(3k+1\right)=3\left(k+1\right)\left(3k+1\right)⋮3\left(2\right)\)
Từ (1),(2) suy ra \(p^2-1⋮3\left(3\right)\)
Từ (3),(4) suy ra \(p^2-1⋮BCNN\left(3;8\right)\)
=>\(p^2-1⋮24\)

Câu 1: B
Câu 2: D
Câu 3: B
Câu 4: C
Câu 5: A
Câu 6: B
Câu 7: C
Câu 8: B
Câu 9: C
Câu 10: D
Câu 11: D
Câu 12: C
Bài 1:
a: \(\dfrac{7}{30}+\dfrac{-12}{37}+\dfrac{23}{30}+\dfrac{-25}{37}\)
\(=\left(\dfrac{7}{30}+\dfrac{23}{30}\right)+\left(-\dfrac{12}{37}-\dfrac{25}{37}\right)\)
\(=\dfrac{30}{30}+\dfrac{-37}{37}=1-1=0\)
b: \(\dfrac{-20}{23}+\dfrac{8}{15}-\dfrac{3}{23}+\dfrac{7}{15}+\dfrac{1}{2}\)
\(=\left(-\dfrac{20}{23}-\dfrac{3}{23}\right)+\left(\dfrac{8}{15}+\dfrac{7}{15}\right)+\dfrac{1}{2}\)
\(=-1+1+\dfrac{1}{2}=\dfrac{1}{2}\)
c: \(\left(-12,5\right)+17,55+\left(-3,5\right)+2,45\)
\(=\left(-12,5-3,5\right)+\left(17,55+2,45\right)\)
=20-16
=4
d: \(\left(-9,237\right)+3,8+1,237-3,8+1,123\)
\(=\left(-9,237+1,237\right)+\left(3,8-3,8\right)+1,123\)
=-8+1,123
=-6,877
e: \(4,35-\left(2,67-1,65\right)+\left(3,54-6,33\right)\)
\(=4,35-2,67+1,65+3,54-6,33\)
\(=6-9+3,54=3,54-3=0,54\)
g: \(\dfrac{5}{7}\cdot\dfrac{5}{11}+\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\)
\(=\dfrac{5}{7}\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)=\dfrac{5}{7}\cdot\dfrac{-7}{11}=-\dfrac{5}{11}\)
h: \(\dfrac{-5}{7}\cdot\dfrac{3}{13}+\dfrac{-5}{7}\cdot\dfrac{10}{13}+1\dfrac{5}{7}\)
\(=-\dfrac{5}{7}\left(\dfrac{3}{13}+\dfrac{10}{13}\right)+\dfrac{12}{7}=-\dfrac{5}{7}+\dfrac{12}{7}=\dfrac{7}{7}=1\)
i: \(3,58\cdot24,45+3,58\cdot75,55+12,42\)
\(=3,58\left(24,45+75,55\right)+12,42\)
\(=358+12,42=370,42\)
k: \(3,4\cdot\left(-23,68\right)-3,4\cdot45,12+\left(-31,2\right)\cdot3,4\)
\(=3,4\left(-23,68-45,12-31,2\right)\)
\(=3,4\cdot\left(-100\right)=-340\)
l: \(1,14\cdot6,4+1,14\cdot3,6+11,4\)
\(=1,14\left(6,4+3,6\right)+1,14\cdot10\)
\(=1,14\cdot20=22,8\)

Nửa chu vi hình chữ nhật là 18:2=9(cm)
Chu vi không đổi thì nửa chu vi cũng không đổi
Tỉ số giữa chiều dài mới so với chiều dài cũ là:
100%-20%=0,8
Tỉ số giữa chiều rộng mới so với chiều rộng cũ là:
25%+100%=125%=1,25
0,8xchiềudài+1,25x chiều rộng=9
=>chiều dài+1,5625 chiều rộng=11,25
mà chiều dài+chiều rộng=9
nên 0,5625 lần chiều rộng là 11,25-9=2,25
=>Chiều rộng là 2,25:0,5625=4(cm)
=>Chiều dài là 9-4=5(cm)
Diện tích hình chữ nhật là \(5\cdot4=20\left(cm^2\right)\)


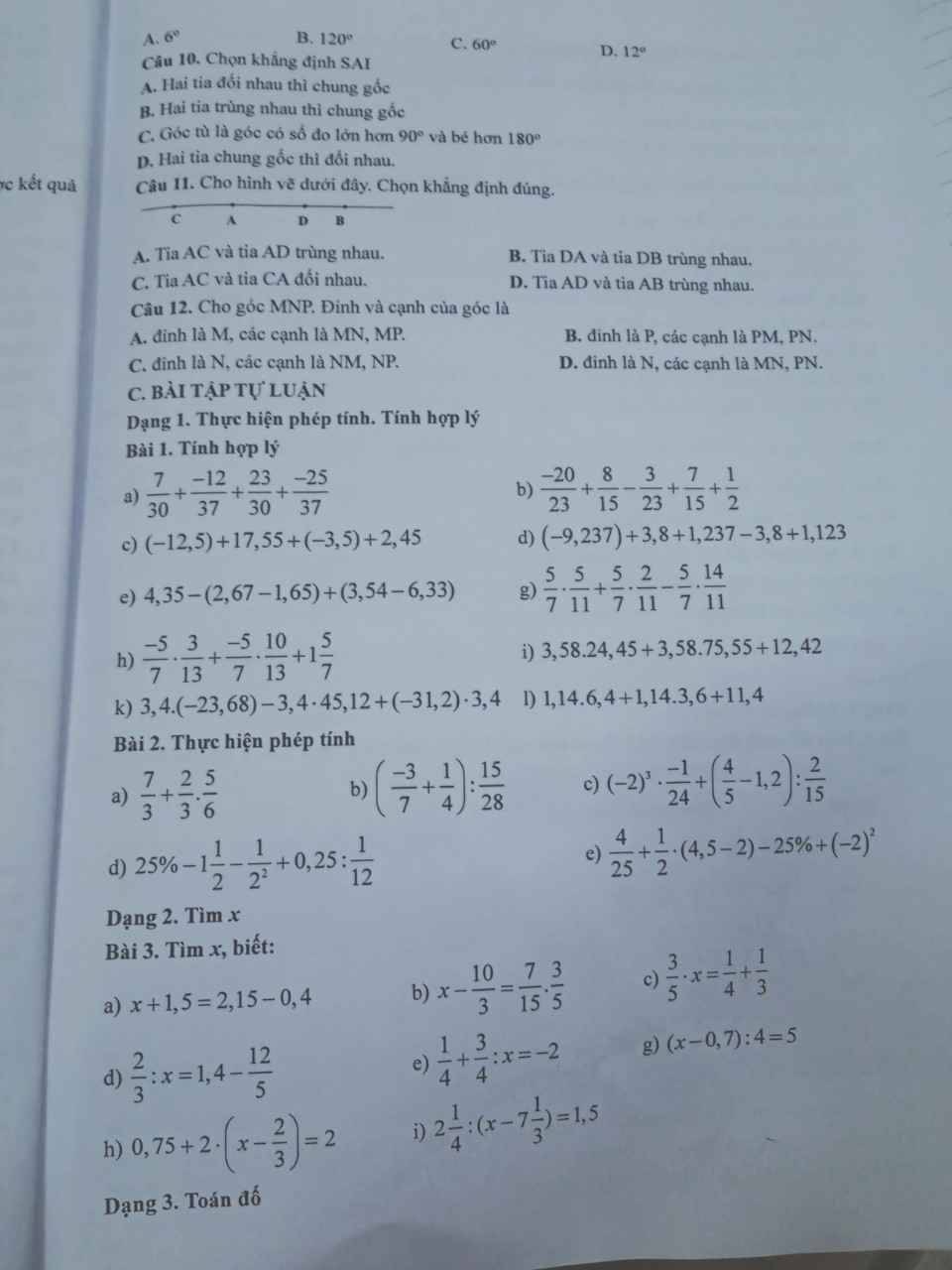
\(=3^3.3^{1996}+7.7^{1996}=3^3.\left(3^4\right)^{499}+7.\left(7^4\right)^{499}\)
Ta có
\(3^4\) có tận cùng là 1 => \(\left(3^4\right)^{499}\) có tận cùng là 1
=> \(3^3.\left(3^4\right)^{499}=27.\left(3^4\right)^{499}\) có tận cùng là 7
\(7^4\) có tận cùng là 1 => \(\left(7^4\right)^{499}\) có tận cùng là 1
=> \(7.\left(7^4\right)^{499}\) có tận cùng là 1 =>
\(\Rightarrow3^{1999}-7^{1997}\) có tận cùng là 0 \(\Rightarrow3^{1999}-7^{1997}⋮5\)