cho tam giác ABC cân tại A có M là trung điểm của BC từ M kẻ MH vuông góc với AB ,MK vuông góc với AC.a) CM tam giác MHB=tam giác MKC b) CM tam giác MHA=tam giác MKA.giúp mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y = k/x (k khác 0)
<=> x = k/y (k khác 0)
Chúc bạn học tốt nhé


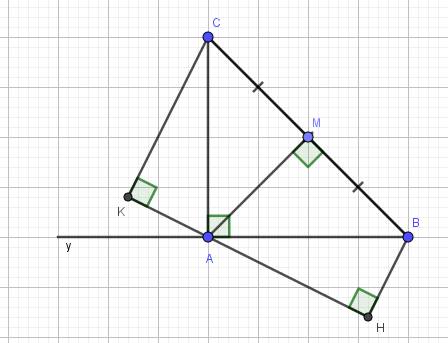
a) Xét hai tam giác vuông:\(\Delta AMB\) và \(\Delta AMC\) có:
\(BM=MC\left(gt\right)\)
AM là cạnh chung
\(\Rightarrow\Delta AMB=\Delta AMC\) (hai cạnh góc vuông)
\(\Rightarrow AB=AC\) (hai cạnh tương ứng)
b) Vẽ tia đối của tia AB là tia Ay
Ta có:
\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow AC\perp Ay\)
\(\Rightarrow\widehat{yAK}+\widehat{KAC}=90^0\)
Lại có:
\(\widehat{yAK}=\widehat{BAH}\) (đối đỉnh)
\(\Rightarrow\widehat{BAH}+\widehat{KAC}=90^0\)
Mà \(\widehat{ACK}+\widehat{KAC}=90^0\) (\(\Delta ACK\) vuông tại K)
\(\Rightarrow\widehat{BAH}=\widehat{ACK}\)
Do \(\Delta AMB=\Delta AMC\left(cmt\right)\)
\(\Rightarrow AB=AC\) (hai cạnh tương ứng)
Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CKA\) có:
\(AB=AC\left(cmt\right)\)
\(\widehat{BAH}=\widehat{ACK}\left(cmt\right)\)
\(\Rightarrow\Delta AHB=\Delta CKA\) (cạnh huyền - góc nhọn)

Lời giải:
Xét tam giác $ABD$ và $AED$ có:
$AB=AE$ (gt)
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là tia phân giác $\widehat{A}$)
$AD$ chung
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
$\Rightarrow BD=ED$ (đpcm)


a) Xét hai tam giác vuông: ∆BDF và ∆EDC có:
BD = ED (gt)
∠BDF = ∠EDC (đối đỉnh)
⇒ ∆BDF = ∆EDC (cạnh góc vuông - góc nhọn kề)
b) Do ∆BDF = ∆EDC (cmt)
⇒ ∠BFD = ∠ECD (hai góc tương ứng)
⇒ ∠F = ∠C
c) Do ∆BDF = ∆EDC (cmt)
⇒ DF = DC (hai cạnh tương ứng)
Ta có:
EF = DE + DF
BC = BD + DC
Mà DE = BD (gt)
DF = DC (cmt)
⇒ EF = BC
Xét hai tam giác vuông: ∆AEF và ∆ABC có
EF = BC (cmt)
∠F = ∠C (cmt)
⇒ ∆AEF = ∆ABC (cạnh góc vuông - góc nhọn kề)

Sĩ số của lớp 7A là: \(15+14+10+6=45\) nên số phần tử của không gian mẫu chính là số cách chọn 5 bạn trong 45 bạn.
Bạn đầu tiên có 45 cách chọn, bạn thứ hai có 44 cách chọn,..., bạn thứ năm sẽ có 41 cách chọn \(\Rightarrow\) Có \(45.44.43.42.41\) cách chọn ra nhóm 5 bạn, nhưng vì theo cách chọn trên, mỗi nhóm 5 bạn sẽ bị lặp lại \(1.2.3.4.5=120\) lần nên có tất cả \(\dfrac{45.44.43.42.41}{120}=1221759\) hay \(n\left(\Omega\right)=1221759\)
Gọi A là biến cố: "Trong nhóm 5 bạn được chọn có đủ các dân tộc H' Mông, Mường, Tày, Thái."
Ta thấy có các TH sau xảy ra:
TH1: Trong 5 bạn có 2 bạn của dân tộc H'Mông: Có \(15.14.14.10.6\) cách. Nhưng khi đó mỗi nhóm sẽ bị tính 120 lần (như trên) nên có tất cả \(\dfrac{15.14.14.10.6}{120}=1470\) cách chọn nhóm.
TH2: Trong 5 bạn có 2 bạn của dân tộc Mường thì tương tự, có \(\dfrac{15.14.13.10.6}{120}=1365\) cách chọn nhóm.
TH3: Trong 5 bạn có 2 bạn của dân tộc Tày: Có \(\dfrac{15.14.10.9.6}{120}=945\) cách chọn nhóm.
TH4: Trong 5 bạn có 2 bạn của dân tộc Thái: Có \(\dfrac{15.14.10.6.5}{120}=525\) cách chọn nhóm
\(\Rightarrow n\left(A\right)=1470+945+1365+525=4305\)
\(\Rightarrow P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4305}{1221759}=\dfrac{5}{1419}\)

Lời giải:
a. Xét tam giác $MHB$ và $MKC$ có:
$\widehat{MHB}=\widehat{MKC}=90^0$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{MBH}=\widehat{MCK}$ (do $ABC$ cân tại $A$)
$\Rightarrow \triangle MHB=\triangle MKC$ (ch-gn)
b.
Xét tam giác $MHA$ và $MKA$ có:
$MA$ chung
$\widehat{MHA}=\widehat{MKA}=90^0$
$MH=MK$ (hệ quả từ $\triangle MHB=\triangle MKC$ phần a)
$\Rightarrow \triangle MHA=\triangle MKA$ (ch-cgv)
Hình vẽ: