a; A = (1.2 + 2.3 + 3.4+ ... + 19.20)(13 - 3).(13 - 4)...(13 - 20)

 A =(1.2 + 2.3 + 3.4 + ... + 19.20).(13 - 3).(13 - 4)...(13 - 13)...(13 - 20)

A = (1.2 + 2.3 + 3.4 + ... + 19.20).(13 - 3).(13 - 4)...0...(13 - 20)

A = 0

a; A = (1.2 + 2.3 + 3.4+ ... + 19.20)(13 - 3).(13 - 4)...(13 - 20)

 A =(1.2 + 2.3 + 3.4 + ... + 19.20).(13 - 3).(13 - 4)...(13 - 13)...(13 - 20)

A = (1.2 + 2.3 + 3.4 + ... + 19.20).(13 - 3).(13 - 4)...0...(13 - 20)

A = 0

Chúc bạn học tốt !!!!

\(H=4x^2+4x+5\\=(4x^2+4x+1)+4\\=(2x+1)^2+4\)

Ta thấy: \(\left(2x+1\right)^2\ge0\forall x\)

\(\Rightarrow\left(2x+1\right)^2+4\ge4\forall x\Rightarrow H\ge4\forall x\)

Dấu \("="\) xảy ra khi: \(2x+1=0\Leftrightarrow x=-\dfrac{1}{2}\)

Vậy \(Min_H=4\) tại \(x=-\dfrac{1}{2}\).

a-b=7 nên a=b+7

\(\dfrac{3a-b}{2a+7}+\dfrac{3b-a}{2b-7}\)

\(=\dfrac{3\left(b+7\right)-b}{2\left(b+7\right)+7}+\dfrac{3b-b-7}{2b-7}\)

\(=\dfrac{2b+21}{2b+21}+\dfrac{2b-7}{2b-7}=1+1=2\)

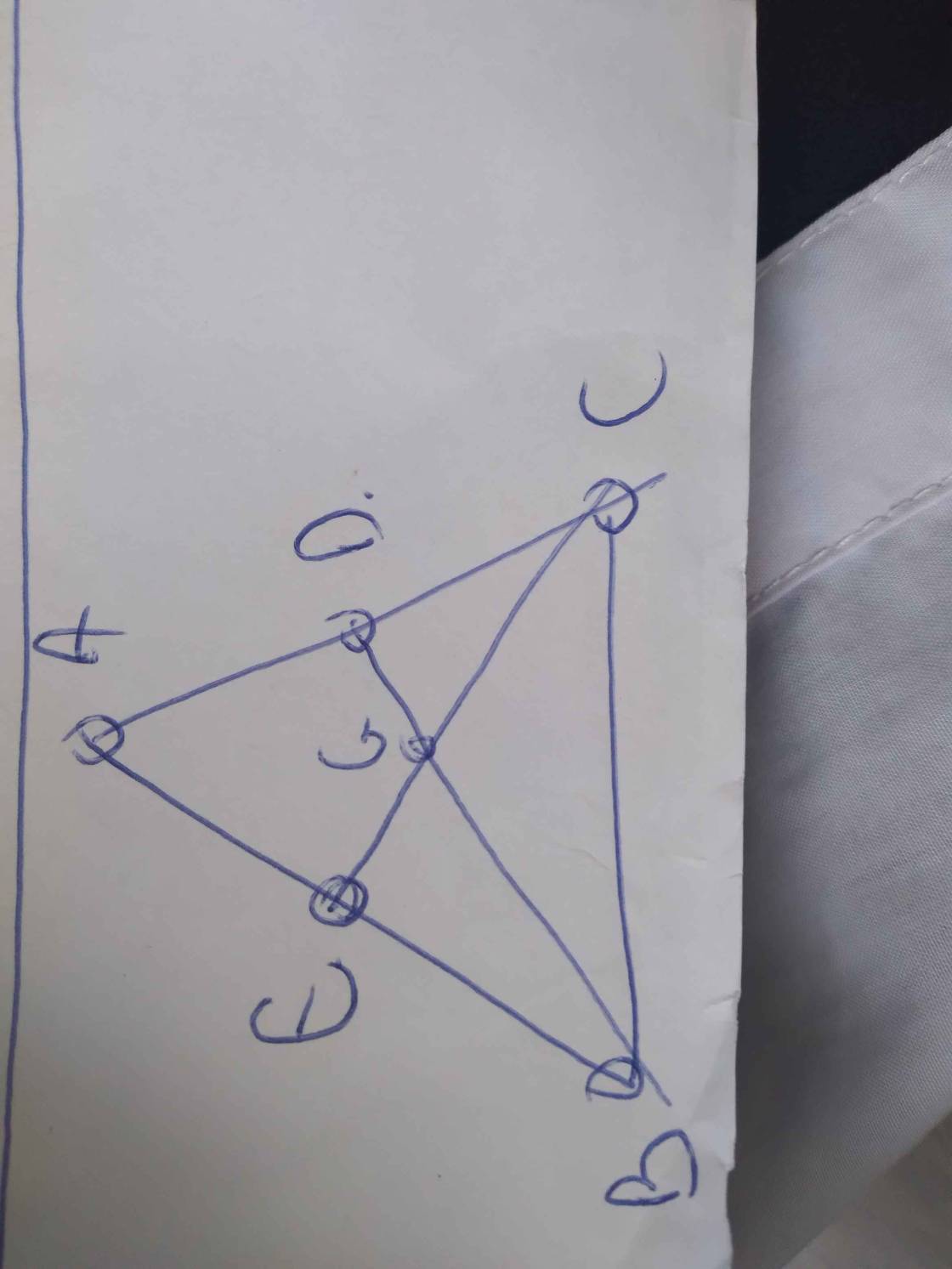
a: Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến

nên MA=MB=MC=CB/2

\(\widehat{KAB}+\widehat{BAC}+\widehat{CAI}=180^0\)

=>\(\widehat{CAI}+90^0+45^0=180^0\)

=>\(\widehat{CAI}=45^0\)

Xét ΔKBA vuông tại K có \(\widehat{KAB}=45^0\)

nên ΔKAB vuông cân tại K

=>KA=KB

Xét ΔIAC vuông tại I có \(\widehat{IAC}=45^0\)

nên ΔIAC vuông cân tại I

=>IA=IC

Ta có: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: KA=KB

=>K nằm trên đường trung trực của AB(2)

Từ (1) và (2) suy ra MK là đường trung trực của AB

Ta có: MA=MC

=>M nằm trên đường trung trực của AC(3)

ta có: IA=IC

=>I nằm trên đường trung trực của AC(4)

Từ (3),(4) suy ra MI là đường trung trực của AC

b: Gọi H là giao điểm của MK với AB, F là giao điểm của MI với AC

MK là đường trung trực của AB

mà H là giao của MK với AB nên MK\(\perp\)AB tại H

MI là đường trung trực của AC

mà F là giao của MI với AC nên MI\(\perp\)AC tại F

Xét tứ giác AHMF có

\(\widehat{AHM}=\widehat{AFM}=\widehat{HAF}=90^0\)

nên AHMF là hình chữ nhật

=>\(\widehat{FMH}=90^0\)

=>\(\widehat{IMK}=90^0\)

Cửa Nam thành Tây Đô được xây vào năm 1397

\(M=5x\left(x-1\right)-4x\left(x-5\right)-\dfrac{11}{20}\)

\(=5x^2-5x-4x^2+20x-\dfrac{11}{20}=x^2+15x-\dfrac{11}{20}\)

Khi x=2 thì \(M=2^2+15\cdot2-\dfrac{11}{20}=\dfrac{669}{20}\)

\(N=\left(x-3\right)\left(x+7\right)-\left(2x-5\right)\left(x-1\right)\)

\(=x^2+4x-21-2x^2+7x-5\)

\(=-x^2+11x-26\)

Khi x=0 thì \(N=-0^2+11\cdot0-26=-26\)

Thay x=1 vào N, ta được:

\(N=-1^2+11\cdot1-26=-1+11-26=-27+11=-16\)

Khi x=-1 thì \(N=-\left(-1\right)^2+11\cdot\left(-1\right)-26=-1-11-26=-38\)