Tổ một trồng hơn tổ hai 15 cây .tính số cây mỗi tổ trồng được biết số cây tổ hai trồng bằng 1/4 số cây tổ một
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: \(B=\left(1+\dfrac{1}{1\cdot3}\right)\cdot\left(1+\dfrac{1}{2\cdot4}\right)\cdot...\cdot\left(1+\dfrac{1}{2022\cdot2024}\right)\)
\(=\left(1+\dfrac{1}{2^2-1}\right)\cdot\left(1+\dfrac{1}{3^2-1}\right)\cdot...\cdot\left(1+\dfrac{1}{2023^2-1}\right)\)
\(=\dfrac{2^2}{2^2-1}\cdot\dfrac{3^2}{3^2-1}\cdot...\cdot\dfrac{2023^2}{2023^2-1}\)
\(=\dfrac{2\cdot3\cdot...\cdot2023}{1\cdot2\cdot...\cdot2022}\cdot\dfrac{2\cdot3\cdot....\cdot2023}{3\cdot4\cdot...\cdot2024}\)
\(=\dfrac{2023}{1}\cdot\dfrac{2}{2024}=\dfrac{2023}{1012}\)

xy-3x-2y+1=0
x(y-3)-2y+1=0
2x(y-3)-4y+2=0
2x(y-3)-4y+2+10-10=0
2x(y-3)-4y+12=0+10
2x(y-3)-4(y-3)=10
(y-3)(2x-4)=10
10=1.10=2.5=(-1)(-10)=(-2)(-5)
Vì 2x-4 là số chẵn
Ta có bảng:
| y-3 | 1 | 5 | -1 | -5 |
| y | 4 | 8 | 2 | -2 |
| 2x-4 | 10 | 2 | -10 | -2 |
| 2x | 14 | 6 | -6 | 2 |
| x | 7 | 3 | -3 | 1 |
Vậy (x;y)ϵ{(7;4);(3;8);(-3;2);(1;-2)}


Số số hạng của B:
2010 - 1 + 1 = 2010 (số hạng)
Do 2010 ⋮ 2 và 2010 ⋮ 3 nên ta có thể nhóm các số hạng của B thành các nhóm có 2 số hạng và 3 số hạng như sau:
B = 3 + 3² + 3³ + 3⁴ + ... + 3²⁰¹⁰
= (3 + 3²) + (3³ + 3⁴) + ... + (3²⁰⁰⁹ + 3²⁰¹⁰)
= 3(1 + 3) + 3³(1 + 3) + ... + 3²⁰⁰⁹(1 + 3)
= 3.4 + 3³.4 + ... + 3²⁰⁰⁹.4
= 4.(3 + 3³ + ... + 3²⁰⁰⁹) ⋮ 4
B = 3 + 3² + 3³ + 3⁴ + ... + 3²⁰¹⁰
= (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) + ... + (3²⁰⁰⁸ + 3²⁰⁰⁹ + 3²⁰¹⁰)
= 3(1 + 3 + 3²) + 3⁴(1 + 3 + 3²) + ... + 3²⁰⁰⁸(1 + 3 + 3²)
= 3.13 + 3⁴.13 + ... + 3²⁰⁰⁸.13
= 13.(3 + 3⁴ + ... + 3²⁰⁰⁸) ⋮ 13
Vậy B ⋮ 4 và B ⋮ 13

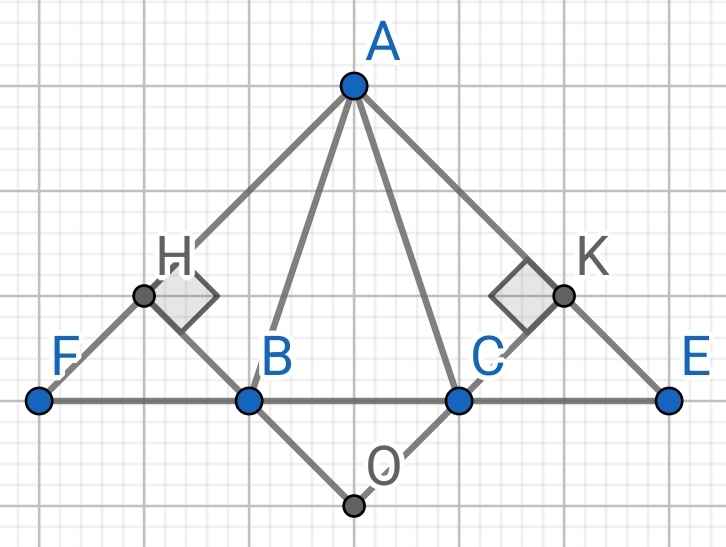
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB
Ta có:
∠ABF + ∠ABC = 180⁰ (kề bù)
∠ACE + ∠ACB = 180⁰ (kề bù)
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABF = ∠ACE
Xét ∆ABF và ∆ACE có:
AB = AC (cmt)
∠ABE = ∠ACF (cmt)
BF = CE (gt)
⇒ ∆ABF = ∆ACE (c-g-c)
⇒ AF = AE (hai cạnh tương ứng)
⇒ ∆AEF cân tại A
b) *) Cách 1:
Do ∆ABF = ∆ACE (cmt)
⇒ ∠BAF = ∠CAE (hai góc tương ứng)
⇒ ∠BAH = ∠CAK
Xét hai tam giác vuông: ∆ABH và ∆ACK có:
AB = AC (cmt)
∠BAH = ∠CAK (cmt)
⇒ ∆ABH = ∆ACK (cạnh huyền - góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
*) Cách 2:
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF
⇒ ∠HFB = ∠KEC
Xét hai tam giác vuông: ∆BHF và ∆CKE có:
BF = CE (gt)
∠HFB = ∠KEC (cmt)
⇒ ∆BHF = ∆CKE (cạnh huyền - góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
c) Sửa đề: Gọi O là giao điểm của HB và KC
Do ∆BHF = ∆CKE (cmt)
⇒ ∠HBF = ∠KCE (hai góc tương ứng)
Mà ∠CBO = ∠HBF (đối đỉnh)
∠BCO = ∠KCE (đối đỉnh)
⇒ ∠CBO = ∠BCO
⇒ ∆BOC cân tại O

`#3107.101107`
\(106-\left(x+7\right)=9\\ \Rightarrow x+7=106-9\\ \Rightarrow x+7=97\\ \Rightarrow x=97-7\\ \Rightarrow x=90\)
Vậy, `x = 90`
___
\(45-\left(x+10\right)=31\\ \Rightarrow x+10=45-31\\ \Rightarrow x+10=14\\ \Rightarrow x=14-10\\ \Rightarrow x=4\)
Vậy, `x = 4`
___
\(156-\left(x+61\right)=82\\ \Rightarrow x+61=156-82\\ \Rightarrow x+61=74\\ \Rightarrow x=74-61\\ \Rightarrow x=13\)
Vậy, `x = 13`
___
\(126-\left(x+32\right)=86\\ \Rightarrow x+32=126-86\\ \Rightarrow x+32=40\\ \Rightarrow x=40-32\\ \Rightarrow x=8\)
Vậy, `x = 8.`

`#3107.101107`
`a)`
\(187+x=320\\ \Rightarrow x=320-187\\ \Rightarrow x=133\)
Vậy, `x = 133`
`b)`
\(765-x=158\\ \Rightarrow x=765-158\\ \Rightarrow x=607\)
Vậy, `x = 607`
`c)`
\(451+\left(x-218\right)=876\\ \Rightarrow x-218=876-451\\ \Rightarrow x-218=425\\ \Rightarrow x=425-218\\ \Rightarrow x=207\)
Vậy, `x = 207.`

a, \(1339:x=13\Leftrightarrow x=\dfrac{1339}{13}=103\)
b, \(1428:x=14\Leftrightarrow x=\dfrac{1428}{14}=102\)
c, \(2436:x=12\Leftrightarrow x=\dfrac{2436}{12}=203\)
a) 1339 : x = 13
x = 1339 : 13
x = 103
b) 1428 : x = 14
x = 1428 : 14
x = 102
c) 2436 : x = 12
x = 2436 : 12
x = 203
Hiệu số phần bằng nhau là 4-1=3(phần)
Số cây tổ một trồng được là:
15:(4-1)x4=20(cây)
Số cây tổ hai trồng được là: 20-15=5(cây)