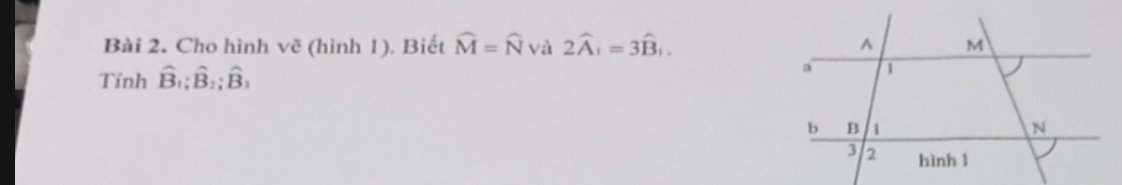
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left(x+2y\right)^2+\left(2x-y\right)^2-5\left(x+y\right)\left(x-y\right)-10\left(y+3\right)\left(y-3\right)\)
\(=x^2+4xy+4y^2+4x^2-4xy+y^2-5\left(x^2-y^2\right)-10\left(y^2-9\right)\)
\(=5x^2+5y^2-5x^2+5y^2-10y^2+90\)
=90
=>A không phụ thuộc vào biến

a: \(\dfrac{3x+5}{2}-x>=1+\dfrac{x+2}{3}\)
=>\(\dfrac{3x+5-2x}{2}>=\dfrac{3+x+2}{3}\)
=>\(\dfrac{x+5}{2}-\dfrac{x+5}{3}>=0\)
=>\(\dfrac{3\left(x+5\right)-2\left(x+5\right)}{6}>=0\)
=>\(\dfrac{x+5}{6}>=0\)
=>x+5>=0
=>x>=-5
b: \(\dfrac{x-2}{3}-x-2< =\dfrac{x-17}{2}\)
=>\(\dfrac{2\left(x-2\right)}{6}+\dfrac{6\left(-x-2\right)}{6}< =\dfrac{3\left(x-17\right)}{6}\)
=>\(2\left(x-2\right)+6\left(-x-2\right)< =3\left(x-17\right)\)
=>\(2x-4-6x-12< =3x-51\)
=>-4x-16<=3x-51
=>-7x<=-35
=>x>=5
c: \(\dfrac{2x+1}{3}-\dfrac{x-4}{4}< =\dfrac{3x+1}{6}-\dfrac{x-4}{12}\)
=>\(\dfrac{4\left(2x+1\right)-3\left(x-4\right)}{12}< =\dfrac{2\left(3x+1\right)-x+4}{12}\)
=>4(2x+1)-3(x-4)<=2(3x+1)-x+4
=>8x+4-3x+12<=6x+2-x+4
=>5x+16<=5x+6
=>16<=6(sai)
Vậy: BPT vô nghiệm

a: \(\dfrac{3\left(2x+1\right)}{20}+1>\dfrac{3x+52}{10}\)
=>\(\dfrac{6x+3}{20}+\dfrac{20}{20}>\dfrac{6x+104}{20}\)
=>6x+23>6x+104
=>23>104(sai)
vậy: \(x\in\varnothing\)
b: \(\dfrac{4x-1}{2}+\dfrac{6x-19}{6}< =\dfrac{9x-11}{3}\)
=>\(\dfrac{3\left(4x-1\right)+6x-19}{6}< =\dfrac{2\left(9x-11\right)}{6}\)
=>12x-3+6x-19<=18x-22
=>-22<=-22(luôn đúng)
Vậy: \(x\in R\)

a: ĐKXĐ: \(x\notin\left\{1;-1;\dfrac{1}{2}\right\}\)
\(A=\left(\dfrac{1}{1-x}+\dfrac{2}{x+1}-\dfrac{5-x}{1-x^2}\right):\dfrac{1-2x}{x^2-1}\)
\(=\left(\dfrac{-1}{x-1}+\dfrac{2}{x+1}-\dfrac{x-5}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2x+1}\)
\(=\dfrac{-\left(x+1\right)+2\left(x-1\right)-x+5}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2x+1}\)
\(=\dfrac{-x-1+2x-2-x+5}{-2x+1}=\dfrac{2}{-2x+1}\)
b: Để A>0 thì \(\dfrac{2}{-2x+1}>0\)
mà 2>0
nên -2x+1>0
=>-2x>-1
=>\(x< \dfrac{1}{2}\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< \dfrac{1}{2}\\x\ne-1\end{matrix}\right.\)

a: \(x^2-3x+1>2\left(x-1\right)-x\left(3-x\right)\)
=>\(x^2-3x+1>2x-2-3x+x^2\)
=>-3x+1>-x-2
=>-2x>-3
=>\(x< \dfrac{3}{2}\)
b: \(\left(x-1\right)^2+x^2< =\left(x+1\right)^2+\left(x+2\right)^2\)
=>\(x^2-2x+1+x^2< =x^2+2x+1+x^2+4x+4\)
=>-2x+1<=6x+5
=>-7x<=4
=>\(x>=-\dfrac{4}{7}\)
c:
\(\left(x^2+1\right)\left(x-6\right)< =\left(x-2\right)^3\)
=>\(x^3-6x^2+x-6< =x^3-6x^2+12x-8\)
=>x-6<=12x-8
=>-11x<=-8+6=-2
=>\(x>=\dfrac{2}{11}\)

ĐKXĐ: \(x\ne1\)
c: Để A>1 thì \(A-1>0\)
=>\(\dfrac{x^2-x+1}{x-1}-1>0\)
=>\(\dfrac{x^2-x+1-x+1}{x-1}>0\)
=>\(\dfrac{x^2-2x+2}{x-1}>0\)
mà \(x^2-2x+2=\left(x-1\right)^2+1>=1>0\forall x\)
nên x-1>0
=>x>1
d: Để A nguyên thì \(x^2-x+1⋮x-1\)
=>\(x\left(x-1\right)+1⋮x-1\)
=>\(1⋮x-1\)
=>\(x-1\in\left\{1;-1\right\}\)
=>\(x\in\left\{2;0\right\}\)
Để giải các bài toán liên quan đến hàm số \[ A = \frac{x^2 - x + 1}{x - 1}, \] ta cần phân tích hàm số này.
### 1. Tìm điều kiện để \( A > 1 \)
Để tìm các giá trị của \( x \) sao cho \( A > 1 \), ta sẽ làm theo các bước sau:
1. **Biến đổi hàm số**:
\[
A = \frac{x^2 - x + 1}{x - 1}
\]
Ta phân tích phân thức này bằng cách chia \( x^2 - x + 1 \) cho \( x - 1 \) bằng phép chia đa thức:
**Chia \( x^2 - x + 1 \) cho \( x - 1 \):**
- Chia \( x^2 \) cho \( x \) được \( x \).
- Nhân \( x \) với \( x - 1 \) được \( x^2 - x \).
- Trừ \( x^2 - x \) khỏi \( x^2 - x + 1 \) ta còn dư \( 1 \).
Vậy,
\[
\frac{x^2 - x + 1}{x - 1} = x + \frac{2}{x - 1}
\]
2. **Đặt điều kiện \( A > 1 \)**:
\[
x + \frac{2}{x - 1} > 1
\]
- Trừ 1 từ cả hai vế:
\[
x + \frac{2}{x - 1} - 1 > 0
\]
- Kết hợp các hạng tử:
\[
x - 1 + \frac{2}{x - 1} > 0
\]
- Đặt \( t = x - 1 \), ta có:
\[
t + \frac{2}{t} > 0
\]
- Phân tích bất phương trình:
\[
t^2 + 2 > 0
\]
Vì \( t^2 + 2 \) luôn dương (bất kể giá trị của \( t \)), bất phương trình luôn đúng với mọi giá trị của \( t \neq 0 \). Do đó, điều kiện để \( A > 1 \) là \( x \neq 1 \).
### 2. Tìm giá trị nguyên của \( x \) sao cho \( A \) là số nguyên
1. **Biến đổi hàm số**:
\[
A = x + \frac{2}{x - 1}
\]
Để \( A \) là số nguyên, thì \(\frac{2}{x - 1}\) phải là số nguyên. Điều này có nghĩa là \( x - 1 \) phải là một ước của 2.
2. **Tìm các ước của 2**:
- Các ước của 2 là \( \pm 1, \pm 2 \).
3. **Tìm các giá trị tương ứng của \( x \)**:
- Nếu \( x - 1 = 1 \), thì \( x = 2 \).
- Nếu \( x - 1 = -1 \), thì \( x = 0 \).
- Nếu \( x - 1 = 2 \), thì \( x = 3 \).
- Nếu \( x - 1 = -2 \), thì \( x = -1 \).
4. **Kiểm tra các giá trị**:
- Với \( x = 2 \):
\[
A = \frac{2^2 - 2 + 1}{2 - 1} = \frac{3}{1} = 3
\]
- Với \( x = 0 \):
\[
A = \frac{0^2 - 0 + 1}{0 - 1} = \frac{1}{-1} = -1
\]
- Với \( x = 3 \):
\[
A = \frac{3^2 - 3 + 1}{3 - 1} = \frac{7}{2} = 3.5
\]
(Không phải là số nguyên)
- Với \( x = -1 \):
\[
A = \frac{(-1)^2 - (-1) + 1}{-1 - 1} = \frac{3}{-2} = -1.5
\]
(Không phải là số nguyên)
### Kết quả:
- **Điều kiện để \( A > 1 \)** là \( x \neq 1 \).
- **Các giá trị nguyên của \( x \) để \( A \) là số nguyên** là \( x = 0 \) và \( x = 2 \).

a: ĐKXĐ: \(x\ne-1\)
\(x^2+x=0\)
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Khi x=0 thì \(A=\dfrac{0-3}{0+1}=\dfrac{-3}{1}=-3\)
b: \(Q=A\cdot B\)
\(=\dfrac{x-3}{x+1}\left(\dfrac{3}{x-3}-\dfrac{6x}{9-x^2}+\dfrac{x}{x+3}\right)\)
\(=\dfrac{x-3}{x+1}\left(\dfrac{3\left(x+3\right)+6x+x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\right)\)
\(=\dfrac{x-3}{x+1}\cdot\dfrac{3x+9+6x+x^2-3x}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{1}{x+1}\cdot\dfrac{x^2+6x+9}{x+3}=\dfrac{x+3}{x+1}\)

a: Vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>AB=OA+OB=6+2=8(cm)
b: I là trung điểm của AB
=>\(IA=IB=\dfrac{AB}{2}=4\left(cm\right)\)
Vì AI<AO
nên I nằm giữa A và O
=>AI+IO=AO
=>IO+4=6
=>IO=2(cm)
=>OA=3IO
c: Các góc đỉnh O có trên hình là \(\widehat{xOt};\widehat{xOz};\widehat{xOy};\widehat{tOz};\widehat{tOy};\widehat{zOy}\)


Ta có: \(\widehat{M}=\widehat{N}\)
=>AM//BN
Ta có: AM//BN
=>\(\widehat{A_1}+\widehat{B_1}=180^0\)
mà \(2\widehat{A_1}=3\cdot\widehat{B_1}\)
nên \(\widehat{B_1}=180^0\cdot\dfrac{2}{5}=72^0\)
Ta có: \(\widehat{B_1}+\widehat{B_2}=180^0\)(hai góc kề bù)
=>\(\widehat{B_2}+72^0=180^0\)
=>\(\widehat{B_2}=108^0\)
\(\widehat{B_3}=\widehat{B_1}\)(hai góc đối đỉnh)
mà \(\widehat{B_1}=72^0\)
nên \(\widehat{B_3}=72^0\)