Ta thấy \(10^2!=100!=1.2.3...100\) nên có chữ số tận cùng là 0.

số 0

\(\left(2x+3\sqrt{x}-3\right)^2=116^2\)
\(\Leftrightarrow2x+3\sqrt{x}-3=116\)
Đặt \(\sqrt{x}=t\left(t\ge0\right)\)
\(\Rightarrow\)\(2t^2+3t-3=116\)
\(2t^2+3t-119=0\)
\(\Delta=3^2-4.2.\left(-119\right)\)\(=961\)
\(\Rightarrow\sqrt{\Delta}=\sqrt{961}=31\)\(>0\)
\(\Rightarrow\)hpt có 2 nghiệm phân biệt

\(\Rightarrow t_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-3+31}{2.2}=7\left(TM\right)\)
\(\Rightarrow t_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-3-31}{2.2}=\dfrac{-17}{2}\left(L\right)\)
Với \(t_1=7\Rightarrow\sqrt{x}=7\Leftrightarrow x=49\)
                        Vậy hpt có nghiệm là x = 49

\(\left(2x+3\sqrt{x}-3\right)^2=116^2\)

\(\Leftrightarrow2x+3\sqrt{x}-3=116\) hoặc \(2x+3\sqrt{x}-3=-116\)

\(\Leftrightarrow2x+3\sqrt{x}-119=0\) hoặc \(2x+3\sqrt{x}+113=0\)

Với \(2x+3\sqrt{x}-119=0\)

\(\Leftrightarrow\left(\sqrt{x}-7\right)\cdot\left(2\sqrt{x}+17\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=7\\\sqrt{x}=-\dfrac{17}{2}\left(vô.lý\right)\end{matrix}\right.\)

\(\Leftrightarrow x=49\)

Với \(2x+3\sqrt{x}+113=0\)

\(\Leftrightarrow PTVN\) (Phương trình vô nghiệm).

\(\Rightarrow\) Vậy \(S=\left\{49\right\}\)

a; \(x^2\) - 5\(x\) + m = 0

  Với m  = 6 ta có:

     \(x^2\) - 5\(x\) + 6 = 0

   \(\Delta\) =  (-5)² - 4.1.6 = 1 > 0

Vậy  phương trình có hai nghiệm phân biệt lần lượt là:

    \(x_1\) = \(\dfrac{-\left(-5\right)+\sqrt{1}}{2.1}\) = 3

   \(x_2\) = \(\dfrac{-\left(-5\right)-\sqrt{1}}{2.1}\) = 2

b; \(x^2\) - 5\(x\) + m = 0

    △ = (-5)² - 4.m.1 = 25 - 4m

    Để phương trình có hai nghiệm phân biệt thì △ > 0

    ⇒ 25 - 4m > 0  ⇒ m < \(\dfrac{25}{4}\)

  Với m < \(\dfrac{25}{4}\) thì phương trình có hai nghiệm phân biệt \(x_1\) và \(x_2\)

   Áp dụng vi-et ta có:

     \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1.x_2=m\end{matrix}\right.\) (1)

    Theo bài ra ta có:

   |\(x_1\) - \(x_2\)| = 3 ⇒ (\(x_1\) - \(x_2\))² = 9 ⇒ (\(x_1\) + \(x_2\))² - 4\(x_1\).\(x_2\) = 9  (2)

Thay (1) vào (2) ta có:

5² - 4m = 9 ⇒ 4m = 25 - 9 ⇒ 4m = 16 ⇒m = 4 < \(\dfrac{25}{4}\) (nhận)

Vậy với m = 4 thì phương trình có hai nghiệm phân biệt thỏa mãn

  |\(x_1\) - \(x_2\)| = 3

a) với m=0 ta có pt :

x² + 3x - 4 = 0 

Δ = 3² - 4. (-4)  = 25 > 0 => pt có 2 nghiệm phân biệt

\(\sqrt{\Delta}=5\)

x₁ = \(\dfrac{-3+5}{2}=1\)

x₂ = \(\dfrac{-3-5}{2}=-4\)

vậy với m=0 thì S= { -4;1 }

b) để pt có 2 nghiệm thì Δ > 0

=>  3² - 4.( -m - 4 ) > 0

<=>  25 + 4m > 0 

<=> m > \(-\dfrac{25}{4}\)

khi đó theo viet có : \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1.x_2=-m-4\end{matrix}\right.\)       (*)

theo bài ta ta có : x₁ = 2x₂  => x₁ - 2x₂ = 0  

có hệ pt : \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1-2x_2=0\end{matrix}\right.\)      <=> 3x₂ = -3    <=>  x₂ = -1

=>  x1 = -2

thay x1 = -2  , x2 = -1  vào (*) :

-2 . (-1) = -m - 4

<=> -m - 4 = 2

<=>  -m = 6

<=>  m = -6 ( thỏa mãn )

vậy m = -6

a/

Ta có M và A cùng nhìn OC dưới 1 góc \(90^o\) => ACMO là tứ giác nội tiếp

b/

Xét tg vuông BED và tg vuông AEC có \(\widehat{BED}\) chung

=> tg BED đồng dạng với tg AEC (g.g.g)

\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DE}{CE}\)

Mà 

\(DB=DM;CA=CM\) (Hai tiếp tuyến cùng xp từ 1 điểm...)\(\Rightarrow\dfrac{DB}{CA}=\dfrac{DM}{CM}=\dfrac{DE}{CE}\Rightarrow DM.CE=CM.DE\)

c/

Ta có

\(CA\perp AB\left(gt\right);DB\perp AB\left(gt\right)\) => CA//DB

\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DB}{CA}\) (Talet)

Mà \(\dfrac{DM}{CM}=\dfrac{DB}{CA}\left(cmt\right)\)

\(\Rightarrow\dfrac{BN}{CN}=\dfrac{DM}{CM}\) => MN//BD (Talet đảo trong tam giác)

a/

Xét \(\Delta ABC\)

AD và BE cắt nhau tại H (gt) 

\(\Rightarrow CH\perp AB\) (trong tam giác 3 đường cao đồng quy)

b/ Gọ F là giao của CH với AB ta có

F và D cùng nhìn BH dưới 1 góc \(90^o\) => F và H nằm trên đường tròn đường kính BH => Tứ giác BFHD là tứ giác nội tiếp)

Ta có

\(sđ\widehat{ABC}=\dfrac{1}{2}sđcungFHD\) (góc nt đường tròn)

\(sđ\widehat{FHD}=\dfrac{1}{2}sđcungFBD\) (góc nt đường tròn)

\(\Rightarrow sđ\widehat{ABC}+sđ\widehat{FHD}=\dfrac{1}{2}\left(sđcungFHD+sđcungFBD\right)\)

Mà \(sđcungFHD+sđcungFBD=360^o\)

\(\Rightarrow sđ\widehat{ABC}+sđ\widehat{FHD}=\dfrac{1}{2}.360^o=180^o\)

Mà \(\widehat{CHI}+\widehat{FHD}=\widehat{FHC}=180^o\)

\(\Rightarrow\widehat{CHI}=\widehat{ABC}\) (cùng bù với \(\widehat{FHD}\) ) (1)

Xét (O) có 

\(\widehat{ABC}=\widehat{AIC}\) (góc nt đường tròn cùng chắn cung AC) (2)

Từ (1) và (2) \(\Rightarrow\widehat{CHI}=\widehat{AIC}\) => tg CHI cân tại C

c/

Chứng minh tương tự ta cũng có CHK là tg cân tại C

Ta có

\(BE\perp AC\left(gt\right)\Rightarrow AC\perp HK\)

\(\Rightarrow EH=EK\) (trong tg cân đường cao xp từ đỉnh tg cân đồng thời là đường trung tuyến)

=> H đối xứng K qua AC

d/ Gọi G là giao của CO với (O)

Ta có tg CHK cân tại C (cmt)

=> CK=CH

Mà tg CHI cân tại C (cmt) => CH=CI

=> CK=CI => tg CKI cân tại C (3)

Ta có

\(sđ\widehat{CKI}=\dfrac{1}{2}sđcungCI\) (góc nt (O))

\(sđ\widehat{CIK}=\dfrac{1}{2}sđcungCK\) (góc nt (O))

\(\Rightarrow sđcungCI=sđcungCK\)

Ta có 

sđ cung CIG = sđ cung CKG \(=180^o\)

=> sđ cung CIG - sđ cung CI = sđ cung CKG - sđ cung CK

=> sđ cung GBI = sđ cung GAK

Ta có

\(sđ\widehat{ICG}=\dfrac{1}{2}sđcungGBI\) (góc nt (O))

\(sđ\widehat{KCG}=\dfrac{1}{2}sđcungGAK\) (góc nt (O))

\(\Rightarrow\widehat{ICG}=\widehat{KCG}\) => CG là phân giác của \(\widehat{KCI}\) (4)

Từ (3) và (4) => \(OC\perp KI\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao)

e/

Ta có E và D cùng nhìn CH dưới 1 góc \(90^o\) => CDHE là tứ giác nội tiếp

\(\Rightarrow\widehat{HDE}=\widehat{ECF}\) (góc nt cùng chắn cung HE) (5)

Ta có F và E cùng nhìn BC dưới 1 góc \(90^o\) => BCEF là tứ giác nt

\(\Rightarrow\widehat{ABK}=\widehat{ECF}\) (góc nt cùng chắn cung EF) (6)

Xét (O) có

\(\widehat{ABK}=\widehat{AIK}\) (góc nt cùng chắn cung AK) (7)

Từ (5) (6) (7) \(\Rightarrow\widehat{HDE}=\widehat{AIK}\) mà 2 góc này ở vị trí đồng vị nên

=> ED//KI 

Mà \(OC\perp KI\left(cmt\right)\)

\(\Rightarrow OC\perp ED\)

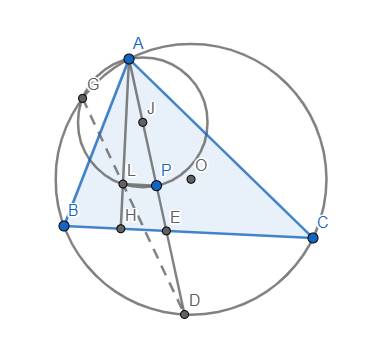
a) Gọi J là tâm đường tròn (AP)

 Xét đường tròn (J) có đường kính AP, \(L\in\left(J\right)\) nên \(\widehat{ALP}=90^o\) hay \(AH\perp LP\) tại L.

 Lại có \(AH\perp BC\) nên LP // BC.

 \(\Rightarrow\widehat{DPL}=\widehat{DEB}\) 

 Mặt khác, \(\widehat{DEB}=\dfrac{sđ\stackrel\frown{AC}+sđ\stackrel\frown{BD}}{2}\) \(=\dfrac{sđ\stackrel\frown{AC}+sđ\stackrel\frown{CD}}{2}\) \(=\dfrac{sđ\widehat{AD}}{2}\) \(=\widehat{AGD}\)

 Tứ giác AGLP nội tiếp nên \(\widehat{DPL}=\widehat{AGL}\)

 Từ đó suy ra \(\widehat{AGD}=\widehat{AGL}\)

 Hơn nữa, L, D nằm cùng phia đối với đường thẳng GA nên suy ra G, L, D thẳng hàng (đpcm).

Gọi số học sinh lớp 9B là : \(x\) (học sinh) \(\left(x\inℕ^∗\right)\)

\(\Rightarrow\) Số học sinh lớp 9A là : \(x+10\) (học sinh)

Số cây học sinh lớp 9B trồng được : \(4x\) (cây)

Số cây học sinh lớp 9A trồng được : \(3\left(x+10\right)\) (cây)

Vì tổng số cây 2 lớp trồng được là : 275 cây

Nên ta có pt :

\(3\left(x+10\right)+4x=275\\ \Rightarrow3x+30+4x=275\\ \Rightarrow7x=245\\ \Rightarrow x=35\left(TMDK\right)\)

Vậy số HS lớp 9B là : 35 HS và lớp 9A là : 35+10=45(HS)

HS lớp 9B là 35hs. HS lớp 9A là 45hs.