Cho dãy số (\(u_n\)) xác định: \(\left\{{}\begin{matrix}u_1=5\\u_{n+1}=2u_n-3\end{matrix}\right.\).Tìm giới hạn lim(\(\dfrac{u_n}{2^n}\))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


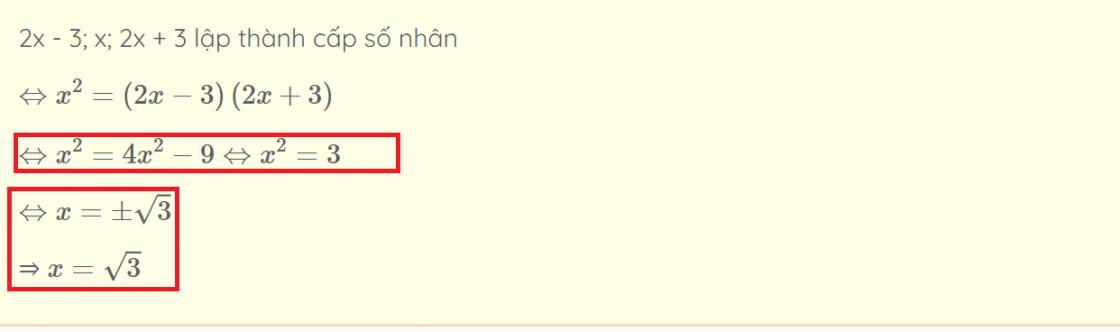
`x^2 = 4x^2 - 9`
`<=> 9 = 4x^2 - x^2`
`<=> 9 = 3x^2`
`<=> x^2 = 3.`
`<=> x = +-sqrt 3`.

$(u_n)$ là cấp số cộng với công sai d nên:
$u_{3n+1}=u_{3n}+d=u_{3n-1}+d+d=u_{3n-2}+d+d+d=u_{3(n-1)+1}+3d$
Do đó: $(u_{3n+1})$ với $n=0,1,2,...$ là cấp số cộng có công sai $3d$
Đặt $3d=d'$ thì ta có như lời giải.


Ta chứng minh bằng quy nạp:
- Với \(n=4\) BĐT trở thành \(3^3>4.6\) (đúng)
- Giả sử BĐT đúng với \(n=k\ge4\) hay \(3^{k-1}>k\left(k+2\right)\)
Ta cần chứng minh BĐT cũng đúng với \(n=k+1\)
Hay \(3^k>\left(k+1\right)\left(k+3\right)\)
Thật vậy, ta có:
\(3^k=3.3^{k-1}>3.k\left(k+2\right)=\left(k+1\right)\left(k+3\right)+2k^2+2k-3\)
Do \(k\ge4\Rightarrow k-3>0\Rightarrow2k^2+2k-3>0\)
\(\Rightarrow\left(k+1\right)\left(k+3\right)+2k^2+2k-3>\left(k+1\right)\left(k+3\right)\)
\(\Rightarrow3^k>\left(k+1\right)\left(k+3\right)\) (đpcm)

Gọi số tự nhiên gồm 4 chữ số là: abcd
Trường hợp 1: d=0 (1 cách)
a : 6 cách ( #0); b: 5 cách; c:4 cách => 120 cách
TH2: d#0 ( nhận 2 4 6 => 1 cách)
a: 5 cách (#0; #d); b : 4 cách; c: 3 cách => 60 cách
=> TH1 + TH2 = 200 cách
ý lộn TH2: b: 5 cách(#a; #d); c: 4 cách => 100 cách
=> Tổng cộng 220 cách

b. Kéo dài AB và DE, cắt nhau tại P.
BE là đường trung bình của tam giác APD.
EF là đường trung bình tam giác DSP nằm trong mp (DSP)
tam giác SAB chính là mp (ASB) hay mp (ASP)
EF song song SP, tức song song ASP hay mp (ASB) hay là mp ( SAB)

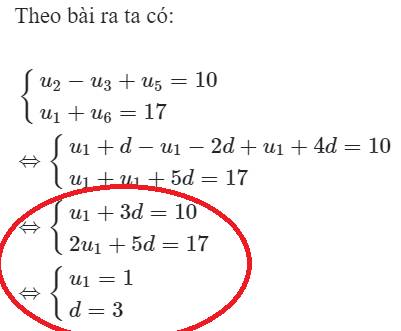

Là 6