Trong mặt phẳng tọa độ Oxy, xét đường thẳng (d): \(\text{y = mx + 4}\) với \(\text{m ≠ 0}\).
a. Gọi A là giao điểm của đường thẳng (d) và trục Oy. Tìm tọa độ của điểm A.
b. Tìm tất cả các giá trị của m để đường thẳng (d) cắt trục Ox tại điểm B sao cho tam giác OAB là tam giác cân.



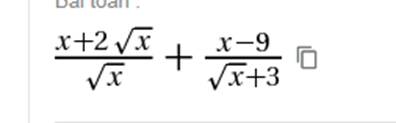
vì A là giao điểm của d và Oy nên A(0;y)
vì A \(\in\) d nên tọa độ A thỏa mãn :
y = m . 0 + 4 = 4
tọa độ của A là : A(0;4)
vì B cắt trục Ox tại B nên B(x;0)
vì B \(\in\) d nên tọa độ B thỏa mãn
0 = m.x + 4
x = \(\dfrac{-4}{m}\)
Để tam giác OAB cân tại O thì |\(\dfrac{-4}{m}\)| = 4
|m| = 1
m = 1 và m= -1
kết luận : A(0;4) và m = 1 và m = -1