a

lêu

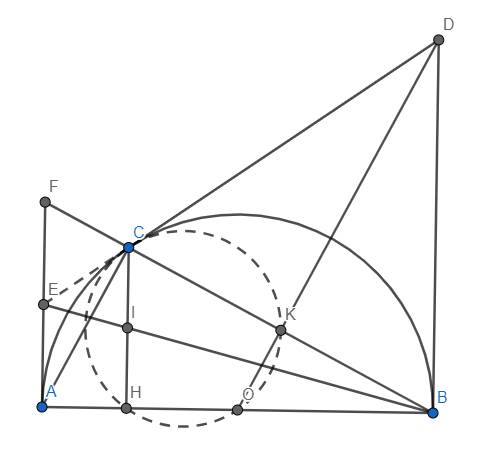
a) Ta thấy OK là đường trung bình của tam giác ABC \(\Rightarrow\) OK//AC.

Mà \(AC\perp CB\) tại C nên \(OK\perp BC\) tại K hay \(DK\perp BC\) tại K

 Tam giác BCD có DK vừa là đường cao, vừa là trung tuyến nên tam giác BCD cân tại D, suy ra \(DB=DC\) (đpcm)

 Dễ dàng chứng minh \(\Delta OBD=\Delta OCD\left(c.c.c\right)\) \(\Rightarrow\widehat{OCD}=\widehat{OBD}=90^o\), suy ra DC tiếp xúc với (O) tại C. (đpcm)

 b) Tứ giác OHCK có \(\widehat{CHO}+\widehat{CKO}=90^o+90^o=180^o\) nên OHCK nội tiếp, điều này có nghĩa là \(C\in\left(OHK\right)\) (đpcm)

 c) Gọi F là giao điểm của BC và AE. Do CH//AF nên theo bổ đề hình thang, E là trung điểm của AF.

 Tam giác CAF vuông tại C có trung tuyến CE nên \(CE=\dfrac{1}{2}AF=EA\), suy ra tam giác ACE cân tại E 

 \(\Rightarrow\widehat{ECA}=\widehat{EAC}\)

Mặt khác, EA tiếp xúc với (O) tại A nên \(\widehat{EAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\)

Từ đó suy ra \(\widehat{EAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) \(\Rightarrow\) EC tiếp xúc với (O) tại C.

Mà DC cũng tiếp xúc với (O) tại C nên D, E, C thẳng hàng (đpcm)

Bài 4:

Ta có \(\dfrac{1}{a^2\left(b+c\right)}=\dfrac{abc}{a^2\left(b+c\right)}=\dfrac{bc}{ab+ca}\)

Tương tự: \(\dfrac{1}{b^2\left(c+a\right)}=\dfrac{ca}{bc+ab}\) và \(\dfrac{1}{c^2\left(a+b\right)}=\dfrac{ab}{bc+ca}\)

Đặt \(\left\{{}\begin{matrix}bc=x\\ca=y\\ab=z\end{matrix}\right.\) với \(x,y,z>0;xyz=1\)

Khi đó BĐT cần chứng minh trở thành:

 \(\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\ge\dfrac{3}{2}\) 

Thật vậy, đặt \(P=\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\)

\(P=\dfrac{x^2}{xy+zx}+\dfrac{y^2}{yz+xy}+\dfrac{z^2}{zx+yz}\)

\(P\ge\dfrac{\left(x+y+z\right)^2}{2\left(xy+yz+zx\right)}\) (BĐT B.C.S)

Mà lại có \(xy+yz+zx\le\dfrac{\left(x+y+z\right)^2}{3}\) nên ta có:

\(P\ge\dfrac{\left(x+y+z\right)^2}{2.\dfrac{\left(x+y+z\right)^2}{3}}=\dfrac{3}{2}\) Vậy ta có đpcm. 

Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\) \(\Leftrightarrow a=b=c=1\)

P1: AA  x AA => F1(P1): 100% AA (Mắt đen 100%)

P2: AA x Aa => F1(P2): 1AA: 1Aa (Mắt đen 100%)

P3: AA x aa => F1(P3): 100% Aa (Mắt đen 100%)

P4: Aa x Aa => F1(P4): 1AA:2Aa:1aa (3 Mắt đen: 1 mắt nâu)

P5: AA x aa : Như P3

P6: aa x aa => F1(P6): 100% aa (Mắt nâu 100%)

Để hát quốc ca đúng như quy định, học sinh phải thực hiện các yêu cầu sau: Tư thế khi hát quốc ca phải nghiêm trang, đứng thẳng, mắt nhìn thẳng vào hướng lá cờ tổ quốc. Phải giữ trật tự trước và sau khi hát quốc ca. Khi hát phải theo hiệu lệnh để việc đồng ca diễn ra đồng đều.

cụ nhất kokushibo cop mạng

ồ ,em mới lớp 8 mà đã học rồi ạ!Em chỉ nêu ý cần viết thôi ạ!Cj có thể thêm "Ôi, quả một vị vua vĩ đại;một vị chủ tướng tài ba,tâm lí,biết yên ủi,động viên và khích lệ quân lính để thắp cháy nên ngọn lửa yêu nước,thù giặc đầy nhiệt huyết của họ"cho thành phần cảm thản.

   Lời phủ dụ của vua Quang Trung

-Khẳng định chủ quyền dân tộc

-Lên án,chỉ trích hành động xâm lược phi nghĩa của giặc;trái với đạo trời

-Tự hào về những công lao,chiến công,chiến tích chống giặc ngoại xâm của các thế hệ đi trước

-Tin tưởng vào cuộc hành binh của đạo quân và kêu gọi binh sõ tham gia

-Ra kỉ luật với các chiến sĩ

           ---------------------------HẾT-------------------------------

Trả lời bằng Tiếng Anh hay bằng Tiêng Việt?

Không trả lời được thì đừng có bl ạ? 

Ta có \(\sqrt{x+2}-y^3=\sqrt{y+2}-x^3\)

\(\Leftrightarrow\sqrt{x+2}+x^3=\sqrt{y+2}+y^3\)

 Đặt \(f\left(x\right)=\sqrt{x+2}+x^3\). Ta chứng minh \(f\left(x\right)\) là hàm số đồng biến với \(x\ge-2\)

Giả sử \(f\left(a\right)>f\left(b\right)\) với \(a,b\ge-2\)

\(\Rightarrow\sqrt{a+2}+a^3>\sqrt{b+2}+b^3\)

\(\Leftrightarrow\sqrt{a+2}-\sqrt{b+2}+a^3-b^3>0\)

\(\Leftrightarrow\dfrac{a-b}{\sqrt{a+2}+\sqrt{b+2}}+\left(a-b\right)\left(a^2+ab+b^2\right)>0\)

\(\Leftrightarrow\left(a-b\right)\left(\dfrac{1}{\sqrt{a+2}+\sqrt{b+2}}+a^2-ab+b^2\right)>0\)     (*)

 Dễ thấy \(\dfrac{1}{\sqrt{a+2}+\sqrt{b+2}}+a^2+ab+b^2>0\) với mọi \(a,b\ge-2\)

 Do đó từ (*) suy ra \(a>b\).

 Vậy ta có \(f\left(a\right)>f\left(b\right)\Rightarrow a>b\). Do đó \(f\) là hàm số đồng biến.

 Theo trên, ta có \(f\left(x\right)=f\left(y\right)\Rightarrow x=y\)

 Thay vào biểu thức B, ta có \(B=x^2+2x+10\)

\(B=\left(x+1\right)^2+9\) \(\ge9\).

 Dấu "=" xảy ra \(\Leftrightarrow x=-1\) (nhận) \(\Rightarrow y=-1\)

 Vậy GTNN của B là 9, xảy ra khi \(\left(x;y\right)=\left(-1;-1\right)\)