Giá trị của biểu thức : Cho : 1/a^150 < (1/5)^225 . Giá trị nguyên dương a nhỏ nhất thoả mãn là :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.\dfrac{3}{7}=\dfrac{2x+1}{3x+5}\\ 3\left(3x+5\right)=7\left(2x+1\right)\\ 9x+15=14x+7\\ 14x-9x=15-7\\ 5x=8\\ x=\dfrac{8}{5}\\ b.\dfrac{x+1}{x-2}=\dfrac{3}{4}\\ 3\left(x-2\right)=4\left(x+1\right)\\ 3x-6=4x+4\\ 4x-3x=-6-4\\ x=-10\\ c.\dfrac{2x+3}{7}=\dfrac{4x-1}{15}\\ 15\left(2x+3\right)=7\left(4x+1\right)\\ 30x+45=28x+7\\ 30x-28x=7-45\\ 2x=-38\\ x=\dfrac{-38}{2}=-19\\ d.\dfrac{6x-5}{-7}=\dfrac{5x-3}{-5}\\ -5\left(6x-5\right)=-7\left(5x-3\right)\\ -30x+25=-35x+21\\ -30x+35x=21-25\\ 5x=-4\\ x=-\dfrac{4}{5}\)

a) ABCD là hình thang
=> \(\widehat{A}+\widehat{D}=180^o=>\widehat{A}=180^o-\widehat{D}\)
Mà:
\(\widehat{A}-\widehat{D}=20^o=>180^o-\widehat{D}-\widehat{D}=20^o\\ =>2\widehat{D}=180^o-20^o=160^o\\ =>\widehat{D}=\dfrac{160^o}{2}=80^o\)
=> \(\widehat{A}=180^o-80^o=100^o\)
\(\widehat{B}+\widehat{C}=180^o\) (ABCD là hình thang)
Mà: \(\widehat{B}=2\widehat{C}=>2\widehat{C}+\widehat{C}=180^o=>3\widehat{C}=180^o=>\widehat{C}=60^o\)
\(=>\widehat{B}=2\cdot60^o=120^o\)
b) Xét ΔABC có: \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(=>\widehat{BAC}=180^o-120^o-50^o=10^o\)
Mà: \(\widehat{DAC}+\widehat{BAC}=\widehat{DAB} =>\widehat{DAC}=\widehat{DAB}-\widehat{BAC}=100^o-10^o=90^o\)
`=> AD⊥AC`

\(\dfrac{3x+2}{3}=\dfrac{-4}{5}\\ =>5\left(3x+2\right)=-4\cdot3\\ =>5\left(3x+2\right)=-12\\ =>3x+2=-\dfrac{12}{5}\\ =>3x=-\dfrac{12}{5}-2\\ =>3x=-\dfrac{22}{5}\\ =>x=\dfrac{-22}{5}:3\\ =>x=\dfrac{-22}{15}\)

Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k=>\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
a) \(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{dk}{dk+d}=\dfrac{c}{c+d}\)
b) \(\dfrac{2a+5b}{3a-4b}=\dfrac{2bk+5b}{3bk-4b}=\dfrac{b\left(2k+5\right)}{b\left(3k-4\right)}=\dfrac{2k+5}{3k-4}=\dfrac{d\left(2k+5\right)}{d\left(3k-4\right)}=\dfrac{2dk+5d}{3dk-4d}=\dfrac{2c+5d}{3c-4d}\)
c) \(\dfrac{2018a-2019b}{2019c+2020d}=\dfrac{2018bk-2019b}{2019dk+2020d}=\dfrac{b\left(2018k-2019\right)}{d\left(2019k+2020\right)}=\dfrac{b}{d}\cdot\dfrac{2018k-2019}{2019k+2020}\) (1)
Mà: \(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{b}{d}=\dfrac{c}{a}\)
\(\left(1\right)=\dfrac{c}{a}\cdot\dfrac{2018k-2019}{2019k+2020}=\dfrac{2018ck-2019c}{2019ak+2020a}=\dfrac{2018ck-2019dk}{2019ak+2020bk}\\ =\dfrac{k\left(2018c-2019d\right)}{k\left(2019a+2020b\right)}=\dfrac{2018c-2019d}{2019a+2020b}\)

(5.3^5) + 17.3^4) : 6^2
= (5.243 + 17.81) : 36
= (1215 + 1377) : 36
= 2592 : 36
= 72

a) Trong mặt phẳng (SAC), gọi I là giao điểm của AO và MN. Khi đó vì \(MN\subset\left(BMN\right)\) nên I chính là giao điểm của (BMN) và SO.
b) Ta có \(I\in SO\subset\left(SBD\right)\) nên \(I\in\left(SBD\right)\). Trong mặt phẳng (SBD), gọi K là giao điểm của BI và SD. Khi đó vì \(K\in BI\subset\left(BMN\right)\) nên K chính là giao điểm của (BMN) và SD.
a: Trong mp(SAC), gọi K là giao điểm của MN với SO
mà MN\(\in\left(BMN\right)\)
nên \(K=SO\cap\left(BMN\right)\)
b: Vì K là giao của MN và SO
mà \(MN\in\left(BMN\right);SO\in\left(SBD\right)\)
nên \(K\in\left(BMN\right)\cap\left(SBD\right)\)
mà \(B\in\left(BMN\right)\cap\left(SBD\right)\)
nên \(\left(BMN\right)\cap\left(SBD\right)=BK\)
Gọi E là giao điểm của BK với SD
=>K là giao điểm của SD với (BMN)

Gọi các số nguyên tố liên tiếp tăng dần là \(p_1,p_2,p_3,...\) với \(p_1=2,p_2=3,p_3=5,...\)
Giả sử tồn tại \(m>1\) để với mọi \(n\inℕ^∗\) thì \(p_{n+1}-p_n\le m\) hay \(p_n\ge p_{n+1}-m\)
Khi đó, với mọi \(n\inℕ^∗\) thì:
\(p_1\ge p_2-m\ge p_3-2m\ge...\ge p_{n+1}-nm\)
Suy ra \(p_{n+1}\ge mn+2\) hay \(m\le\dfrac{p_{n+1}-2}{n}\) với mọi \(n\inℕ^∗\). Tuy nhiên, nếu cho \(n=1\) thì \(m\le\dfrac{p_2-2}{1}=1\), vô lý vì \(m>1\).
Vậy điều giả sử là sai \(\Rightarrow\) đpcm.
ý tưởng chứng minh bằng phản chứng của anh Lê Song Phương rất hay. Tuy nhiên, đề bài cần chứng minh là:
\(\forall m>1,m\inℕ,\exists n\inℕ\) sao cho \(p_{n+1}-p_n>m\)
Nếu nhìn kỹ hơn thì đề bài có thể mở rộng thêm 1 chút
\(\forall m\inℕ,\exists n\inℕ\) sao cho \(p_{n+1}-p_n>m\)

a)
\(2\sqrt{x}< 16\\ \Leftrightarrow\sqrt{x}< 8\\ \Leftrightarrow x< 64\)
Vậy...
b)
\(3\sqrt{x}+2=0\\ \Leftrightarrow3\sqrt{x}=-2\\ \Leftrightarrow\sqrt{x}=-\dfrac{2}{3}\)
Nhận xét:
\(\sqrt{x}\) xác định khi và chỉ khi \(\sqrt{x}>0\)
Mà \(-\dfrac{2}{3}< 0\) nên:
Không có giá trị x thoả mãn
Vậy...
c)
\(\sqrt{1-2x^2}=x-1\)
Nhận xét:
\(\sqrt{1-2x^2}\) xác định khi và chỉ khi \(\sqrt{1-2x^2}>0\)
Suy ra:
\(x-1>0\)
\(\Leftrightarrow x>1\)
\(\Leftrightarrow1-2x^2< 0\) (vô lí)
Vậy...
d)
\(2\sqrt{x}-6>0\\ \Leftrightarrow2\sqrt{x}>6\\ \Leftrightarrow\sqrt{x}>3\\ \Leftrightarrow x>9\)
Vậy...

1) 15.9^3 : 27 - 6^2.12 +18.41
= 15.729 : 27 - 36.12 +738
= 10935 : 27 - 432 + 738
= 405 - 432 + 738
= 711
2) 18.7^3 + 9.2^6 :8 - 12.7
= 18.343 + 9.64 :8 - 84
= 6174 + 72 - 84
= 6162
3) 23.2^5 + 288.4^2 :12
= 23.32 + 288.16 :12
= 736 + 384
= 1120
4) 12^2 : 36 + 8^2 : 4 - 5.3
= 144 : 36 + 64 : 4 - 15
= 4 + 16 - 15
= 5

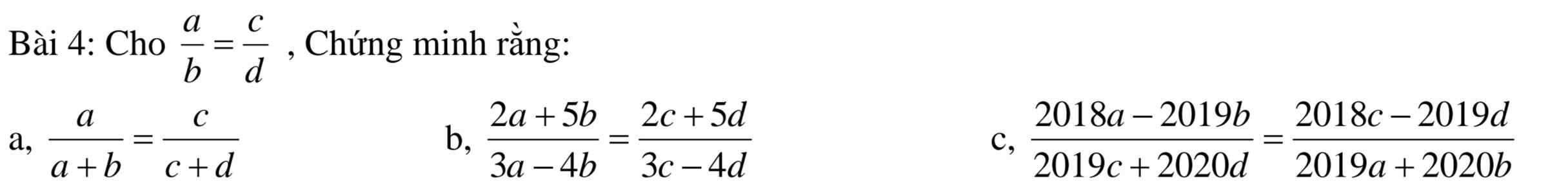
Ta có:
a² > 125
a = 12 (vì a là số nhỏ nhất)