tìm số tự nhiên x,y biết : 3-y=2(x-1)^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để A là phân số thì \(n+1\ne0\)
=>\(n\ne-1\)
b: Để A là số nguyên thì \(4n+2⋮n+1\)
=>\(4n+4-2⋮n+1\)
=>\(-2⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2\right\}\)
=>\(n\in\left\{0;-2;1;-3\right\}\)
c: \(A=\dfrac{4n+2}{n+1}=\dfrac{4n+4-2}{n+1}=4-\dfrac{2}{n+1}\)
Để A nhỏ nhất thì \(-\dfrac{2}{n+1}\) nhỏ nhất
=>n+1=1
=>n=0

c: Số điểm tất cả là 4+2018+1=2023(điểm)
Số đoạn thẳng có hai đầu mút là hai điểm trong số các điểm đã cho là:
\(\dfrac{2023\cdot2022}{2}=2045253\left(đoạn\right)\)

Số giao điểm của 105 đường còn lại với nhau là \(C^2_{105}=5460\left(giao\right)\)
Số giao điểm của 105 đường còn lại với 5 đường đã cho là
\(105\cdot5=525\left(giao\right)\)
Tổng số giao điểm là:
5460+525+1=5986(giao)

Giải:
a; Số học sinh giỏi là: 42 x \(\dfrac{1}{7}\) = 6 (học sinh)
Số học sinh trung bình là: 42 x \(\dfrac{2}{3}\) = 28 (học sinh)
Số học sinh khá là: 42 - 6 - 28 = 8 (học sinh)
b; Tỉ số phần trăm số học sinh giỏi và số học sinh của cả lớp là:
6 : 42 x 100% = 14,29%
Kết luận: a; học sinh giỏi 6 học sinh
học sinh khá 8 học sinh
học sinh trung bình 28 học sinh
b; học sinh giỏi chiếm số phần trăm là 14,29%
a: Số học sinh giỏi là \(42\cdot\dfrac{1}{7}=6\left(bạn\right)\)
Số học sinh còn lại là 42-6=36(bạn)
Số học sinh trung bình là \(36\cdot\dfrac{2}{3}=24\left(bạn\right)\)
Số học sinh khá là 36-24=12(bạn)
b: Số học sinh giỏi chiếm:
\(\dfrac{1}{7}\simeq14,29\%\)(lớp)

y.(\(2x+3\)) = 9 - 2\(x\) (\(x;y\in Z\))
y = (9 - 2\(x\)) : (\(2x+3\))
y \(\in\) Z ⇔ 9 - 2\(x\) ⋮ 2\(x\) + 3
-(2\(x\) + 3) + 12 ⋮ 2\(x\) + 3
12 ⋮ 2\(x\) + 3
2\(x\) + 3 \(\in\) Ư(12) = {-12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
Lập bảng ta có:
| 2\(x\) + 3 | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | 12 |
| \(x\) | -15/2 | -9/2 | -7/2 | -3 | -5/2 | -2 | -1 | -1/2 | 0 | 1/2 | 3/2 |
11/2 |
| y = \(\dfrac{9-2x}{2x+3}\) | -5 | -13 | 11 | 3 | ||||||||
| Loại | loại | loại | loại | loại | loại | loại |
Vậy các cặp \(x\); y nguyên thỏa mãn đề bài là:
(\(x;y\)) = (-3; -5); (-2; -13); (0; 3)
y(2x+3)=9-2x
=>\(y\left(2x+3\right)+2x-9=0\)
=>\(y\left(2x+3\right)+2x+3-12=0\)
=>\(\left(2x+3\right)\left(y+1\right)=12\)
=>\(\left(2x+3\right)\left(y+1\right)=1\cdot12=12\cdot1=\left(-1\right)\cdot\left(-12\right)=\left(-12\right)\cdot\left(-1\right)=3\cdot4=4\cdot3=\left(-3\right)\cdot\left(-4\right)=\left(-4\right)\cdot\left(-3\right)=2\cdot6=6\cdot2=\left(-2\right)\cdot\left(-6\right)=\left(-6\right)\cdot\left(-2\right)\)
=>\(\left(2x+3;y+1\right)\in\){(1;12);(12;1);(-1;-12);(-12;-1);(2;6);(6;2);(-2;-6);(-6;-2);(3;4);(4;3);(-3;-4);(-4;-3)}
=>(x;y)\(\in\){(-1;11);(9/2;0);(-2;-13);(-15/2;-2);(-1/2;5);(3/2;1);(-5/2;-7);(-9/2;-3);(0;3);(1/2;2);(-3;-5);(-7/2;-4)}


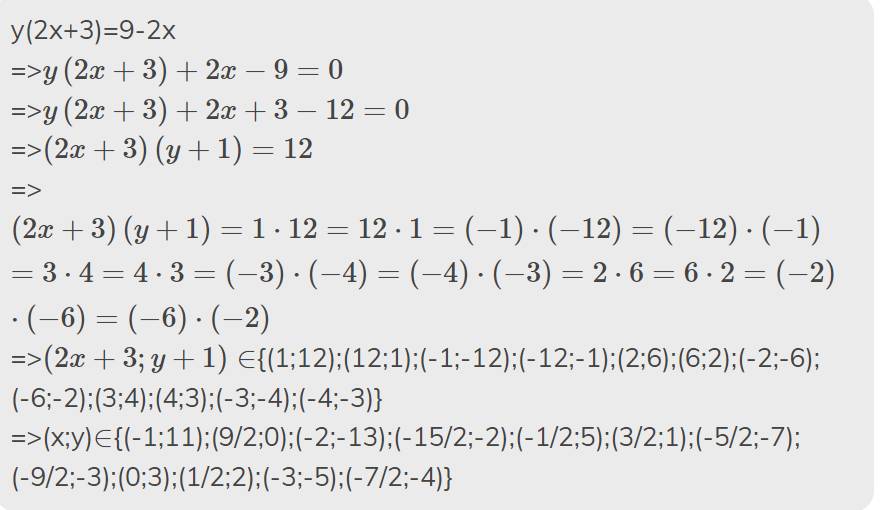
Ta có: \(3-y=2\left(x-1\right)^2\) (*) và \(2\left(x-1\right)^2\ge0\forall x\)
nên \(3-y\ge0\Rightarrow y\le3\)
\(\Rightarrow y\in\left\{0;1;2;3\right\}\) (vì y là số tự nhiên) (1)
Mặt khác: \(2\left(x-1\right)^2\) là số chẵn với mọi x tự nhiên
\(\Rightarrow3-y\) chẵn \(\Rightarrow y\) lẻ (2)
Từ (1) và (2) \(\Rightarrow y\in\left\{1;3\right\}\)
+, Với \(y=1\) thì (*) thành: \(3-1=2\left(x-1\right)^2\)
\(\Rightarrow2\left(x-1\right)^2=2\)
\(\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(tm\right)\end{matrix}\right.\)
+, Với \(y=3\) thì (*) thành: \(3-3=2\left(x-1\right)^2\)
\(\Rightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Rightarrow x=1\left(tm\right)\)
Vậy \(\left(x;y\right)\in\left\{\left(1;3\right);\left(2;1\right);\left(0;1\right)\right\}\) là các cặp giá trị cần tìm.
\(3-y=2\left(x-1^2\right)\)
\(=>\left(3-y\right)-2\left(x-1\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}3-y=0\\2\left(x-1\right)^2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=3\\\left(x-1\right)^2=0\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}y=3\\x-1=0\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}y=3\\x=1\end{matrix}\right.\)
Vậy x = 1; y = 3.