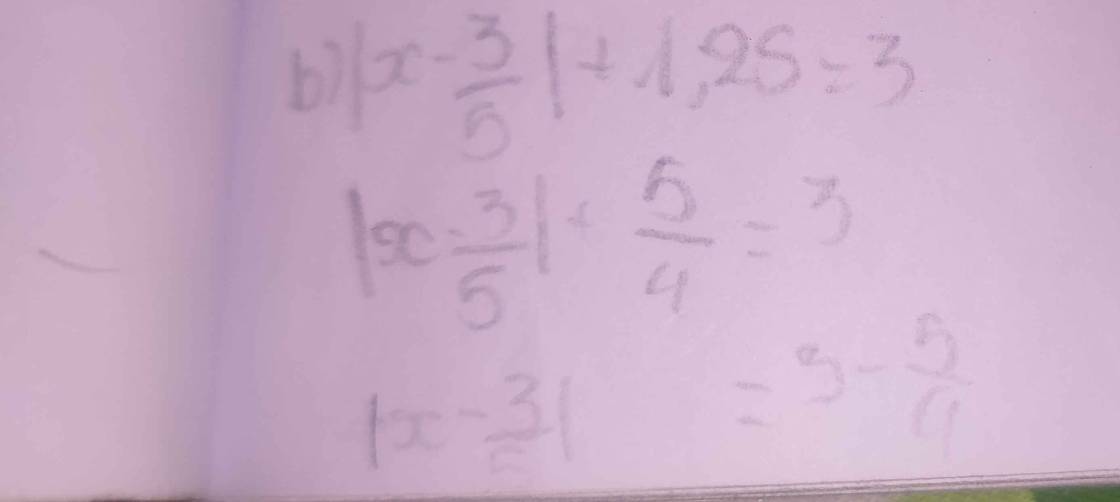hai thanh kim loại nhôm và sắt có thể tích bằng nhau, khối lượng riêng của chúng lần lượt là 2,7 g/cm3 và 7,8 g/cm3. tính khối lượng mỗi thanh kim loại. biết rằng tổng khối lượng của chúng là 1050g
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Giả sử chia 315 thành 3 phần có giá trị là $a,b,c$ tỉ lệ nghịch với $3,5,6$. Theo bài ra ta có:
$a+b+c=315$
$3a=5b=6c=\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{6}}$
Áp dụng TCDTSBN:
$3a=5b=6c=\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{6}}=\frac{a+b+c}{\frac{1}{3}+\frac{1}{5}+\frac{1}{6}}=\frac{315}{\frac{7}{10}}=450$
$\Rightarrow a=450:3=150; b=450:5=90; c=450:6=90$

Để x + 2y và 2x - y là số hữu tỷ, ta có thể thiết lập hệ phương trình sau:
x + 2y = a/b (1)
2x - y = c/d (2)
Trong đó a, b, c, d là các số nguyên và b, d khác 0.
Từ phương trình (1), ta có x = a/b - 2y. Thay vào phương trình (2), ta có:
2(a/b - 2y) - y = c/d
2a/b - 4y - y = c/d
2a/b - 5y = c/d
Để 2a/b - 5y là số hữu tỷ, ta cần 5y cũng là số hữu tỷ. Vì vậy, y phải là số hữu tỷ.
Tiếp theo, để x = a/b - 2y là số hữu tỷ, ta cần a/b - 2y cũng là số hữu tỷ. Vì y là số hữu tỷ, nên a/b - 2y cũng là số hữu tỷ.
Vậy, nếu x + 2y và 2x - y là số hữu tỷ, thì x và y đều là số hữu tỉ.

Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận với nhau nên đặt $y=kx$ với $k$ là hệ số tỉ lệ của $y$ so với $x$.
Thay $x=5; y=-15$ thì:
$-15=k.5\Rightarrow x=-3$
$\Rightarrow y=kx=-3x$
Khi $x=3$ thì $y=-3x=-3.3=-9$
Lời giải:
Vì $x,y$ là 2 đại lượng tỉ lệ thuận với nhau nên đặt $y=kx$ với $k$ là hệ số tỉ lệ của $y$ so với $x$.
Thay $x=5; y=-15$ thì:
$-15=k.5\Rightarrow x=-3$
$\Rightarrow y=kx=-3x$
Khi $x=3$ thì $y=-3x=-3.3=-9$

\(\left|x-\dfrac{1}{2}\right|-1=\dfrac{5}{2}\)
\(\Rightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{5}{2}+1\)
\(\Rightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{7}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{7}{2}\\x-\dfrac{1}{2}=-\dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)

(3x-2)2 = 2.23
<=> (3x-2)2 = 24
<=> (3x-2)2 = (22)2
<=> 3x-2 = 22 hoặc 3x-2 = -22
<=> 3x-2 = 4 hoặc 3x-2 = -4
<=> 3x = 6 hoặc 3x = -2
<=> x = 2 hoặc x = -2/3