Giup minh may cau duoc khoanh voi
minh cam on a!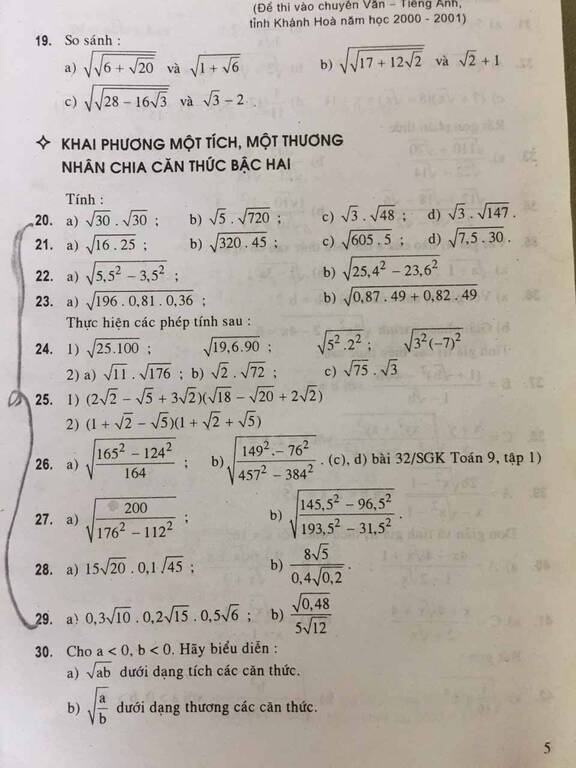 cau nay vs
cau nay vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
ĐKXĐ: \(x\ge\dfrac{1}{4}\)
PT \(\Leftrightarrow\sqrt{4x^2+2x+2}-\sqrt{4x-1}+2x^2+3x-3=0\)
\(\Leftrightarrow\left(\sqrt{4x^2+2x+2}-2\right)-\left(\sqrt{4x-1}-1\right)+2x^2+3x-2=0\)
\(\Leftrightarrow\dfrac{4x^2+2x+2-4}{\sqrt{4x^2+2x+2}+2}-\dfrac{4x-1-1}{\sqrt{4x-1}+1}+\left(2x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\dfrac{4x^2+2x-2}{\sqrt{4x^2+2x+2}+2}-\dfrac{4x-2}{\sqrt{4x-1}+1}+\left(2x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\dfrac{2\left(2x-1\right)\left(x+1\right)}{\sqrt{4x^2+2x+2}+2}-\dfrac{2\left(2x-1\right)}{\sqrt{4x-1}+1}+\left(2x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(\dfrac{2x+2}{\sqrt{4x^2+2x+2}+2}-\dfrac{2}{\sqrt{4x-1}+1}+x+2\right)=0\)
Mà \(\dfrac{2x+2}{\sqrt{4x^2+2x+2}+2}>0\)
\(\dfrac{2}{\sqrt{4x-1}+1}< 2\Leftrightarrow-\dfrac{2}{\sqrt{4x-1}+1}>-2\)
\(x+2>2\)
=> \(\dfrac{2x+2}{\sqrt{4x^2+2x+2}+2}-\dfrac{2}{\sqrt{4x-1}+1}+x+2>0\)
\(\Leftrightarrow2x-1=0\Leftrightarrow x=\dfrac{1}{2}\left(TM\right)\)
KL: Vậy PT có nghiệm \(S=\left\{\dfrac{1}{2}\right\}\)
2)
BĐT \(\Leftrightarrow\left[\dfrac{a^3}{b+2c}+\dfrac{b+2c}{9}.a\right]+\left[\dfrac{b^3}{c+2a}+\dfrac{c+2a}{9}.b\right]+\left[\dfrac{c^3}{a+2b}+\dfrac{a+2b}{9}.c\right]-\dfrac{1}{3}.\left(ab+bc+ca\right)\ge1\)
Áp dụng BĐT Cosi cho 2 số không âm:
\(\dfrac{a^3}{b+2c}+\dfrac{b+2c}{9}.a\ge2.\sqrt{\dfrac{a^3}{b+2c}.\dfrac{b+2c}{9}.a}=\dfrac{2a^2}{3}\)
Tương tự \(\Rightarrow\left\{{}\begin{matrix}\dfrac{b^3}{c+2a}+\dfrac{c+2a}{9}.b\ge\dfrac{2b^2}{3}\\\dfrac{c^3}{a+2b}+\dfrac{a+2b}{9}.c\ge\dfrac{2c^2}{3}\end{matrix}\right.\)
\(VT\ge\dfrac{2}{3}\left(a^2+b^2+c^2\right)-1\)
Mà \(a^2+b^2+c^2\ge ab+bc+ca=3\)
\(\Rightarrow VT\ge1\left(đpcm\right)\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=1\)
2. Sử dụng bất đẳng thức Cauchy-Schwarz:
\(LHS\ge\sum_{cyc}\dfrac{a^4}{ab+2ca}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{3\left(ab+bc+ca\right)}\ge\dfrac{\left(ab+bc+ca\right)^2}{3\left(ab+bc+ca\right)}=\dfrac{ab+bc+ca}{3}=\dfrac{3}{3}=1\)Vậy ta có điều phải chứng minh

A B C E D P Q O H K I
1/ E và D cùng nhìn BC dưới 2 góc bằng nhau và bằng 90 độ nên E và D cùng nằm trên đường tròn đường kính BD
=> BCDE là tứ giác nội tiếp
Xét tg vuông ABD và tg vuông ACE có
\(\widehat{ABP}=\widehat{ACQ}\) (cùng phụ với \(\widehat{BAC}\) ) (1)
\(sđ\widehat{ABP}=\dfrac{1}{2}sđ\) cung AP (góc nội tiếp) (2)
\(sđ\widehat{ACQ}=\dfrac{1}{2}sđ\) cung AQ (góc nội tiếp) (3)
Từ (1) (2) (3) => sđ cung AP = sđ cung AQ
2/
Ta có
\(sđ\widehat{ABP}=\dfrac{1}{2}sđ\) cung AP (góc nt) (1)
\(sđ\widehat{ABQ}=\dfrac{1}{2}sđ\) cung AQ (góc nt) (2)
Mà sđ cung AP = sđ cung AQ (cmt) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ABP}=\widehat{ABQ}\) => BA là phân giác của \(\widehat{PBQ}\)
Mà \(AB\perp CQ\) => BA là đường cao của tg HBQ
=> tg HBQ cân tại B (trong tg đường phân giác đồng thời là đường cao thì tg đó là tg cân)
=> EQ=EH (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến) => E là trung điểm của HQ (đpcm)
Chứng minh tương tự ta cũng có D là trung điểm của HP
=> ED là đường trung bình của tg HPQ => ED//PQ
Nối AO cắt (O) tại K ta có
sđ cung AQK = sđ cung APK (nửa đường tròn)
sđ cung AQ = sđ cung AP (cmt)
=> sđ cung QBK = sđ cung PCK => KQ=KP (hai cung có số đo bằng nhau thì hai dây trương cung tương ứng có độ dài bằng nhau) => tg KPQ cân tại K
Ta có
\(sđ\widehat{AKQ}=\dfrac{1}{2}sđ\) cung AQ (góc nt)
\(sđ\widehat{AKP}=\dfrac{1}{2}sđ\) cung AP (góc nt)
Mà sđ cung AQ = sđ cung AP (cmt)
=> \(\widehat{AKQ}=\widehat{AKP}\) => AK là phân giác \(\widehat{PKQ}\) của tg cân KPQ
=> AK là đường cao của tg KPQ (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
\(\Rightarrow AK\perp PQ\Rightarrow OA\perp PQ\) mà DE//PQ (cmt) \(\Rightarrow OA\perp DE\) (đpcm)
3/ Ta có
Xét tg vuông ABD có
\(\widehat{ABD}=90^o-\widehat{CAB}=90^o-60^o=30^o\)
\(\Rightarrow AD=\dfrac{AB}{2}\) (trong tg vuông cạnh đối diện với góc \(30^o\) bằng nửa cạnh huyền)
C/m tương tự khi xét tg vuông ACE ta cũng có \(AE=\dfrac{AC}{2}\)
Ta có
\(sđ\widehat{ADB}=30^o=\dfrac{1}{2}sđ\) cung AP => sđ cung AP\(=60^o\) = sđ cung AQ
Gọi I là giao của AK với PQ ta có
tg KPQ cân tại K (cmt)
\(AK\perp PQ\) (cmt)
=> IQ=IP (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)
Xét tg vuông AQI có
\(sđ\widehat{AQI}=\dfrac{1}{2}sđ\) cung AP = \(30^o\Rightarrow AI=\dfrac{AQ}{2}\) (trong tg vuông cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)
Ta có \(\widehat{AQK}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông AQK có
\(AQ^2=AI.AK=\dfrac{AQ}{2}.2R\Rightarrow AQ=R\Rightarrow AI=\dfrac{AQ}{2}=\dfrac{R}{2}\)
\(\Rightarrow IK=AK-AI=2R-\dfrac{R}{2}=\dfrac{3R}{2}\)
Ta có
\(IQ^2=IA.IK\) (trong tg vuông bình phươn đường cạo hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow IQ^2=\dfrac{R}{2}.\dfrac{3R}{2}\Rightarrow IQ=\dfrac{R\sqrt{3}}{2}\)
Ta có
IQ=IP (cmt) => PQ=2.IQ=\(R\sqrt{3}\)
Ta có ED là đường trung bình của tg HPQ (cmt)
\(\Rightarrow DE=\dfrac{PQ}{2}=\dfrac{R\sqrt{3}}{2}\)
Ta có
\(S_{ABC}=\dfrac{1}{2}.AB.AC.\sin\widehat{CAB}=\dfrac{1}{2}.AB.AC.\dfrac{\sqrt{3}}{2}=\dfrac{AB.AC.\sqrt{3}}{4}\)
\(S_{AED}=\dfrac{1}{2}.AD.AE.\sin\widehat{CAB}=\dfrac{1}{2}.\dfrac{AB}{2}.\dfrac{AC}{2}.\dfrac{\sqrt{3}}{2}=\dfrac{AB.AC.\sqrt{3}}{16}\)
\(\Rightarrow\dfrac{S_{AED}}{S_{ABC}}=\dfrac{1}{4}\)
Gọi R' là bán kính đường tròn ngoại tiếp tg AED
\(S_{AED}=\dfrac{AE.AD.DE}{4R'}=\dfrac{AC}{2}.\dfrac{AB}{2}.\dfrac{6\sqrt{3}}{2}.\dfrac{1}{4R'}=\dfrac{AB.AC.\sqrt{3}}{4}.\dfrac{3\sqrt{3}}{4R'}=\dfrac{S_{ABC}.3\sqrt{3}}{4R'}\)
\(\Rightarrow\dfrac{S_{AED}}{S_{ABC}}=\dfrac{3\sqrt{3}}{4R'}=\dfrac{1}{4}\Rightarrow R'=3\sqrt{3}\)

`ĐK: y > -5`
Đặt `(x-2)^2=a` ; `1/\sqrt{y+5}=b` `(a >= 0)` khi đó hệ ptr có dạng:
`{(2a+b=3),(a-2b=-1):}`
`<=>{(4a+2b=6),(a-2b=-1):}`
`<=>{(5a=5),(a-2b=-1):}`
`<=>{(a=1),(1-2b=-1):}`
`<=>{(a=1),(b=1):}` (t/m)
`=>{((x-2)^2=1),(1/\sqrt{y+5}=1):}`
`<=>{(|x-2|=1),(\sqrt{y+5}=1):}`
`<=>{(x=3\text{ hoặc }x=1),(y+5=1<=>y=-4\text{ (t/m)}):}`
Vậy hệ ptr có tập nghiệm `S={(3;-4),(1;-4)}`

1. Khi $m=4$ thì phương trình trở thành $x^2-9x+20=0\Leftrightarrow (x-4)(x-5)=0$ hay $x=4$ hoặc $x=5$ là các nghiệm của phương trình.
2. Ta có \(\Delta=\left(2m+1\right)^2-4\left(m^2+m\right)=1>0\) nên phương trình luôn có 2 nghiệm phân biệt, hơn thế nữa ta có $x^2-(2m+1)x+m^2+m=0$ có 2 nghiệm là $x_1,x_2$ thì theo định lý Viete ta có $x_1+x_2=2m+1,x_1.x_2=m^2+m$, ta có $-17=(x_1+x_2)^2-7x_1.x_2=(2m+1)^2-7(m^2+m)$ hay $-3m^2-3m+18=0\Leftrightarrow 3(m+3)(m-2)=0$, vậy $m=2,m=-3$ là các giá trị cần tìm

A B C F K O E
a/ Ta có B và C cùng nhìn AO dưới 1 góc vuông nên B và C cùng nằm trên đường tròn đường kính AO => ABOC là tứ giác nội tiếp
b/
Xét tg ABF và tg AKB có
\(\widehat{BAK}\) chung
\(sđ\widehat{ABF}=\dfrac{1}{2}sđ\) cung BF (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{AKB}=\dfrac{1}{2}sđ\) cung BF (góc nội tiếp)
\(\Rightarrow\widehat{ABF}=\widehat{AKB}\)
=> tg ABF đồng dạng với tg AKB (g.g.g)
\(\Rightarrow\dfrac{AB}{AK}=\dfrac{BF}{BK}\) (1)
Tương tự ta cũng c/m được tg ACF đồng dạng với tg AKC
\(\Rightarrow\dfrac{AC}{AK}=\dfrac{CF}{CK}\) (2)
Mà AB=AC (hai tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{BF}{BK}=\dfrac{CF}{CK}\Rightarrow BF.CK=CF.BK\) (đpcm)
c/
Xét tg FCE và tg BCE có
\(\widehat{BEC}\) chung
\(sđ\widehat{FCE}=\dfrac{1}{2}sđ\) cung CF (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{EBC}=\dfrac{1}{2}sđ\) cung CF (góc nội tiếp)
\(\Rightarrow\widehat{FCE}=\widehat{EBC}\)
=> tg FCE đồng dạng với tg BCE (g.g.g)

Barn hợp đồng là : Công ty phải sản xuất M thùng trong N ngày.
X thùng trong 1 ngày của xí nghiệp chạy binh thường.
theo quy định là tới ngày n giao hàng theo yêu cầu
( X + 35 ) ( N - 3 ) = M
Ngày giao là ngày thứ N thì số thùng sẽ là
M : ( N - 3) - 35

\(\left\{{}\begin{matrix}\left(x^2-2x-9\right)\sqrt{x^2-x-6}=0\left(1\right)\\x+y=0\left(2\right)\end{matrix}\right.\)
ĐK: \(\left[{}\begin{matrix}x\ge3\\x\le-2\end{matrix}\right.\)
Từ (1) <=> \(\left[{}\begin{matrix}x^2-2x-9=0\left(\cdot\right)\\x^2-x-6=0\end{matrix}\right.\) (*) nghiệm không tm đk
<=> \(\left[{}\begin{matrix}x=3\left(I\right)\\x=-2\left(II\right)\end{matrix}\right.\) ->
Từ (2) => y = -x
(I) y = -3
(II) y = 2
Với x = 3 và y = -3 => P = 32 + (-3)2 + 2020 = 2038
với x = -2 và y = 2 => P = (-2)2 + 22 + 2020 = 2028
cho mn hỏi là (*) tìm ra nghiệm là \(x=1-\sqrt{10}=-2,1622....\) và \(x=1+\sqrt{10}=4,1622.....\)
tại sao lại bị loại vậy (dựa vào ĐKXĐ kiểu j mà bị loại), mn ko rõ lắm
câu 27
\(\sqrt{\dfrac{200}{176^2-112^2}}\)
= \(\sqrt{\dfrac{200}{\left(176-112\right)\left(176+112\right)}}\)
= \(\sqrt{\dfrac{200}{64\times288}}\)
= \(\dfrac{10\sqrt{2}}{8\times12\sqrt{2}}\)
= \(\dfrac{5}{48}\)