\(D=\dfrac{\left|x\right|+2023}{\left|x\right|+2022}=\dfrac{\left|x\right|+2022}{\left|x\right|+2022}+\dfrac{1}{\left|x\right|+2022}\\ =1+\dfrac{1}{\left|x\right|+2022}\)

Nhận thấy : \(\left|x\right|\ge0\forall x\inℝ\)

\(\Rightarrow\left|x\right|+2022\ge2022\)

\(\Rightarrow\dfrac{1}{\left|x\right|+2022}\le\dfrac{1}{2022}\)

\(\Rightarrow D=1+\dfrac{1}{\left|x\right|+2022}\le1+\dfrac{1}{2022}=\dfrac{2023}{2022}\)

Dấu = xảy ra khi : \(\left|x\right|=0\Rightarrow x=0\)

Vậy GTLN của D là : \(\dfrac{2023}{2022}\) tại x=0

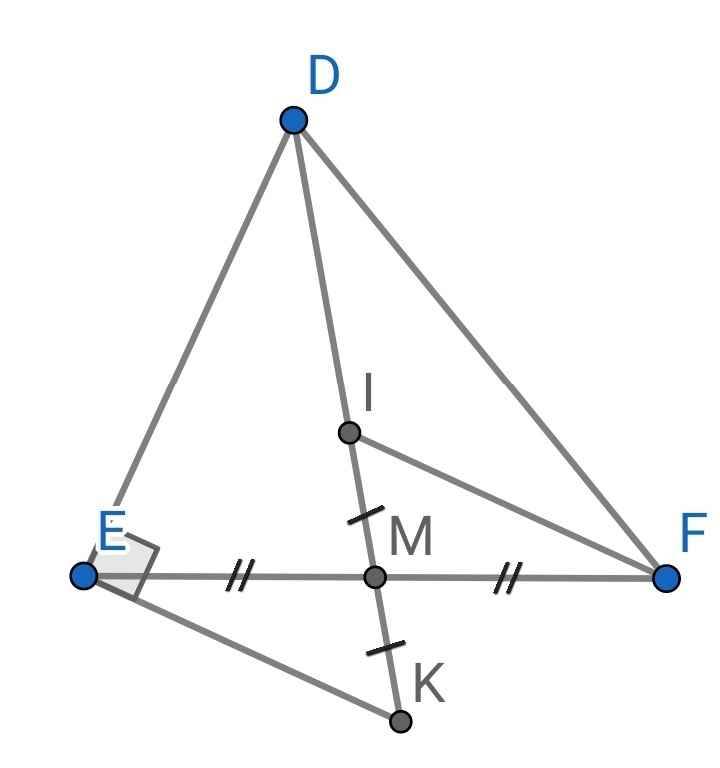 a) Do M là trung điểm của EF (gt)

⇒ ME = MF

Xét ∆EMK và ∆FMI có:

ME = MF (cmt)

∠EMK = ∠FMI (đối đỉnh)

MK = MI (gt)

⇒ ∆EMK = ∆FMI (c-g-c)

b) Do ∆EMK = ∆FMI (gt)

⇒ ∠MEK = ∠MFI (hai góc tương ứng)

Mà ∠MEK và ∠MFI là hai góc so le trong

⇒ EK // FI

Mà EK ⊥ DE (gt)

⇒ FI ⊥ DE

2/3 số ngày dự định là:

45 × 2/3 = 30 (ngày)

Do năng suất của mỗi người là như nhau và cùng làm một công việc nên số người và số ngày là hai đại lượng tỉ lệ nghịch

Số công nhân hoàn thành ngôi nhà trong 30 ngày:

45 . 20 : 30 = 30 (người)

Số công nhân cần bổ sung:

30 - 20 = 10 (người)

(\(\dfrac{2}{3}\) + \(x\)) : \(\dfrac{4}{3}\) = - \(\dfrac{1}{12}\)

  \(\dfrac{2}{3}\) + \(x\)       = - \(\dfrac{1}{12}\) x \(\dfrac{4}{3}\)

   \(\dfrac{2}{3}\) + \(x\)     = - \(\dfrac{1}{9}\)

           \(x\)    = - \(\dfrac{1}{9}\) - \(\dfrac{2}{3}\)

           \(x\)  = - \(\dfrac{7}{9}\)

Vì AB=AC=> Tam giác ABC cân tại A

+) Tam giác ABC cân tại A có AM là tpg góc BAC

=> AM đồng thời là đường cao và đường trung tuyến

a) Do AM là đường trung tuyến 

=> M là trung điểm BC

b) Do AM là đường cao

=> AM\(\perp\)BC

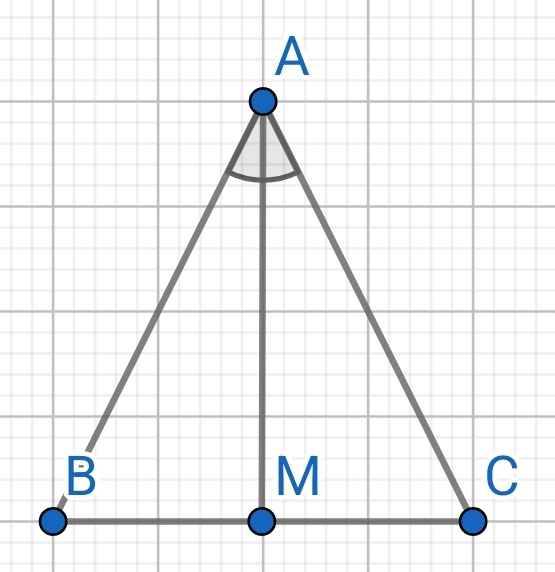 a) Do AM là tia phân giác của ∠BAC (gt)

⇒ ∠BAM = ∠CAM

Xét ∆ABM và ∆ACM có:

AM là cạnh chung

∠BAM = ∠CAM (cmt)

AB = AC (gt)

⇒ ∆ABM = ∆ACM (c-g-c)

⇒ BM = CM (hai cạnh tương ứng)

⇒ M là trung điểm của BC

b) Do ∆ABM = ∆ACM (cmt)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180⁰ (kề bù)

⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BC

81 = x³

x = ∛81

x = 3∛3

5ˣ⁺² - 5ˣ = 20

5ˣ(5² - 1) = 20

5ˣ.24 = 20

5ˣ = 20/24

5ˣ = 5/6

Em xem lại đề nhé!

\(3.\left(x-\dfrac{1}{2}\right)^3=81\\ =>\left(x-\dfrac{1}{2}\right)^3=81:3=27\\ =>x-\dfrac{1}{2}=3\\ =>x=3+\dfrac{1}{2}=\dfrac{7}{2}\)

3.(x - 1/2)³ = 81

(x - 1/2)³ = 81 : 3

(x - 1/2)³ = 27

(x - 1/2)³ = 3³

x - 1/2 = 3

x = 3 + 1/2

x = 7/2