Bài 1:

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có

AB=AC

\(\widehat{BAH}\) chung

Do đó: ΔAHB=ΔAKC

b: ΔAHB=ΔAKC

=>BH=CK

Xét ΔKBC vuông tại K và ΔHCB vuông tại H có

BC chung

KC=HB

Do đó: ΔKBC=ΔHCB

=>\(\widehat{IBC}=\widehat{ICB}\)

=>IB=IC

=>I nằm trên đường trung trực của BC(1)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra AI là đường trung trực của BC

Bài 3:

a: Xét ΔHEB vuông tại E và ΔHFC vuông tại F có

HB=HC

\(\widehat{HBE}=\widehat{HCF}\)

Do đó; ΔHEB=ΔHFC

b: Xét ΔAMK có

MF,KE là các đường cao

MF cắt KE tại H

Do đó: H là trực tâm của ΔAMK

=>AH\(\perp\)MK

Gọi số quyển tập ba lớp 7A,7B,7C quyên góp được lần lượt là a(quyển),b(quyển),c(quyển)

(Điều kiện: \(a,b,c\in Z^+\))

Số quyển tập ba lớp quyên góp được lần lượt tỉ lệ với 7;3;4 nên \(\dfrac{a}{7}=\dfrac{b}{3}=\dfrac{c}{4}\)

Tổng số quyển tập ba lớp quyên góp được là 420 nên a+b+c=420

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{7}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{7+3+4}=\dfrac{420}{14}=30\)

=>\(a=30\cdot7=210\left(nhận\right);b=3\cdot30=90\left(nhận\right);c=4\cdot30=120\left(nhận\right)\)

vậy: số quyển tập ba lớp 7A,7B,7C quyên góp được lần lượt là 210(quyển),90(quyển),120(quyển)

Gọi số tiền đơn vị 1,2,3 đóng góp lần lượt là a(triệu),b(triệu),c(triệu)

(Điều kiện: a>0; b>0; c>0)

Số tiền đóng góp của 3 đơn vị lần lượt tỉ lệ với 3;5;8 nên \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\)

Tổng số tiền lãi là 256 triệu nên a+b+c=256

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{3+5+8}=\dfrac{256}{16}=16\)

=>\(a=16\cdot3=48;b=16\cdot5=80;c=16\cdot8=128\)

vậy: Số tiền ba đơn vị đóng góp lần lượt là 48 triệu; 80 triệu; 128 triệu

\(E\left(x\right)=2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=-\dfrac{1}{2}\)

Vậy \(x=-\dfrac{1}{2}\) là nghiệm của đa thức

\(E\left(x\right)=0\Rightarrow2x+1=0\)

\(\Rightarrow2x=-1\)

\(\Rightarrow x=\dfrac{-1}{2}\)

Vậy...

a: Xét ΔBAH và ΔBDH có

BA=BD

AH=DH

BH chung

Do đó: ΔBAH=ΔBDH

b: ΔBAH=ΔBDH

=>\(\widehat{ABH}=\widehat{DBH}\)

Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

=>EA=ED

=>ΔEAD cân tại E

c: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ACB}=30^0\)

Xét ΔEDC vuông tại D có \(sinECD=\dfrac{ED}{EC}\)

=>\(\dfrac{EA}{EC}=sin30=\dfrac{1}{2}\)

=>EC=2AE

vẽ hình nx nhé bạn

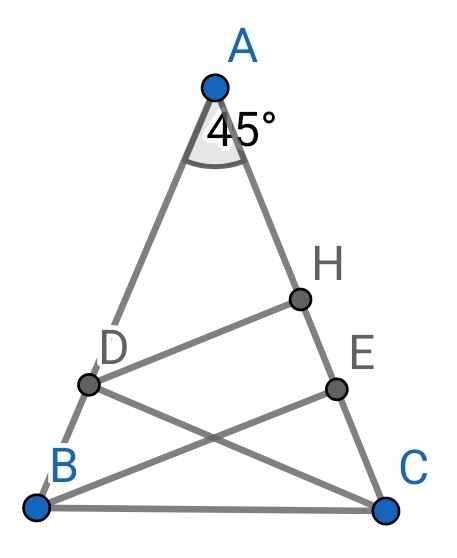
a) Do ∆ABC cân tại A (gt)

⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2

= (180⁰ - 45⁰) : 2

= 67,5⁰

Do ∠ABC = ∠ACB > ∠BAC (67,5⁰ = 67,5⁰ > 45⁰)

⇒ AC = AB > BC

b) Do ∠ABC = ∠ACB (cmt)

⇒ ∠DBC = ∠ECB

Xét ∆BCD và ∆CBE có:

BD = CE (gt)

∠DBC = ∠ECB (cmt)

BC là cạnh chung

⇒ ∆BCD = ∆CBE (c-g-c)

⇒ ∠BDC = ∠CEB (hai góc tương ứng)

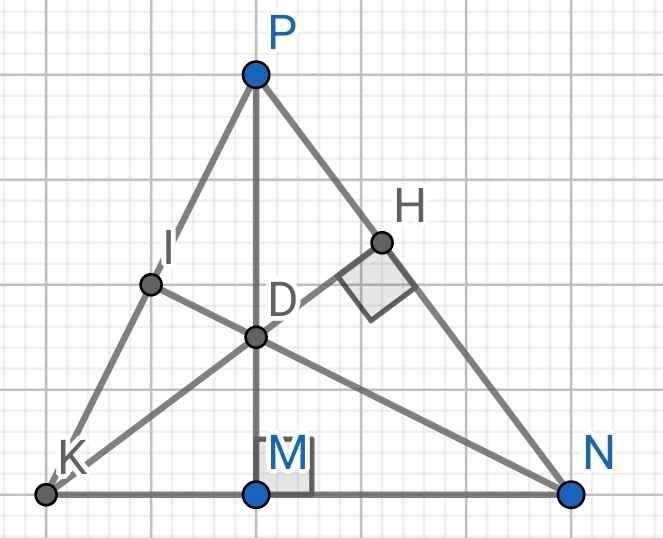
a) Do ND là đường phân giác của ∆MNP (gt)

⇒ ∠MND = ∠PND

⇒ ∠MND = ∠HND

Xét hai tam giác vuông: ∆MND và ∆HND có:

ND là cạnh chung

∠MND = ∠HND (cmt)

⇒ ∆MND = ∆HND (cạnh huyền - góc nhọn)

b) Do ∆MND = ∆HND (cmt)

⇒ MN = HN (hai cạnh tương ứng)

c) Do ∆MND = ∆HND (cmt)

⇒ MD = HD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆DMK và ∆DHP có:

MD = HD (cmt)

∠MDK = ∠HDP (đối đỉnh)

⇒ ∆DMK = ∆DHP (cạnh góc vuông - góc nhọn kề)

⇒ MK = HP (hai cạnh tương ứng)

Lại có: MN = HN (cmt)

⇒ MK + MN = HP + HN

⇒ KN = PN

⇒ ∆NPK cân tại N

Do ∆MNP vuông tại M (gt)

⇒ PM ⊥ MN

⇒ PM ⊥ NK

⇒ PM là đường cao của ∆NPK

Lại có:

DH ⊥ NP (gt)

⇒ KH ⊥ NP

⇒ KH là đường cao thứ hai của ∆NPK

⇒ ND là đường cao thứ ba của ∆NPK

Mà ∆NPK cân tại N (cmt)

⇒ ND cũng là đường trung tuyến của ∆NPK

⇒ ND đi qua trung điểm của PK

Mà I là trung điểm của PK

⇒ N, D, I thẳng hàng

a: A(x)+B(x)

\(=8x^4+8x^3-6x-15+8x^4+8x^3-4x^2-6x-10\)

\(=16x^4+16x^3-4x^2-12x-25\)

b: B(x)-A(x)

\(=8x^4+8x^3-4x^2-6x-10-8x^4-8x^3+6x+15\)

\(=-4x^2+5\)

c: \(C\left(x\right)\cdot\left(B\left(x\right)-A\left(x\right)\right)=\left(x+1\right)\left(-4x^2+5\right)\)

\(=-4x^3+5x-4x^2+5\)

Công thức tính diện tích đáy của hình lăng trụ đứng còn tùy thuộc xem đáy của hình lăng trụ đứng đó là hình gì em nhé.

+ Nếu đáy là hình tam giác sử dụng công thức tính diện tích hình tam giác

+ Nếu đáy là hình chữ nhật sử dụng công thức tính diện tích hình chữ nhật

+ Nếu đáy là hình thang sử dụng công thức tính diện tích hình thang.

+ Nếu đáy là hình tròn sử dụng công thức tính diện tích hình tròn.

+ Nếu đáy là hình vuông sử dụng công thức tính diện tích hình vuông.

+ Nếu đáy là hình thoi sử dụng công thức tính diện tích hình thoi.

+ Nếu đáy là bình hành thì sử dụng công thức tính diện tích hình bình hành.

+ Nếu đáy là hình khác biệt thì chia đáy đó thành hình thông thường, tính diện tích từng hình, cộng tất cả diện tích các hình thông thường đó ta được diện tích đáy. 

Công thức tính diện tích đáy của hình lăng trụ đứng còn tùy thuộc xem đáy của hình lăng trụ đứng đó là hình gì em nhé.

+ Nếu đáy là hình tam giác sử dụng công thức tính diện tích hình tam giác

+ Nếu đáy là hình chữ nhật sử dụng công thức tính diện tích hình chữ nhật

+ Nếu đáy là hình thang sử dụng công thức tính diện tích hình thang.

+ Nếu đáy là hình tròn sử dụng công thức tính diện tích hình tròn.

+ Nếu đáy là hình vuông sử dụng công thức tính diện tích hình vuông.

+ Nếu đáy là hình thoi sử dụng công thức tính diện tích hình thoi.

+ Nếu đáy là bình hành thì sử dụng công thức tính diện tích hình bình hành.

+ Nếu đáy là hình khác biệt thì chia đáy đó thành hình thông thường, tính diện tích từng hình, cộng tất cả diện tích các hình thông thường đó ta được diện tích đáy.