(x-5)^3:(-2)=4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c)
= 10 . 1/10 . 4/3 + 3.7 - 1/6 . 2
= 4/3 + 21 - 1/3
= (4/3 - 1/3) + 21
= 1 + 21
= 22


Lời giải:
Ta thấy:
$|5a-6b+300|^{2011}\geq 0, \forall a,b$ (tính chất trị tuyệt đối)
$(2a-3b)^{2022}\geq 0, \forall a,b$
Do đó để tổng của chúng bằng $0$ thì:
$|5a-6b+300|=2a-3b=0$
$\Leftrightarrow 5a-6b=-300(*)$ và $2a=3b$
$2a=3b\Rightarrow a=1,5b$. Thay vào đk $(*)$ thì:
$5.1,5b-5b=-300$
$\Rightarrow 7,5b-5b=-300$
$\Rightarrow 2,5b=-300\Rightarrow b=-120$
$a=1,5b=1,5(-120)=-180$

a, \(\sqrt{x-2}\) = 5 (đk \(x\) - 2 ≥ 0; \(x\ge2\))
\(x-2=25\)
\(x\) = 25 + 2
\(x\) = 27

Lời giải:
$=\frac{2}{5}\times \frac{2}{9}+\frac{2}{5}\times \frac{7}{9}+2\frac{3}{5}$
$=\frac{2}{5}\times (\frac{2}{9}+\frac{7}{9})+2+\frac{3}{5}$
$=\frac{2}{5}\times 1+2+\frac{3}{5}=\frac{2}{5}+\frac{3}{5}+2=1+2=3$

Trước tiên, ta chứng minh \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\) với \(a,b>0\) (*)
(*) \(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+2ab+b^2\ge4ab\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\), luôn đúng.
Vậy (*) được chứng minh. Dấu "=" xảy ra \(\Leftrightarrow a=b\)
\(\Rightarrow VT=a+b+\dfrac{1}{a}+\dfrac{1}{b}\ge a+b+\dfrac{4}{a+b}\)
Đặt \(a+b=t\left(0< t\le\dfrac{1}{2}\right)\)thì
\(VT\ge t+\dfrac{4}{t}\) \(=t+\dfrac{1}{4t}+\dfrac{15}{4t}\) (1)
Bây giờ ta sẽ chứng minh \(a+b\ge2\sqrt{ab}\) với \(a,b>0\) (**)
(**) \(\Leftrightarrow a-2\sqrt{ab}+b\ge0\)
\(\Leftrightarrow\left(\sqrt{a}\right)^2-2\sqrt{a}\sqrt{b}+\left(\sqrt{b}\right)^2\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) (luôn đúng)
Vậy (**) được chứng minh. Dấu "=" xảy ra \(\Leftrightarrow a=b\)
Do đó từ (1) \(\Rightarrow VT\ge\left(t+\dfrac{1}{4t}\right)+\dfrac{15}{4t}\)
\(\ge2\sqrt{t.\dfrac{1}{4}t}+\dfrac{15}{4.\dfrac{1}{2}}\) (do \(0< t\le\dfrac{1}{2}\))
\(=\dfrac{17}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}t=a+b=\dfrac{1}{2}\\a=b\end{matrix}\right.\Leftrightarrow a=b=\dfrac{1}{4}\)
Ta có đpcm.

Lời giải:
$2023xy+2024yz+4047xz=2023xy+2024y(-x-y)+4047x(-x-y)$
$=-2024y^2-4047x^2-4048xy$
$=-[4047x^2+2024y^2+4048xy]$
$=-[2024(x^2+y^2+2xy)+2023x^2]=-[2024(x+y)^2+2023x^2]$
Vì $2024(x+y)^2+2023x^2\geq 0$ với mọi $x,y$
$\Rightarrow -[2024(x+y)^2+2023x^2]\leq 0$ với mọi $x,y$
Do đó nó không thể nhận giá trị dương.
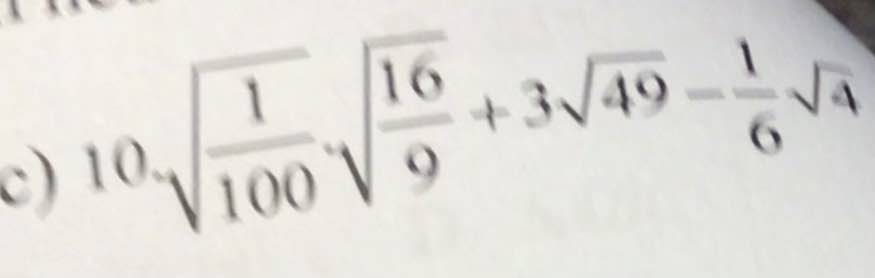

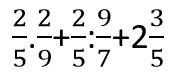
(\(x-5\))3 : (-2) = 4
(\(x-5\))3 = 4 x (-2)
(\(x-5\))3 = - 8
(\(x-5\))3 = (-2)3
\(x-5\) = - 2
\(x\) = - 2 + 5
\(x\) = 3