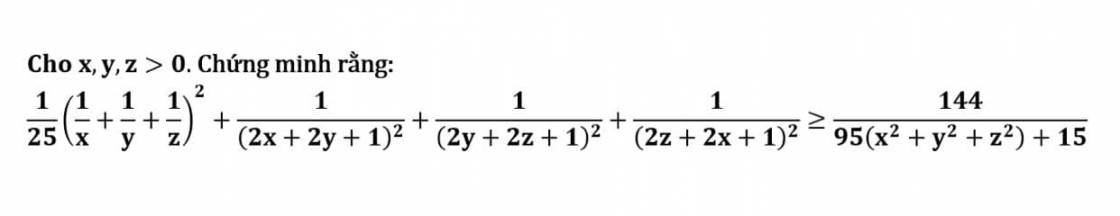Cho \(\Delta ABC\) nhọn nội tiếp trong đường tròn tâm O bán kính R. Chứng minh chu vi \(\Delta ABC\) > 4R.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
a + b + c = 0
<=> a2 + b2 + c2 + 2(ab + bc + ac) = 0
<=> ab + bc + ac = -7
<=> a2b2 + b2c2 + a2c2 + 2abc(a + b + c) = 49
<=> a2b2 + b2c2 + a2c2 = 49 (vì a + b + c = 0)
<=> 2(a2b2 + b2c2 + a2c2) = 98
<=> (a2 + b2 + c2)2 = 98 + a4 + b4 + c4
<=> a4 + b4 + c4 = 142 - 98 = 98

\(x-2\sqrt{x-1}=16\)
Điều kiện: \(x\ge1\)
\(\Leftrightarrow\left(x-1\right)-2\sqrt{x-1}+1=16\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2=16\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2=\left(\pm4\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}-1=4\\\sqrt{x-1}=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=5\\\sqrt{x-1}=-3\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left(\sqrt{x-1}\right)^2=5^2\)
\(\Leftrightarrow x=26\)

\(\Sigma\dfrac{1}{\sqrt[3]{x\left(y+z\right)}}\ge\dfrac{9}{\sqrt[3]{x\left(y+z\right)}+\sqrt[3]{y\left(x+z\right)}+\sqrt[3]{\left(z\left(x+y\right)\right)}}=\dfrac{9\sqrt[3]{4}}{\sqrt[3]{4}.\Sigma\sqrt[3]{x\left(y+z\right)}}\)
\(có:\sqrt[3]{4}\sqrt[3]{x\left(y+z\right)}=\sqrt[3]{2.2x.\left(y+z\right)}\le\dfrac{2+2x+y+z}{3}\)
\(tương\) \(tự\Rightarrow\Sigma\dfrac{1}{\sqrt[3]{x\left(y+z\right)}}\ge\dfrac{9.\sqrt[3]{4}}{\dfrac{2+2x+y+z}{3}+\dfrac{2+2y+x+z}{3}+\dfrac{2+2z+x+y}{3}}=\dfrac{27\sqrt[3]{4}}{6+4\left(x+y+z\right)}\ge\dfrac{27.\sqrt[3]{4}}{6+4\sqrt{3\left(x^2+y^2+z^2\right)}}=\dfrac{27\sqrt[3]{4}}{6+4\sqrt{3.3}}=\dfrac{3}{\sqrt[3]{2}}\)
\(dấu"="\Leftrightarrow x=y=z=1\)

\(\dfrac{AB}{AC}=\dfrac{5}{6}\Leftrightarrow AB=\dfrac{5}{6}AC\)
\(BC^2=AB^2+AC^2=\left(\dfrac{5}{6}AC\right)^2+AC^2=\dfrac{61}{36}AC^2\)
\(\Rightarrow AC^2=8784\Rightarrow AC=12\sqrt{61}\Rightarrow AB=10\sqrt{61}\)
\(BD\) là phân giác của giác của \(\widehat{ABC}\) suy ra
\(\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{AD+CD}{AB+BC}=\dfrac{AC}{AB+BC}=\dfrac{12\sqrt{61}}{10\sqrt{61}+122}=\dfrac{\sqrt{61}-5}{6}\)
\(\Rightarrow AD=\dfrac{\sqrt{61}-5}{6}.10\sqrt{61}=\dfrac{5}{3}\left(61-5\sqrt{61}\right)\)

Dựng hình vuông \(BCEF\). Lấy \(M\) thuộc \(BF\) sao cho \(PM=PQ\) khi đó suy ra \(MF=QA\).
\(\Delta BCM=\Delta DCQ\left(c.g.c\right)\) suy ra \(\widehat{BCM}=\widehat{DCQ}\)
suy ra \(\widehat{QCM}=\widehat{QCB}+\widehat{BCM}=\widehat{QCM}+\widehat{DCQ}=\widehat{DCB}=90^o\)
\(\Delta CPQ=\Delta CPM\left(c.c.c\right)\) suy ra \(\widehat{PCQ}=\widehat{PCM}\)
suy ra \(\widehat{PCQ}=\dfrac{1}{2}\widehat{QCM}=45^o\)

điều kiện để \(\sqrt{-x^2-3}\) có nghĩa thì
-x2 - 3 ≥ 0
⇔ x2 + 3 ≤ 0
ta có x2 ≥ 0 ⇔ x2 + 3 ≥ 0 ∀ x ϵ R
vậy không có giá trị nào của x để biểu thức trong căn có nghĩa

vì 2x2 ≥ 0 ⇒ 2x2 + 1 ≥ 1 ∀ x ϵ R
vậy \(\sqrt{2x^2+1}\) + \(\dfrac{2}{3}\) - 2x xác định ∀ x ϵ R

Lời giải:
Biểu thức xác định khi $2x^2+1\geq 0$ (luôn đúng với mọi $x\in\mathbb{R}$ do $2x^2+1\geq 2.0+1>0$ với mọi $x\in\mathbb{R}$)

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(\text{VT}\geq \frac{1}{25}.\frac{81}{(x+y+z)^2}+\frac{1}{(2x+2y+1)^2}+\frac{1}{(2y+2z+1)^2}+\frac{1}{(2z+2x+1)^2}\)
\(=\frac{9^2}{25(x+y+z)^2}+\frac{1}{(2x+2y+1)^2}+\frac{1}{(2y+2z+1)^2}+\frac{1}{(2z+2x+1)^2}\)
\(\geq \frac{(9+1+1+1)^2}{25(x+y+z)^2+\sum (2x+2y+1)^2}=\frac{144}{25(x+y+z)^2+\sum (2x+2y+1)^2}\)
\(=\frac{144}{25.3(x^2+y^2+z^2)+\sum (2x+2y+1)^2}\)
Ta cần cm $\sum (2x+2y+1)^2\leq 20(x^2+y^2+z^2)+15$
$\Leftrightarrow 8(x^2+y^2+z^2)+8(xy+yz+xz)+8(x+y+z)+3\leq 20(x^2+y^2+z^2)+15$
$\Leftrightarrow 3(x^2+y^2+z^2)+3\geq 2(xy+yz+xz)+2(x+y+z)$
$\Leftrightarrow (x-y)^2+(y-z)^2+(z-x)^2+(x-1)^2+(y-1)^2+(z-1)^2\geq 0$ (luôn đúng với mọi $x\in\mathbb{R}^+$)
Do đó ta có đpcm
Dấu "=" xảy ra khi $x=y=z=1$