Cho tam giác ABC có c^h-2a^2c^2-2b^2c^2+a^2+a^2b^2+b^4. Tính cos C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\sqrt{1+\cot^2x+4\left(1+\tan^2x\right)-9}\)
(dùng \(\dfrac{1}{\sin^2x}=1+\cot^2x\) và \(\dfrac{1}{\cos^2x}=1+\tan^2x\))
\(A=\sqrt{4\tan^2x+\cot^2x-4}\)
\(A=\sqrt{4\tan^2x-4\tan x\cot x+\cot^2x}\) (do \(\tan x\cot x=1\))
\(A=\sqrt{\left(2\tan x-\cot x\right)^2}\)
\(A=\sqrt{m^2}\)
\(A=\left|m\right|\)
\(\Rightarrow\) Chọn B

Gọi chung 2 KL cần tìm là A.
PT: \(2A+2HCl\rightarrow2ACl+H_2\)
\(n_{H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
Theo PT: \(n_A=2n_{H_2}=0,6\left(mol\right)\)
\(\Rightarrow\overline{M}_A=\dfrac{18,6}{0,6}=31\left(g/mol\right)\)
Mà: 2 KL ở 2 chu kì kế tiếp nhau.
→ Na và K


Áp dụng định lý cosin cho tam giác ABC, ta được:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}\)
\(=\sqrt{21^2+16^2-2.21.16.cos60^o}\)
\(=19\)
Do đó \(p=\dfrac{AB+BC+CA}{2}=\dfrac{21+16+19}{2}=28\)
Mà \(S_{ABC}=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.21.16.sin60^o=84\sqrt{3}\)
Mặt khác, \(S_{ABC}=pr=28r\) (\(r\) là bán kính đường tròn nội tiếp \(\Delta ABC\))
\(\Rightarrow28r=84\sqrt{3}\Leftrightarrow r=3\sqrt{3}\)

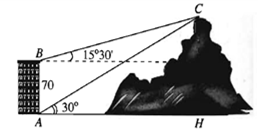
ˆABC=90°+15°30'=105°30'
Xét tam giác ABC có ˆCAB =60°, ˆABC=105°30' ta có:
ˆCAB+ˆABC+ˆACB=180° (định lí tổng ba góc trong tam giác)
⇒ˆACB=180°−ˆCAB−ˆABC
⇒ˆACB=180°−60°−105°30'=14°30'.
Áp dụng định lí sin trong tam giác ABC, ta có: ACsinˆABC=ABsinˆACB
⇒AC=AB.sinˆABCsinˆACB=70.sin105°30'sin14°30'≈269,4(m)