cho các số thực dương x y thỏa mãn x^3+y^3+x^2+y^2=2xy(x+y).Tìm GTNN của K = x ^ 3 + y ^ 3 + 3/(x ^ 2 + y ^ 2) + 2/((x + y) ^ 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Gọi chiều rộng khu vườn là $a$ (m) thì chiều dài là $3a$ (m)
Diện tích ban đầu: $a.3a=3a^2$ (m2)
Diện tích sau khi đổi: $(a+5)(3a+5)$ (m2)
Có: $(a+5)(3a+5)-3a^2=385$
$\Leftrightarrow 20a+25=385$
$\Rightarrow a=18$ (m)
Vậy chiều rộng ban đầu là 18 m và chiều dài là $18.3=54$ m

Lời giải:
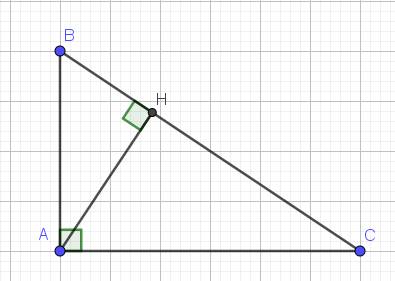
a. Xét tam giác $ABC$ và $HBA$ có:
$\widehat{B}$ chung
$\widehat{BAC}=\widehat{BHA}=90^0$
$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)
Ta có:
$AB.AC=AH.BC$ (cùng bằng 2 lần diện tích tam giác $ABC$)
b.
Xét tam giác $BHA$ và $AHC$ có:
$\widehat{BHA}=\widehat{AHC}=90^0$
$\widehat{HBA}=\widehat{HAC}$ (cùng phụ góc $\widehat{BAH}$)
$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)
$\Rightarrow \frac{BH}{HA}=\frac{AH}{HC}$
$\Rightarrow AH^2=BH.CH$.

a, Xét \(\Delta ADC\) và \(\Delta BKC\), ta có:
\(\widehat{D}\) = \(\widehat{K}\) = 90 độ
\(\widehat{C}\) chung
\(\Rightarrow\)\(\Delta ADC\) đồng dạng \(\Delta BKC\)
b, thiếu dữ kiện

Lời giải:
Gọi $H$ là chân đường cao kẻ từ $A$ xuống $BC$. Vì $ABC$ cân tại $A$ nên $H$ là trung điểm của $BC$
$\Rightarrow HB=BC:2=3$ (cm)
Áp dụng định lý Pitago: $AH=\sqrt{AB^2-HB^2}=\sqrt{5^2-3^2}=4$ (cm)
Diện tích đáy: $S_{ABC}=\frac{AH.BC}{2}=\frac{4.6}{2}=12$ (cm2)
Thể tích: $AA'.S_{ABC}=9.12=108$ (cm3)
Diện tích xung quanh: $P_{ABC}.AA'=(AB+BC+AC).AA'=(5+5+6).9=144$ (cm2)
Diện tích toàn phần: $144+2\times 12=168$ (cm2)

Lời giải:
a.
$A=\frac{3x+15}{(x-3)(x+3)}+\frac{x-3}{(x+3)(x-3)}-\frac{2(x+3)}{(x-3)(x+3)}$
$=\frac{3x+15+(x-3)-2(x+3)}{(x+3)(x-3)}=\frac{2x+6}{(x-3)(x+3)}$
$=\frac{2(x+3)}{(x-3)(x+3)}=\frac{2}{x-3}$
b.
Để $A=\frac{1}{2}$
$\Leftrightarrow \frac{2}{x-3}=\frac{1}{2}$
$\Leftrightarrow x-3=4$
$\Leftrightarrow x=7$ (tm)

Trong 1 giờ hai người cùng làm được: 1 : 10 = \(\dfrac{1}{10}\) ( công việc)
Theo bài ra ta có số ngày hai người làm chung công việc là:
6 + 3 = 9 ( ngày)
Số phần công việc hai người cùng làm trong 9 ngày là:
\(\dfrac{1}{10}\) \(\times\) 9 = \(\dfrac{9}{10}\)
Số phần công việc người thứ hai phải làm một mình trong 3 ngày là:
1 - \(\dfrac{9}{10}\) = \(\dfrac{1}{10}\) ( công việc)
Trong 1 ngày người thứ hai làm một mình được:
\(\dfrac{1}{10}\): 3 = \(\dfrac{1}{30}\) ( công việc)
Nếu làm một mình thì người thứ hai làm xong công việc sau:
1 : \(\dfrac{1}{30}\) = 30 ( ngày)
Trong 1 giờ người thứ nhất làm một mình được:
\(\dfrac{1}{10}\) - \(\dfrac{1}{30}\) = \(\dfrac{1}{15}\) ( công việc)
Người thứ nhất nếu làm một mình sẽ xong công việc sau:
1: \(\dfrac{1}{15}\) = 15 ( ngày)
Kết luận: Người thứ nhất hoàn thành công việc nếu làm một mình sau 15 ngày
Người thứ hai làm một mình sẽ xong công viêc sau 30 ngày


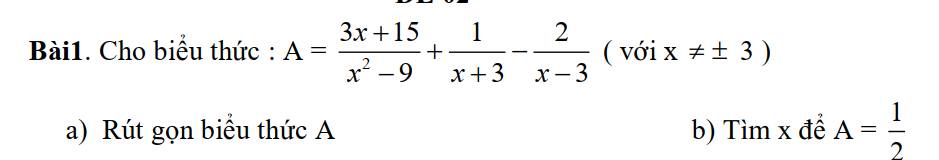
Ta có:
x^3 + y^3 + x^2 + y^2 = 2xy(x+y)
Đặt S = x + y, P = xy, ta có:
x^3 + y^3 + x^2 + y^2 = (x+y)(x^2 + y^2) = (x+y)^3 - 3xy(x+y) = S^3 - 3PS
Vậy ta có:
S^3 - 3PS + S^2 - 2P = 0
S^3 + S^2 - 3PS - 2P = S(S^2 + S - 3P) - 2P = 0
Do đó, ta có:
S^2 + S - 3P = 0
Sử dụng công thức Viết để tính nghiệm của phương trình bậc hai này, ta được:
S = (-1 + sqrt(1 + 12P))/2 hoặc S = (-1 - sqrt(1 + 12P))/2
Vì x và y là các số thực dương, nên ta chỉ quan tâm đến nghiệm dương của S, tức là:
S = (-1 + sqrt(1 + 12P))/2
Tiếp theo, ta có:
K = x^3 + y^3 + 3/(x^2 + y^2) + 2/((x+y)^2)
= S^3 - 3PS + 3/(S^2 - 2P) + 2/(S^2)
= S^3 - 3PS + 3S^2/(S^2 - 2P) + 2/(S^2)
= S^3 - 3PS + 3S^2/(S^2 - 2P) + 2S^2/(S^2 * (S^2 - 2P))
= S^3 - 3PS + (5S^4 - 6PS^2)/(S^2 * (S^2 - 2P))
= S^3 - 3PS + (5S^4 - 6PS^2)/(S^2 * (S^2 + 1 - 2xy))
= S^3 - 3PS + (5S^4 - 6PS^2)/((S^2 + 1)^2 - 2(S^2-1)P)
= S^3 - 3PS + (5S^4 - 6PS^2)/((S^2 + 1)^2 - 2(S^2-1)(S^3 - 3PS))
= S^3 - 3PS + (5S^4 - 6PS^2)/(-2S^5 + 10S^3 - 2PS^2 + 2P)
= S^3 - 3PS + (5S^4 - 6PS^2)/(2S^5 - 10S^3 + 2PS^2 - 2P)
= S^3 - 3PS + (5S^2 - 6P)/(2S^3 - 10S +