
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vận tốc lúc đi là x(km/h)
(Điều kiện: x>0)
Vận tốc lúc về là x+10(km/h)
Thời gian đi là \(\dfrac{150}{x}\left(giờ\right)\)
Thời gian về là \(\dfrac{150}{x+10}\left(giờ\right)\)
Tổng thời gian cả đi lẫn về là 5h30p=5,5 giờ nên ta có:
\(\dfrac{150}{x}+\dfrac{150}{x+10}=5,5\)
=>\(\dfrac{1}{x}+\dfrac{1}{x+10}=\dfrac{150}{5,5}=\dfrac{300}{11}\)
=>\(\dfrac{x+10+x}{x\left(x+10\right)}=\dfrac{300}{11}\)
=>300x(x+10)=11(2x+10)
=>\(300x^2+3000x-22x-110=0\)
=>\(300x^2+2978x-110=0\)(1)
\(\text{Δ}=2978^2-4\cdot300\cdot\left(-110\right)=9000484>0\)
Do đó: Phương trình (1) có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-2978-\sqrt{9000484}}{600}\left(loại\right)\\x=\dfrac{-2978+\sqrt{9000484}}{600}\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đi là \(\dfrac{-2978+\sqrt{9000484}}{600}\left(\dfrac{km}{h}\right)\)

Độ dài cạnh phần đất còn lại là 16-x(m)
Diện tích phần đất còn lại là 196m2 nên ta có:
\(\left(16-x\right)^2=196\)
=>\(\left(x-16\right)^2=196\)
=>\(\left[{}\begin{matrix}x-16=14\\x-16=-14\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=30\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Vậy: Độ dài bề rộng là 2m

Gọi số cần tìm có dạng là \(X=\overline{ab}\)
Khi viết thêm chữ số 0 vào giữa hai chữ số thì ta được số mới gấp 6 lần số cũ nên \(\overline{a0b}=6\cdot\overline{ab}\)
=>\(100a+b=6\left(10a+b\right)\)
=>100a+b=60a+6b
=>40a=5b
=>8a=b
=>b=8; a=1
Vậy: Số cần tìm là 18

Bài 2:
\(a)2x^2y-\dfrac{1}{4}x^2y+5x^2y-4x^2y\\ =x^2y\cdot\left(2-\dfrac{1}{4}+5-4\right)\\ =x^2y\cdot\left(3-\dfrac{1}{4}\right)\\ =\dfrac{11}{4}x^2y\\ b)5y^3z^2-3y^3z^2+7y^3z^2-6y^3z^2\\ =y^3z^2\cdot\left(5-3+7-6\right)\\ =3y^3z^2\\ c)-4x^3y^4+6x^2y^3+\dfrac{1}{2}x^3y^4-\dfrac{3}{2}x^2y^3\\ =\left(\dfrac{1}{2}x^3y^4-4x^3y^4\right)+\left(6x^2y^3-\dfrac{3}{2}x^2y^3\right)\\ =x^3y^4\left(\dfrac{1}{2}-4\right)+x^2y^3\left(6-\dfrac{3}{2}\right)\\ =-\dfrac{7}{2}x^3y^4+\dfrac{9}{2}x^2y^3\)

Bài 8:
1: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)
\(=2x\cdot2y=4xy\)
2: \(\left(2x+3\right)^2-3x\left(2x+1\right)\)
\(=4x^2+12x+9-6x^2-3x\)
\(=-2x^2+9x+9\)
3: \(\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\)
\(=4^2-\left(2x\right)^2-8x^2-12x\)
\(=16-4x^2-8x^2-12x=-12x^2-12x+16\)
4: \(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\)
\(=2\left(x^2-y^2\right)+x^2+2xy+y^2-2x^2\)
\(=2x^2-2y^2-x^2+2xy+y^2=x^2+2xy-y^2\)
5: \(\left(3x+4\right)\left(3x-2\right)-\left(3x+1\right)^2\)
\(=9x^2-6x+12x-8-9x^2-6x-1\)
=-9
6: \(4x\left(x-3\right)-\left(2x-1\right)\left(2x+1\right)\)
\(=4x^2-12x-\left(4x^2-1\right)\)
\(=4x^2-12x-4x^2+1=-12x+1\)
7: \(\dfrac{3}{2}x^2-\left(x-1\right)\left(x+1\right)+3x\)
\(=\dfrac{3}{2}x^2+3x-\left(x^2-1\right)\)
\(=\dfrac{3}{2}x^2+3x-x^2+1=\dfrac{1}{2}x^2+3x+1\)
8: \(2\left(5-x\right)\left(5+x\right)-\left(2x+3\right)^2-x\left(3x+2\right)\)
\(=2\left(25-x^2\right)-4x^2-12x-9-3x^2-2x\)
\(=2\left(25-x^2\right)-7x^2-14x-9\)
\(=50-2x^2-7x^2-14x-9=-9x^2-14x+41\)

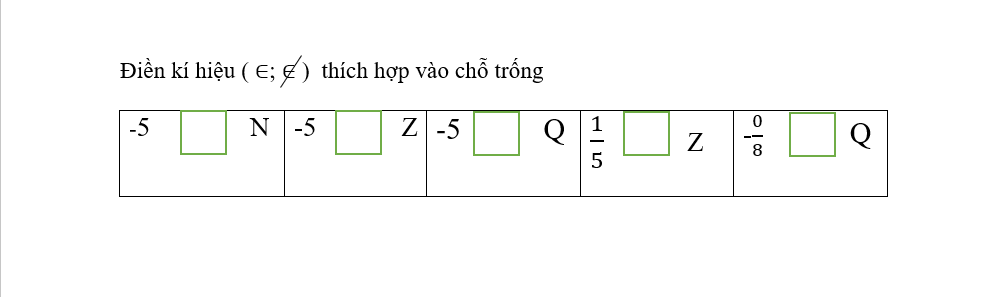
\(-5\notin N\\ -5\in Z\\- 5\in Q\\ \dfrac{1}{5}\notin Z\\ -\dfrac{0}{8}\in Q\)

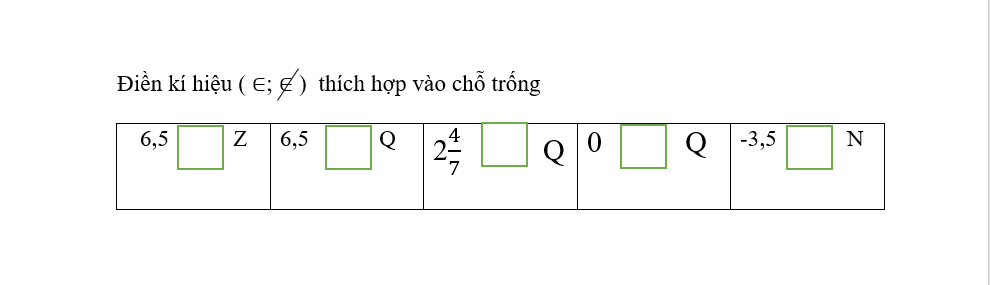
\(6,5\notin Z\\ 6,5\in Q\\ 2\dfrac{4}{7}\notin Q\\ 0\in Q\\ -3,5\notin N\)

Bài 8:
\(1)\left(x+y\right)^2-\left(x-y\right)^2\\ =\left(x^2+2xy+y^2\right)-\left(x^2-2xy+y^2\right)\\ =x^2+2xy+y^2-x^2+2xy-y^2\\ =4xy\\ 2)\left(2x+3\right)^2-3x\left(2x+1\right)\\ =\left(4x^2+12x+9\right)-\left(6x^2+3x\right)\\ =4x^2+12x+9-6x^2-3x\\ =-2x^2+9x+9\\ 3)\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\\ =\left[4^2-\left(2x\right)^2\right]-\left(8x^2+12x\right)\\ =16-4x^2-8x^2-12x\\ =16-12x^2-12x\\ 4)2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\\ =2\left(x^2-y^2\right)+\left(x^2+2xy+y^2\right)-2x^2\\ =2x^2-2y^2+x^2+2xy+y^2-2x^2\\ =x^2+2xy-y^2\)
Bài 8:
1: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)
\(=2x\cdot2y=4xy\)
2: \(\left(2x+3\right)^2-3x\left(2x+1\right)\)
\(=4x^2+12x+9-6x^2-3x\)
\(=-2x^2+9x+9\)
3: \(\left(4-2x\right)\left(4+2x\right)-4x\left(2x+3\right)\)
\(=4^2-\left(2x\right)^2-8x^2-12x\)
\(=16-4x^2-8x^2-12x=-12x^2-12x+16\)
4: \(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2-2x^2\)
\(=2\left(x^2-y^2\right)+x^2+2xy+y^2-2x^2\)
\(=2x^2-2y^2-x^2+2xy+y^2=x^2+2xy-y^2\)
5: \(\left(3x+4\right)\left(3x-2\right)-\left(3x+1\right)^2\)
\(=9x^2-6x+12x-8-9x^2-6x-1\)
=-9
6: \(4x\left(x-3\right)-\left(2x-1\right)\left(2x+1\right)\)
\(=4x^2-12x-\left(4x^2-1\right)\)
\(=4x^2-12x-4x^2+1=-12x+1\)
7: \(\dfrac{3}{2}x^2-\left(x-1\right)\left(x+1\right)+3x\)
\(=\dfrac{3}{2}x^2+3x-\left(x^2-1\right)\)
\(=\dfrac{3}{2}x^2+3x-x^2+1=\dfrac{1}{2}x^2+3x+1\)
8: \(2\left(5-x\right)\left(5+x\right)-\left(2x+3\right)^2-x\left(3x+2\right)\)
\(=2\left(25-x^2\right)-4x^2-12x-9-3x^2-2x\)
\(=2\left(25-x^2\right)-7x^2-14x-9\)
\(=50-2x^2-7x^2-14x-9=-9x^2-14x+41\)




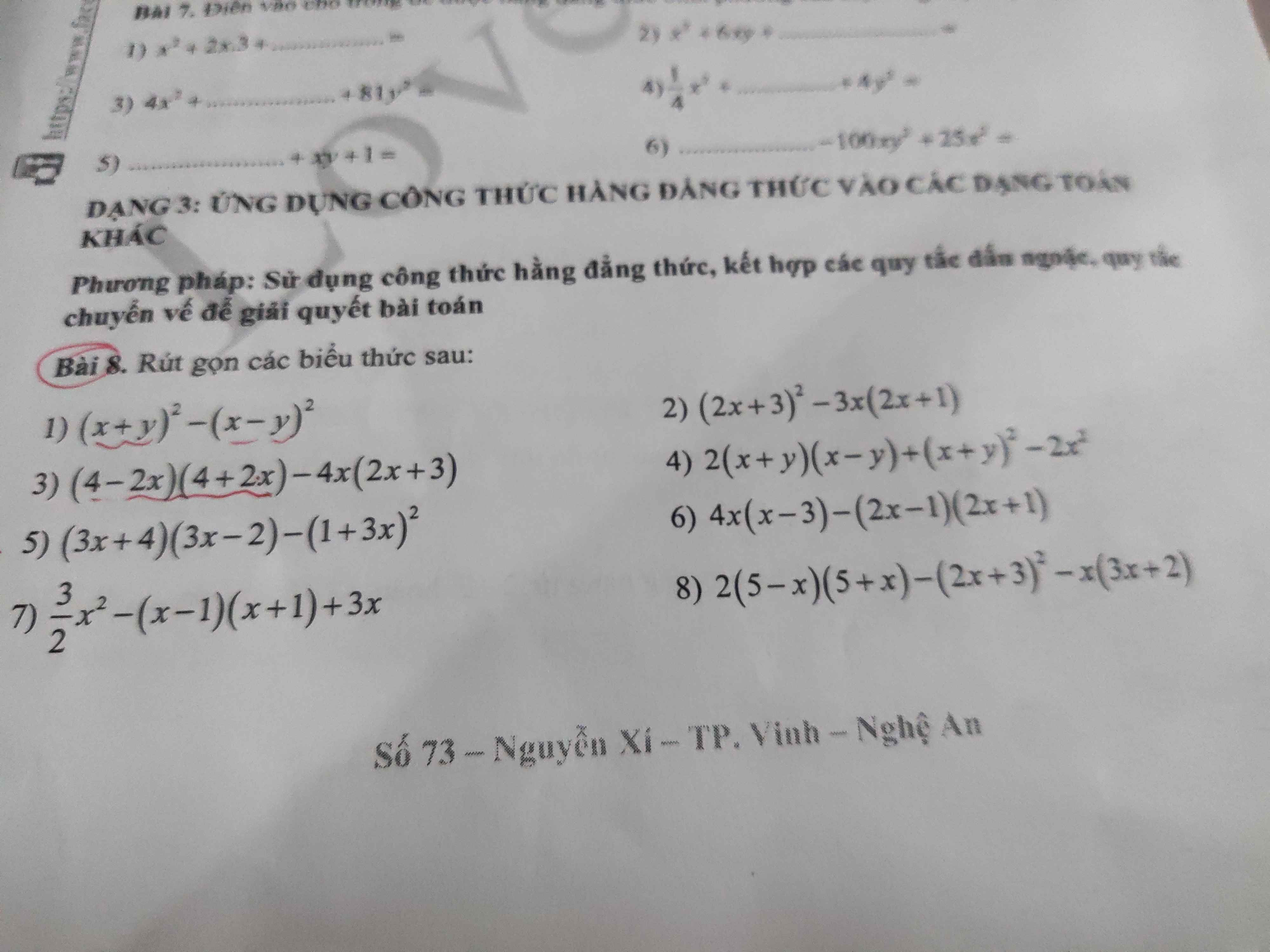
Gọi năng suất dự định của công nhân đó là x(sản phẩm/giờ)
(Điều kiện: \(x\in Z^+\))
Năng suất thực tế là x+2(sản phẩm/giờ)
Thời gian dự kiến hoàn thành là \(\dfrac{15}{x}\left(giờ\right)\)
Thời gian thực tế hoàn thành là \(\dfrac{25}{x+2}\left(giờ\right)\)
Vì người đó hoàn thành đúng thời hạn nên ta có:
\(\dfrac{15}{x}=\dfrac{25}{x+2}\)
=>25x=15(x+2)
=>10x=30
=>x=3(nhận)
vậy: Năng suất dự định là 3 sản phẩm/giờ