Cho hình vuông ABCD. Gọi M, N là trung điểm của BC, CD.
A, Chứng mình rằng AN \(\perp\) DM
B, Gọi H là giao điểm của AN và DM. Biết AB = 2. Tính AH và cos góc MAN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{13}{3}\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{13}{3}=0\left(\text{Đ}KC\text{Đ}:x>0\right)\)
\(\Leftrightarrow\dfrac{3x+3\sqrt{x}+3-13\sqrt{x}}{3\sqrt{x}}=0\)
\(\Rightarrow3x-10\sqrt{x}+3=0\)
Đặt \(\sqrt{x}=t\left(t>0\right)\)
\(\Rightarrow3t^2-10t+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=3\\t=\dfrac{1}{3}\end{matrix}\right.\)( TM)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=\dfrac{1}{9}\end{matrix}\right.\)(TM)
\(ĐK:x>0\\ P=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}=\dfrac{13}{3}< =>3x+3\sqrt{x}+3=13\sqrt{x}\\ < =>3x-10\sqrt{x}+3=0\\ < =>\left(\sqrt{x}-3\right)\left(3\sqrt{x}-1\right)=0\\ =>\left[{}\begin{matrix}\sqrt{x}-3=0\\3\sqrt{x}-1=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=9\\x=\dfrac{1}{9}\end{matrix}\right.\left(TMDK\right)}}\)

\(T=\dfrac{\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}}{\sqrt{\sqrt{5}+1}}-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\dfrac{\sqrt{\left(\sqrt{5}+2\right)\left(\sqrt{5}+1\right)}+\sqrt{\left(\sqrt{5}-2\right)\left(\sqrt{5}+1\right)}}{\sqrt{5}+1}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{7+3\sqrt{5}}+\sqrt{3-\sqrt{5}}}{\sqrt{5}+1}-\sqrt{2}+1\)
\(\sqrt{2}T=\dfrac{\sqrt{14+6\sqrt{5}}+\sqrt{6-2\sqrt{5}}}{\sqrt{5}+1}-2+\sqrt{2}\)
\(=\dfrac{\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}}{\sqrt{5}+1}-2+\sqrt{2}\)
\(=\dfrac{2+2\sqrt{5}}{\sqrt{5}+1}-2+\sqrt{2}=\sqrt{2}\Rightarrow T=\dfrac{\sqrt{2}}{\sqrt{2}}=1\)
\(T=\dfrac{\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}}{\sqrt{\sqrt{5}+1}}-\sqrt{3-2\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{\sqrt{5}+2}+\sqrt{\sqrt{5}-2}\right)^2}}{\sqrt{\sqrt{5}+1}}-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\dfrac{\sqrt{\sqrt{5}+2+2\sqrt{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)+\sqrt{5}-2}}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{2\sqrt{5}+2\sqrt{5-4}}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{2\sqrt{5}+2}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\dfrac{\sqrt{2}.\sqrt{\sqrt{5}+1}}{\sqrt{\sqrt{5}+1}}-\sqrt{2}+1\)
\(=\sqrt{2}-\sqrt{2}+1=1\)

có:
\(\dfrac{1}{2}=0,500000000......\)
theo mk ngĩ số bạn cần tìm là 0 nhé


a) Ta có \(\sqrt{x-4\sqrt{x-4}}=\sqrt{\left(x-4\right)-4\sqrt{x-4}+4}\) \(=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|\)
b) Ta có \(\sqrt{x-2+2\sqrt{x-3}}=\sqrt{\left(x-3\right)+2\sqrt{x-3}+1}\) \(=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\) (vì \(\sqrt{x-3}+1>0\) với \(x\ge3\))
c) Ta có \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\) \(=\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}+\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}\)\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\) \(=\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|\)
d) Ta có \(\sqrt{x-2\sqrt{x}+1}+\sqrt{x+2\sqrt{x}+1}\) \(=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}\) \(=\left|\sqrt{x}-1\right|+\sqrt{x}+1\)

Đặt \(A=2\sqrt{2}+\sqrt{3}\)
Giả sử A là một số hữu tỉ\(\Rightarrow\) A = \(\dfrac{x}{y}\) (tối giản, \(y\ne0\))
\(\Rightarrow2\sqrt{2}+\sqrt{3}=\dfrac{x}{y}\)\(\Rightarrow\left(2\sqrt{2}+\sqrt{3}\right)^2=\dfrac{x^2}{y^2}\Leftrightarrow11+4\sqrt{6}=\dfrac{x^2}{y^2}\)
\(\Leftrightarrow\dfrac{x^2}{y^2}-11=4\sqrt{6}\)
Ta thấy: \(\dfrac{x^2}{y^2};11\) là các số hữu tỉ nên \(\dfrac{x^2}{y^2}-11\) là số hữu tỉ
Mặt khác: \(4\sqrt{6}\) là số vô tỉ
=> \(\dfrac{x^2}{y^2}-11\ne4\sqrt{6}\)
=> Giả sử là sai
=> A là một số vô tỉ
=> \(2\sqrt{2}+\sqrt{3}\) là số vô tỉ

mình chỉ cm đc diều sau:
\(a^2=b^2+c^2-2bc.cosA\) bạn có viết nhầm ko
cách CM:
lần lượt hạ các đường cao AD,BE,CF
ta dễ cm:\(AE.EC+AB.FB=BC^2\) và \(AE.AC=AB.AF\)
\(\Rightarrow AC.EC+AB.BF-AC.AE-AB.AF=BC^2\)
\(\Leftrightarrow b^2+c^2-2AC.AE=a^2\)
\(\Leftrightarrow b^2+c^2-2AC.AB.\dfrac{AE}{AB}=a^2\)
\(\Leftrightarrow a^2=b^2+c^2-2bc.cosA\)(đfcm)

a) \(\sqrt{x-4\sqrt{x-4}}=\sqrt{\left(x-4\right)-4\sqrt{x-4}+4}=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|\)
b) \(\sqrt{x-2+2\sqrt{x-3}}=\sqrt{\left(x-3\right)+2\sqrt{x-3}+1}=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\)
c) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
\(=\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}+\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}\\ =\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\\ =\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|\)
d) \(\sqrt{x-2\sqrt{x}+1}+\sqrt{x+2\sqrt{x}+1}\)
\(=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}\\=\left|\sqrt{x}-1\right|+\sqrt{x}+1\)
a, đk x >= 4
\(\sqrt{x-4-4\sqrt{x-4}+4}=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|=\sqrt{x-4}-2\)
b, đk x >= 3
\(\sqrt{x-3+2\sqrt{x-3}+1}=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\)
c, đk x >= 1
\(\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
\(=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)
d, tương tự

đk x > = 2
\(x^2-3x+2=x-1\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\Leftrightarrow x=1\left(loai\right);x=3\)
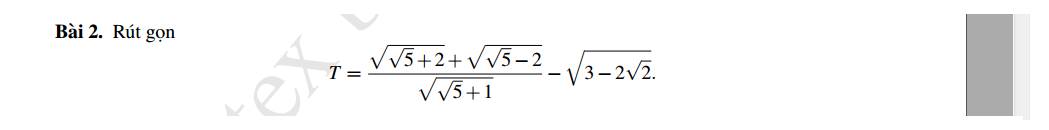
 các bạn giúp mình với
các bạn giúp mình với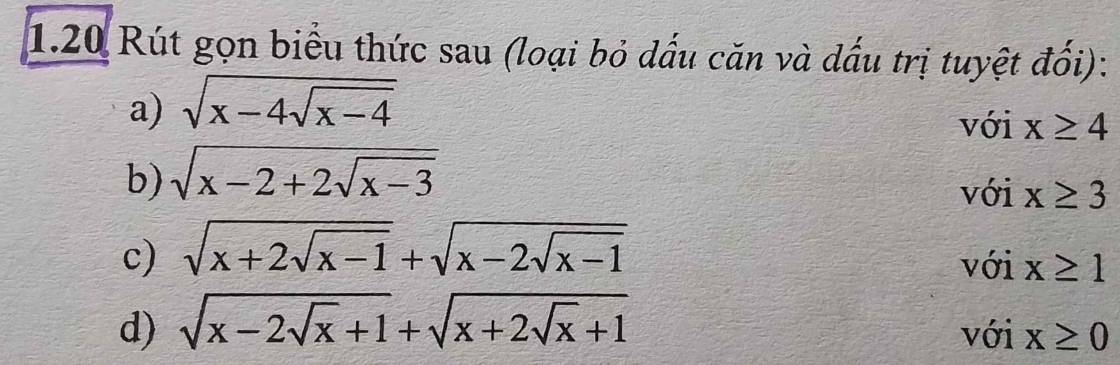
A B C D H M N
Xét tg vuông ADN và tg vuông DCM có
AD=CD (cạnh hình vuông) (1)
Ta có
CD=BC (cạnh hình vuông)
NC=ND; MB=MC (gt)
=> ND=MC=MB=BC/2 (2)
Từ (1) và (2) => tg ADN = tg DCM (Hai tg vuông có 2 cạnh góc vuông bằng nhau) \(\Rightarrow\widehat{DAN}=\widehat{CDM}\)
Mà \(\widehat{CDM}+\widehat{ADM}=\widehat{ADC}=90^o\)
\(\Rightarrow\widehat{DAN}+\widehat{ADM}=90^o\)
Xét tg ADH có
\(\widehat{DAN}+\widehat{ADM}=90^o\Rightarrow\widehat{AHD}=90^o\Rightarrow AN\perp DM\)
b/
Xét tg vuông ADN có
\(DN=\dfrac{CD}{2}=\dfrac{AB}{2}=\dfrac{2}{2}=1\)
\(AN=\sqrt{AD^2+DN^2}=\sqrt{2^2+1^2}=\sqrt{5}\) (Pitago)
\(DN^2=NH.AN\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow NH=\dfrac{DN^2}{AN}=\dfrac{1^2}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)
\(\Rightarrow AH=AN-NH=\sqrt{5}-\dfrac{\sqrt{5}}{5}=\dfrac{4\sqrt{5}}{5}\)
Xét tg vuông ADN và tg vuông ABM có
AD=AB (cạnh hình vuông)
ND=MB (cmt)
=> tg ADN = tg ABM (Hai tg vuông có 2 cạnh góc vuông bằng nhau)
\(\Rightarrow\widehat{DAN}=\widehat{BAM}=\alpha\)
Ta có \(\widehat{MAN}=\widehat{BAD}-\widehat{DAN}-\widehat{BAM}=\dfrac{\Pi}{2}-2\alpha\)
\(\Rightarrow\cos\widehat{MAN}=\cos\left(\dfrac{\Pi}{2}-2\alpha\right)=\sin2\alpha=2\sin\alpha.\cos\alpha\)
Mà
\(\sin\alpha=\dfrac{DN}{AN}=\dfrac{1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5};\cos\alpha=\dfrac{AD}{AN}=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(\Rightarrow\cos\widehat{MAN}=2.\dfrac{\sqrt{5}}{5}.\dfrac{2\sqrt{5}}{5}=\dfrac{4}{5}=0,8\)