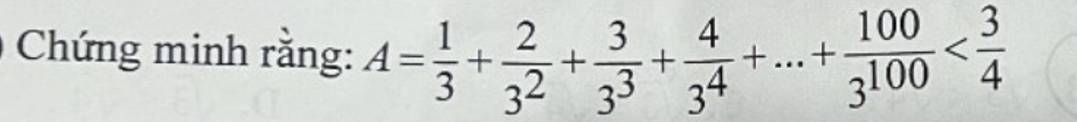
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giá bán của một chiếc iphone ban đầu là:
25 000 000 x 160 : 100 = 40 000 000 (đồng)
Số tiền lần đầu thu được khi bán 90 chiếc iphone là
40 000 000 x 90 = 3 600 000 000 (đồng)
Số iphone còn lại sau đợt bán thứ nhất là:
120 - 90 = 30 (chiếc)
Giá của mỗi chiếc iphone còn lại là:
40 000 000 x (100% - 50%) = 20 000 000 (đồng)
Số tiền thu được khi bán 30 chiếc iphone còn lại là:
20 000 000 x 30 = 600 000 000 (đồng)
Tổng số tiền điện máy xanh thu được khi bán hết 120 chiếc iphone là:
3 600 000 000 + 600 000 000 = 4 200 000 000 (đồng)
Giá vốn của 120 chiếc iphone là:
25 000 000 x 120 = 3 000 000 000 (đồng)
Sau khi bán hết 120 chiếc iphone điện máy xanh lãi và lãi số tiền là:
4 200 000 000 - 3 000 000 000 = 1 200 000 000 (đồng)
Đáp số:...
Giá bán của một chiếc iphone ban đầu là:
25 000 000 x 160 : 100 = 40 000 000 (đồng)
Số tiền lần đầu thu được khi bán 90 chiếc iphone là
40 000 000 x 90 = 3 600 000 000 (đồng)
Số iphone còn lại sau đợt bán thứ nhất là:
120 - 90 = 30 (chiếc)
Giá của mỗi chiếc iphone còn lại là:
40 000 000 x (100% - 50%) = 20 000 000 (đồng)
Số tiền thu được khi bán 30 chiếc iphone còn lại là:
20 000 000 x 30 = 600 000 000 (đồng)
Tổng số tiền điện máy xanh thu được khi bán hết 120 chiếc iphone là:
3 600 000 000 + 600 000 000 = 4 200 000 000 (đồng)
Giá vốn của 120 chiếc iphone là:
25 000 000 x 120 = 3 000 000 000 (đồng)
Sau khi bán hết 120 chiếc iphone điện máy xanh lãi và lãi số tiền là:
4 200 000 000 - 3 000 000 000 = 1 200 000 000 (đồng)
Đáp số:...

A = \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + \(\dfrac{1}{4}\) +...+ \(\dfrac{1}{2007}\) + \(\dfrac{1}{2008}\) + \(\dfrac{1}{2009}\)
B = 2008 + \(\dfrac{2007}{2}\) + \(\dfrac{2006}{3}\)+ ... + \(\dfrac{2}{2007}\) + \(\dfrac{1}{2008}\)
B = (1 + \(\dfrac{2007}{2}\)) + (1 + \(\dfrac{2006}{3}\)) + .. + (1 + \(\dfrac{2}{2007}\)) + (1 + \(\dfrac{1}{2008}\)) + 1
B = \(\dfrac{2+2007}{2}\) + \(\dfrac{3+2006}{3}\) +... + \(\dfrac{2007+2}{2007}\) + \(\dfrac{2008+1}{2008}\) + \(\dfrac{2009}{2009}\)
B = \(\dfrac{2009}{2}\) + \(\dfrac{2009}{3}\) + ... + \(\dfrac{2009}{2007}\) + \(\dfrac{2009}{2008}\) + \(\dfrac{2009}{2009}\)
B = 2009.( \(\dfrac{1}{2}\) + \(\dfrac{1}{3}\) + ....+ \(\dfrac{1}{2007}\) + \(\dfrac{1}{2008}\) + \(\dfrac{1}{2009}\))
Tỉ số của \(\dfrac{A}{B}\)
\(\dfrac{A}{B}\)= \(\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}}{2009.\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}\right)}\)
\(\dfrac{A}{B}\) = \(\dfrac{1}{2009}\)

\(x^2=3+5+2\sqrt{15}=8+\sqrt{60}\)
\(y^2=2+6+2\sqrt{12}=8+\sqrt{48}\)
Mà \(60>48\Rightarrow\sqrt{60}>\sqrt{48}\Rightarrow8+\sqrt{10}>8+\sqrt{48}\)
\(\Rightarrow x^2>y^2\Rightarrow x>y\) (do x;y đều dương)

(2y-1)¹⁰=(2y-1)²⁰
→ (2y-1)²⁰-(2y-1)¹⁰=0
→ (2y-1)¹⁰.[(2y-1)¹⁰-1]=0
→ (2y-1)¹⁰=0 hay (2y-1)¹⁰-1=0
→ 2y-1=0 hay 2y-1=1 hay 2y-1=-1
→ y=½ hay y=1 hay y=0

Lãi suất:
214 400 000 : 200 000 000 x 100% - 100% = 7,2%
Đáp số:.......

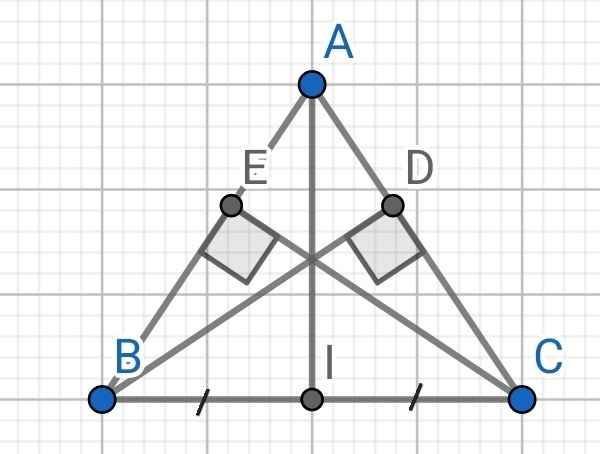 a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC

\(A=\dfrac{1}{3}+\dfrac{2}{3^2}+\dfrac{3}{3^3}+...+\dfrac{100}{3^{100}}\)
\(3A=1+\dfrac{2}{3}+\dfrac{3}{3^2}+...+\dfrac{100}{3^{99}}\)
\(\Rightarrow3A-A=1+\dfrac{2}{3}-\dfrac{1}{3}+\dfrac{3}{3^2}-\dfrac{2}{3^2}+\dfrac{4}{3^3}-\dfrac{3}{3^3}+...+\dfrac{100}{3^{99}}-\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow2A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{100}{3^{100}}\)
\(\Rightarrow6A=3+1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}-\dfrac{100}{3^{99}}\)
\(\Rightarrow6A-2A=3-\dfrac{101}{3^{99}}+\dfrac{100}{3^{100}}\)
\(\Rightarrow4A=3-\dfrac{203}{3^{100}}< 3\)
\(\Rightarrow A< \dfrac{3}{4}\)
\(A< \dfrac{3}{4}\)