cho x + y + xy = 8. Tìm GTNN của P = x2 + y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$(\sqrt{2}x+\sqrt{8}y)^2=(\sqrt{2}x)^2+(\sqrt{8}y)^2+2\sqrt{2}x.\sqrt{8}y$
$=2x^2+8y^2+8xy$

Lời giải:
Gọi biểu thức trên là $A$
$4A=4a^2+4ab+4b^2-12a-12b+8064$
$=(4a^2+4ab+b^2)+3b^2-12a-12b+8064$
$=(2a+b)^2-6(2a+b)+(3b^2-6b)+8064$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)+8052$
$=(2a+b-3)^2+3(b-1)^2+8052\geq 8052$
$\Rightarrow A\geq 2013$
Vậy $A_{\min}=2013$

\(a,\left(x-1\right)\left(x-2\right)>\left(x-1\right)^2\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(x-1\right)^2>0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x-2\right)-\left(x-1\right)\right]>0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2-x+1\right)>0\)
\(\Leftrightarrow\left(x-1\right)\left(-1\right)>0\)
\(\Leftrightarrow x-1< 0\)
\(\Leftrightarrow x< 1\)
Vậy \(S=\left\{x|x< 1\right\}\)
\(b,\left(4x-1\right)\left(x^2+1\right)\left(-x+4\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-1>0\\x^2+1>0\forall x\left(x^2\ge0\forall x\right)\\-x+4>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{1}{4}\\x< 4\end{matrix}\right.\)
Vậy \(S=\left\{x|\dfrac{1}{4}< x< 4\right\}\)

a)
`(2x-3)(x+4)>2(x^2 +1)`
`<=>2x^2 +8x-3x-12>2x^2 +2`
`<=>5x>14`
`<=>x>14/5`
//////////////////////l/////////////l---------->
`0` `14/5`
b)
`(3x-1)/2-(5x+1)/3>4`
`<=>(9x-3)/6-(10x+2)/6>24/6`
`<=>9x-3-10x-2>24`
`<=>-x>29`
`<=>x<-29`
-------------l////////////////l////////////////////
-29 0


`@` `\text {Ans}`
`\downarrow`
`x(1-x) + (x-1)^2`
`= x-x^2 + x^2 - 2x + 1`
`= (x-2x) + (-x^2 + x^2) + 1`
`= -x+1`
x ( 1 - x ) + ( x - 1 )2 = x - x2 + x2 - 2x + 1 = -x + 1 = 1 - x
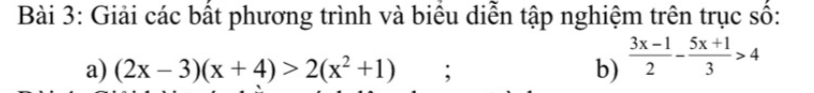

Lời giải:
Áp dụng BĐT AM-GM:
$x^2+2^2\geq 4x$
$y^2+2^2\geq 4y$
$2(x^2+y^2)\geq 4xy$
$\Rightarrow 3(x^2+y^2)+8\geq 4(x+y+xy)=32$
$\Rightarrow x^2+y^2\geq 8$
Vậy $P_{\min}=8$ khi $x=y=2$