cho tam giác ABC vuông tại A , đường cao AH , biết AB = 5cm , BC=13cm. Tính AH , BH , CH , AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ĐK: \(x^2-4x+4\ge0\Leftrightarrow\left(x-2\right)^2\ge0\) (luôn đúng)
\(\sqrt{x^2-4x+4}=x+2\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=x+2\\ \Leftrightarrow\left|x-2\right|=x+2\)
TH1: \(x-2\ge0\Leftrightarrow x\ge2\)
PT trở thành: \(x-2=x+2\Leftrightarrow-2=2\) (vô lí)
TH2: \(x-2< 0\Leftrightarrow x< 2\)
PT trở thành: \(2-x=x+2\Leftrightarrow2x=0\Leftrightarrow x=0\) (TM)
Vậy PT có nghiệm \(x=0\)
\(\sqrt{x^2-4x+4}=x+2\) \(ĐK: x \ge -2\)
\(<=>\sqrt{(x-2)^2}=x+2\)
`<=>|x-2|=x+2`
`@` Với `x-2 >= 0<=>x >= 2=>|x-2|=x-2` ptr có dạng:
`x-2=x+2`
`<=>0x=4` (Vô lí)
`@` Với `x-2 < 0<=>x < 2` Kết hợp đk \(=>-2 \le x < 2=>|x-2|=2-x` ptr có dạng:
`2-x=x+2`
`<=>2x=0`
`<=>x=0` (t/m)
Vậy `S=`{`0`}

Bài 6 ;mk ko chép lại đề bài nữa nhé
1, p=[1-\(\dfrac{4}{\sqrt{x}+1}+\dfrac{1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)]:\(\dfrac{x-2\sqrt{x}}{x-1}\)
=\(\left[\dfrac{x-1-4\left(\sqrt{x}-1\right)+1}{x-1}\right]:\dfrac{x-2\sqrt{x}}{x-1}\)
=\(\left[\dfrac{x-1-4\sqrt{x}+4+1}{x-1}\right]:\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-1}\)
=\(\dfrac{\left(\sqrt{x}-2\right)^2}{x-1}\times\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
=\(\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
b, p=\(\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{x}=4\)
\(\Leftrightarrow x=16\)



Có AH là đường cao của Δ ABC (gt)
=> AH ⊥ BC tại H
=> Δ ABH vuông tại H
=> \(AB^2=AH^2+BH^2\) (py-ta-go)
=> BH² = AB² – AH² = 36 – (4,8)² = 12,96
=> BH = 3,6 cm
áp dụng hệ thức lượng trong Δ ABC ta có
AB² = BH.BC
=> \(BC=\dfrac{AB^2}{BH}=\dfrac{36}{3,6}=10cm\)
khi đó diện tích \(\Delta ABC=\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.4,8.10=24cm^2\)
Cách 2:
Áp dụng hệ thức lượng trong Δ ABC ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay \(AH^2=\dfrac{AB^2.AC^2}{AB^2+AC^2}\)
=>\(\left(4,8\right)^2=\dfrac{36.AC^2}{36+AC^2}\)
=> AC =8 cm
Khi đó diện tích\(\Delta ABC=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.6.8=24cm^2\)

a) Xét (O) có \(\widehat{DBC}\) và \(\widehat{DAB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn \(\stackrel\frown{BC}\) nên ta có \(\widehat{DBC}=\widehat{DAB}\). Từ đó, ta dễ dàng chứng minh \(\Delta DBC~\Delta DAB\left(g.g\right)\) \(\Rightarrow\dfrac{DC}{DB}=\dfrac{DB}{DA}\) \(\Rightarrow BD^2=AD.CD\) (đpcm)
b) Gọi I là giao điểm của BD và CE.
Xét (O) có 2 tiếp tuyến tại B và C cắt nhau tại I nên \(IB=IC\), dẫn đến tam giác IBC cân tại I, từ đó \(\widehat{IBC}=\widehat{ICB}\) (1)
Tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\) \(\Rightarrow180^o-\widehat{ABC}=180^o-\widehat{ACB}\) \(\Rightarrow\widehat{EBC}=\widehat{DCB}\) (2)
Từ (1) và (2), ta có \(\widehat{EBC}-\widehat{IBC}=\widehat{DCB}-\widehat{ICB}\) \(\Rightarrow\widehat{DBE}=\widehat{DCE}\)
Từ đó dễ dàng chứng minh tứ giác BCDE nội tiếp.
c) Tứ giác BCDE nội tiếp nên \(\widehat{EBC}+\widehat{CDE}=180^o\)
Mà \(\widehat{EBC}=\widehat{DCB}\) nên \(\widehat{DCB}+\widehat{CDE}=180^o\) \(\Rightarrow BC//DE\) (2 góc trong cùng phía bù nhau)
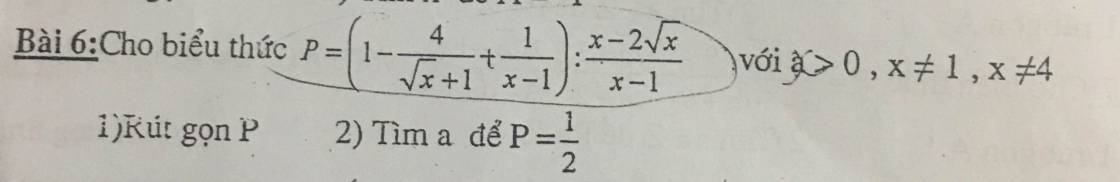
Áp dụng định lí pytago trong tam giác vuông ABC tại A , ta có :
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow5^2+AC^2=13^2\)
\(\Leftrightarrow AC^2=13^2-5^2\)
\(\Leftrightarrow AC=\sqrt{144}=12\left(cm\right)\)
+) Xét tam giác ABC vuông tại A , đường cao AH:
\(\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\\AH^2=CH.BH\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5^2=BH.13\\12^2=CH.13\\AH^2=BH.CH\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{25}{13}\\CH=\dfrac{144}{13}\\AH=\sqrt{\dfrac{25}{13}.\dfrac{144}{13}}=\dfrac{60}{13}\end{matrix}\right.\)