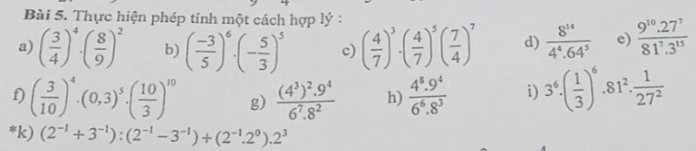trên 1 đường thẳng AB,1 người đi xe đạp từ A đến B với tốc độ không đổi v=15km/h hết thời gian t.nếu người ấy tăng tốc độ thêm 3 km/h thì đi từ A đến B sớm hơn 15 phút.tìm quãng đường AB và thời gian t.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 6
a; (\(\dfrac{3}{4}\))4.(\(\dfrac{8}{9}\))2
= (\(\dfrac{3}{2^2}\))4.(\(\dfrac{2^3}{3^2}\))2
= \(\dfrac{3^4}{2^8}\).\(\dfrac{2^6}{3^4}\)
= \(\dfrac{3^4.2^6}{3^4.2^6}\). \(\dfrac{1}{2^2}\)
= \(\dfrac{1}{2^2}\)
= \(\dfrac{1}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 6
b; (\(\dfrac{-3}{5}\))6.(-\(\dfrac{5}{3}\))5
= \(\dfrac{3^6}{5^6}\).\(\dfrac{\left(-5\right)^5}{3^5}\)
= \(\dfrac{-5^5.3^5}{5^5.3^5}\).\(\dfrac{3}{5}\)
= - 1.\(\dfrac{3}{5}\)
= - \(\dfrac{3}{5}\)
S
20 tháng 6
số km mà an đi đã dừng lại ở 1/4 quãng đường là: \(\dfrac{1}{4}\cdot6=1,5\left(km\right)\)
tổng quãng đường an đi là: 1,5 + 1,5 + 6 = 9 (km)
gọi thời gian dự kiến đến trường là t (giờ)
vì an đi đến trường trễ 15p nên: t + 0,25 (giờ)
vì tốc độ dự kiến của an là: \(v=\dfrac{6}{t}\)
tốc độ thực tế của an là: \(v=\dfrac{9}{t+0,25}\)
mà tốc độ dự kiến và tốc độ thực tế không đổi nên ta có:
\(\dfrac{6}{t}=\dfrac{9}{t+0,25}\\ 6\cdot\left(t+0,25\right)=9t\\ 6t+1,5=9t\\ 1,5=3t\\ t=0,5\)
vậy tốc độ đi của an là: \(\dfrac{6}{0,5}=12\left(km\text{⁄}h\right)\)
thời gian thực tế ân đi là: t + 0,25 = 0,5 + 0,25 = 0,75 (giờ) = 45p
thời gian mà an đi đến trường là: 6h00p + 0h45p = 6h45p
giờ vào lớp của an là: 6h45p - 0h15p = 6h30p
vậy a) tốc độ của an 12km/h
b) thời gian vào lớp 6h30p
