Khảo sát và vẽ đồ thị hàm số $y=\dfrac{x^2-x-1}{x-2}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

a) \(y=\dfrac{x+1}{x-2}\)
\(y'=-\dfrac{3}{\left(x-2\right)^2}< 0\forall x\inℝ\ \left\{2\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
b) \(y=\dfrac{2x+1}{x-1}\)
\(y'=-\dfrac{3}{\left(x-1\right)^2}< 0\forall x\inℝ\ \left\{1\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;1\right)\) và \((1;+\infty)\)


64.
d qua \(M\left(-3;1;2\right)\) và có vtcp \(\left(2;4;-1\right)\) nên có pt:
\(\left\{{}\begin{matrix}x=-3+2t\\y=1+4t\\z=2-t\end{matrix}\right.\)
C đúng
65.
\(\overrightarrow{AB}=\left(1;0;2\right)\) nên C đúng
66.
d qua \(M\left(3;-2;-6\right)\)
67.
mp vuông góc d nên nhận \(\left(1;2;-2\right)\) là 1 vtpt
Phương trình:
\(1\left(x-3\right)+2\left(y+2\right)-2\left(z-2\right)=0\)
\(\Leftrightarrow x+2y-2z+5=0\)
68.
M là giao d và (P) nên tọa độ thỏa mãn:
\(\left(-3+2t\right)+2\left(-1+t\right)-\left(3+t\right)+5=0\)
\(\Rightarrow t=1\)
Thay vào pt d:
\(\Rightarrow M\left(-1;0;4\right)\)
69.
\(\overrightarrow{BC}=\left(1;2;-1\right)\)
Đường thẳng đi qua A và song song BC nhận (1;2;-1) là 1 vtcp nên có pt:
\(\dfrac{x-1}{1}=\dfrac{y-2}{2}=\dfrac{z}{-1}\)

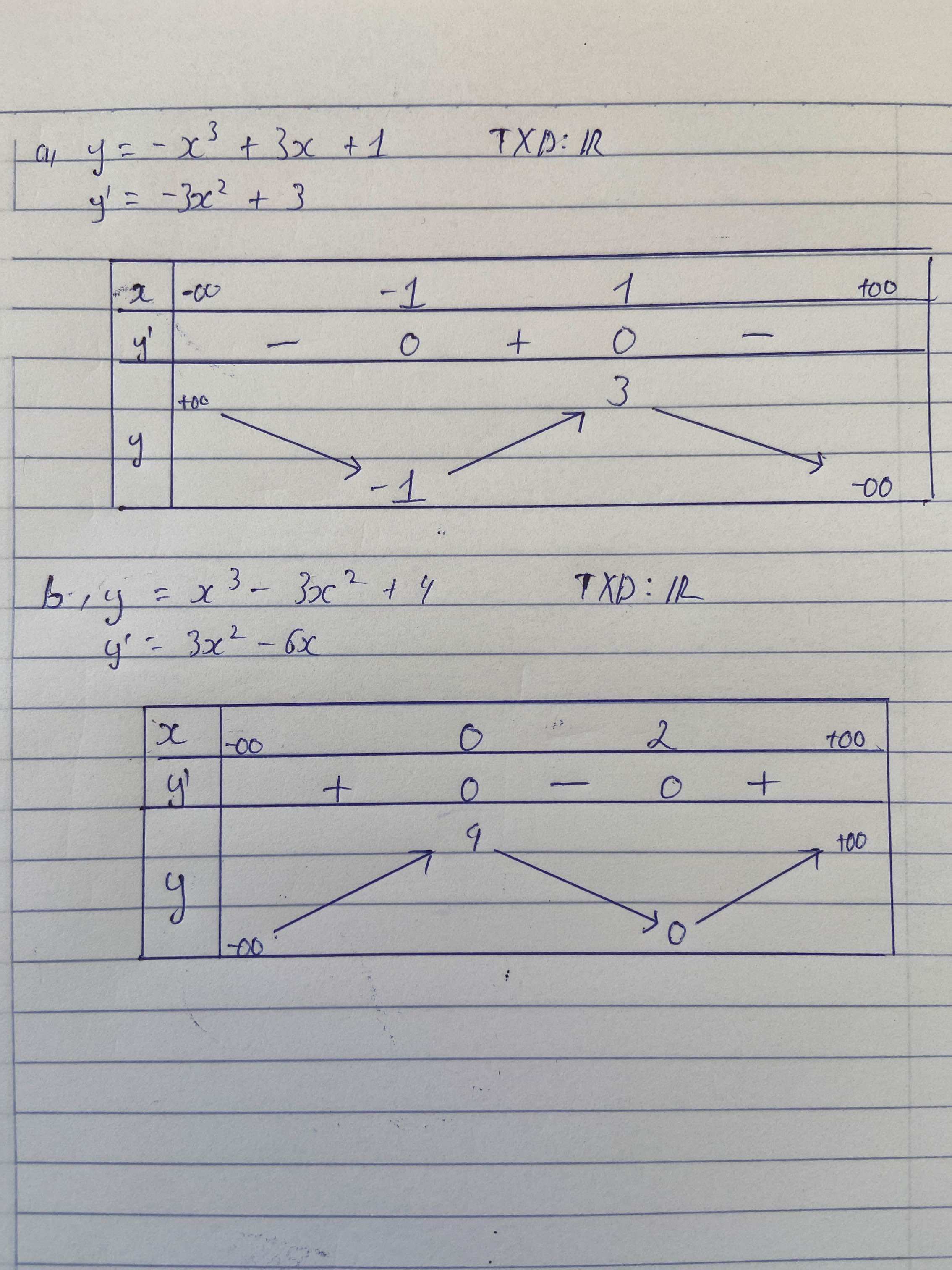
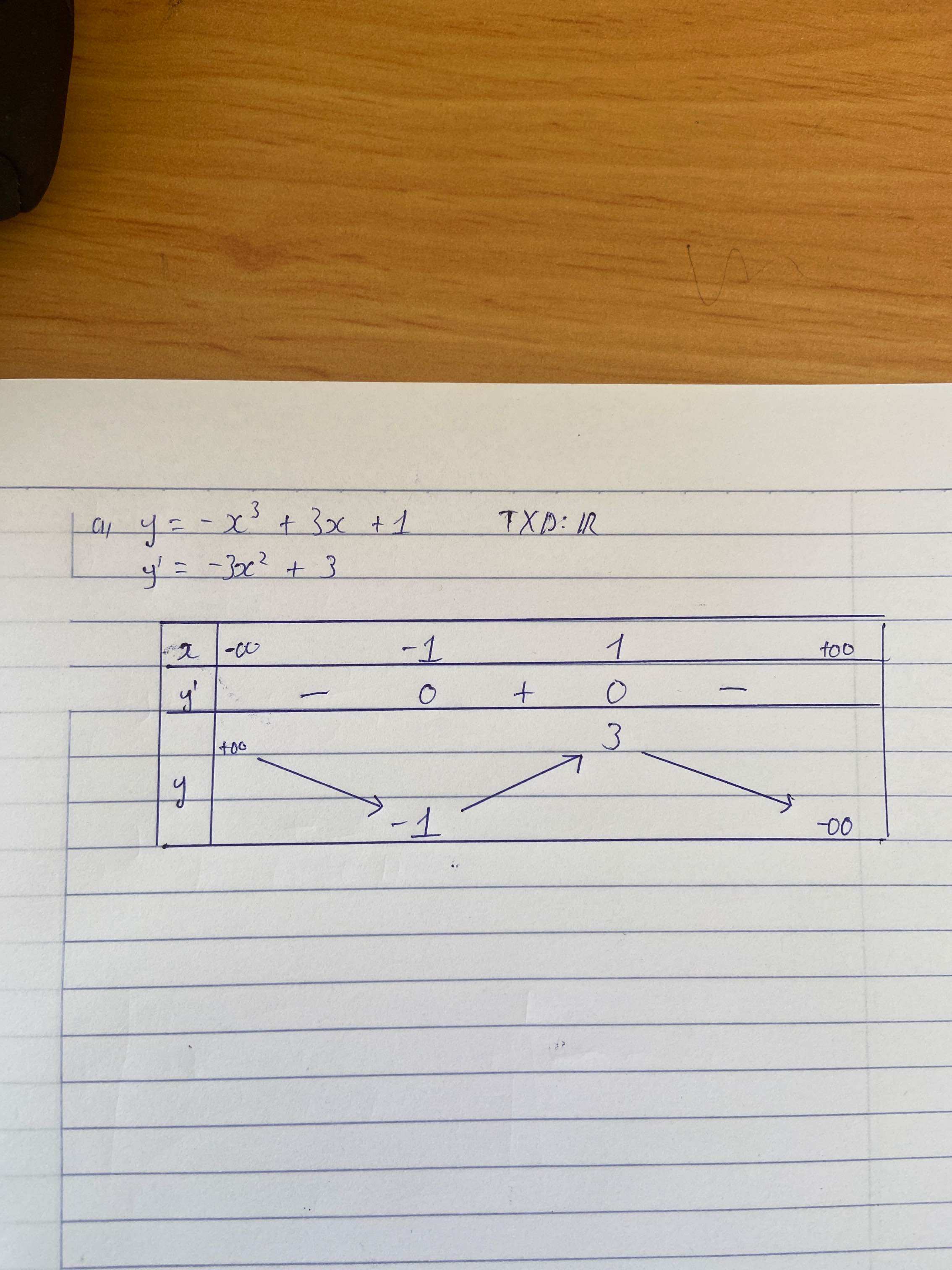
Trên \(\left[0;3\right]\) hàm \(y=x^2-3x\) âm nên ta cần "xoay" nó lên thành \(y=3x-x^2\)
Khi đó:
Pt hoành độ giao điểm trên \(\left[0;3\right]\): \(3x-x^2=x\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Pt hoành độ giao điểm với \(x>3\): \(x^2-3x=x\Rightarrow x=4\)
Do đó:
\(V=\pi\int\limits^2_0\left(3x-x^2\right)^2dx+\pi\int\limits^4_2x^2dx-\pi\int\limits^4_3\left(x^2-3x\right)^2dx=\dfrac{611\pi}{30}\)
\(\Rightarrow18a-300b=1998\)


\(\overrightarrow{BA}=\left(1;1;2\right)\)
Pt AB có dạng: \(\left\{{}\begin{matrix}x=-2+t\\y=1+t\\z=1+2t\end{matrix}\right.\)
Pt mặt phẳng qua C và vuông góc AB có dạng:
\(1\left(x-5\right)+y+2z=0\)
\(\Leftrightarrow x+y+2z-5=0\)
Tọa độ H thỏa mãn:
\(\left(-2+t\right)+\left(1+t\right)+2\left(1+2t\right)-5=0\)
\(\Rightarrow t=\dfrac{2}{3}\Rightarrow H\left(-\dfrac{4}{3};\dfrac{5}{3};\dfrac{7}{3}\right)\)
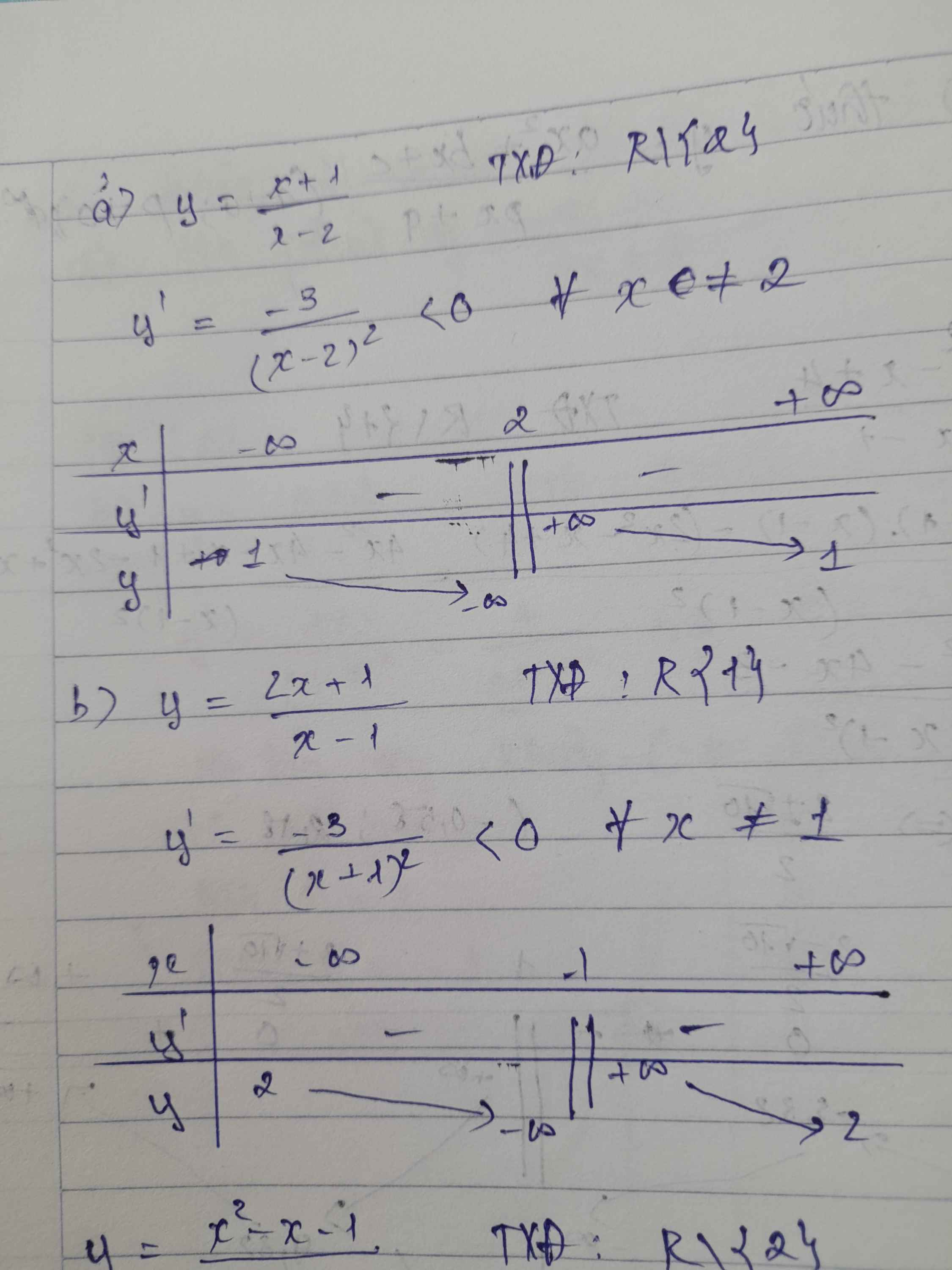






Tập xác định \(D=ℝ\backslash\left\{2\right\}\)
TCĐ: \(x=2\)
Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)
nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)
Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
BBT