a: ΔABC đều

mà AI là đường trung tuyến

nên AI\(\perp\)BC

ta có: BC\(\perp\)AI

BC\(\perp\)SA(SA\(\perp\)(ABC))

SA,AI cùng thuộc mp(SAI)

Do đó: BC\(\perp\)(SAI)

b: Vì ΔABC đều nên \(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)

\(V_{S.ABCD}=\dfrac{1}{3}\cdot SA\cdot S_{ABC}=\dfrac{1}{3}\cdot\dfrac{a^2\sqrt{3}}{4}\cdot2a=\dfrac{a^3\sqrt{3}}{6}\)

a: Ta có: BD\(\perp\)AC(ABCD là hình vuông)

BD\(\perp\)SA(SA\(\perp\)(ABCD))

SA,AC cùng thuộc mp(SAC)

Do đó: BD\(\perp\)(SAC)

b: BC\(\perp\)AB(ABCD là hình vuông)

BC\(\perp\)SA(SA\(\perp\)(ABCD))

SA,AB cùng thuộc mp(SAB)

Do đó: BC\(\perp\)(SAB)

c: DC\(\perp\)AD(ABCD là hình vuông)

DC\(\perp\)SA(SA\(\perp\)(ABCD))

AD,SA cùng thuộc mp(SAD)

Do đó: DC\(\perp\)(SAD)

Gọi số tháng tối thiểu để ông An có tổng cộng là 600 triệu đồng là x(tháng)

(ĐK: x>0)

Sau 1 tháng, số tiền ông An có được là \(500\cdot\left(1+0,7\%\right)\left(triệuđồng\right)\)

=>Sau x tháng, số tiền ông An có được là:

\(500\left(1+0,7\%\right)^x\left(triệuđồng\right)\)

Theo đề, ta có:

\(500\left(1+0,7\%\right)^x=600\)

=>\(\left(1+0,7\%\right)^x=1,2\)

=>\(x=log_{1+0,7\%}1,2\simeq26\)

Vậy: ông An cần gửi ít nhất 26 tháng

12 tháng

\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}\dfrac{x^2-5x+6}{x-3}\)

\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-2\right)\left(x-3\right)}{x-3}=\lim\limits_{x\rightarrow3}x-2=3-2=1\)

\(f\left(3\right)=5m+11\)

Để hàm số liên tục tại x=3 thì 5m+11=1

=>5m=-10

=>m=-2

\(P=m^2-4=\left(-2\right)^2-4=0\)

我需要你的帮助

ĐKXĐ: \(\left[{}\begin{matrix}x\ge2\\x\le0\end{matrix}\right.\)

\(f'\left(x\right)=\dfrac{x-1}{\sqrt{x^2-2x}}\)

\(f'\left(x\right)\ge f\left(x\right)\Leftrightarrow\dfrac{x-1}{\sqrt{x^2-2x}}\ge\sqrt{x^2-2x}\)

\(\Rightarrow x-1\ge x^2-2x\)

\(\Rightarrow x^2-3x+1\le0\)

\(\Rightarrow\dfrac{3-\sqrt{5}}{2}\le x\le\dfrac{3+\sqrt{5}}{2}\)

Kết hợp ĐKXĐ \(\Rightarrow2\le x\le\dfrac{3+\sqrt{5}}{2}\)

\(\Rightarrow x=2\) là giá trị nguyên duy nhất thỏa mãn

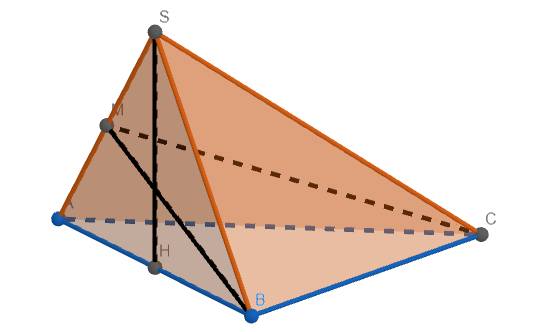
a) Gọi M là trung điểm SA. 

Có \(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\).

Lại có \(BC\perp BA\) \(\Rightarrow BC\perp\left(SAB\right)\) \(\Rightarrow BC\perp SB\)

Do đó \(\widehat{\left(ABC\right),\left(SBC\right)}=\widehat{SBA}=60^o\)

Khi đó tam giác ABC đều \(\Rightarrow AB=BC=SB=SA=4\)

Đồng thời \(MB\perp SA\)

Mặt khác, ta thấy \(\Delta ABC=\Delta SBC\left(c.g.c\right)\) \(\Rightarrow SC=AC\)

\(\Rightarrow\Delta SAC\) cân tại C \(\Rightarrow MC\perp SA\)

Do đó \(\widehat{\left(SAC\right),\left(SAB\right)}=\widehat{BMC}\)

Vì \(BC\perp\left(SAB\right)\Rightarrow BC\perp BM\Rightarrow\Delta BCM\) vuông tại B

\(\Rightarrow\cos\widehat{BMC}=\dfrac{BC}{CM}=\dfrac{4}{\dfrac{4\sqrt{3}}{2}}=\dfrac{2\sqrt{3}}{3}\) 

Vậy \(\cos\widehat{\left(SAC\right),\left(SAB\right)}=\dfrac{2\sqrt{3}}{3}\)

Mình gửi trả lời rồi đó, bạn vào trang cá nhân của mình xem nhé.

 Bạn viết lại đề bài nhé, chứ nhìn vào mình không biết nó là \(\left(\dfrac{1}{3}\right)^{x^2}-2x-3=3^x+1\) hay \(\left(\dfrac{1}{3}\right)^{x^2-2x-3}=3^{x+1}\) hay cái gì khác nữa.

\(\left(\dfrac{1}{3}\right)^{x^2-2x-3}=3^{x+1}\)

=>\(3^{-x^2+2x+3}=3^{x+1}\)

=>\(-x^2+2x+3=x+1\)

=>\(-x^2+x+2=0\)

=>\(x^2-x-2=0\)

=>(x-2)(x+1)=0

=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

log₂(x - 1) = 3

⇒ x - 1 = 2³

x - 1 = 8

x = 8 + 1

x = 9

cảm ơn bạn linh nha