Giải phương trình:
\(x^4+2x^3-x^2-2x+1=0\)
Giúp với tui nghĩ mãi ko ra
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(x + 2y)² - (x - y)²
= (x + 2y - x + y)(x + 2y + x - y)
= 3y(2x + y)
\(\left(x+2y\right)^2-\left(x-y\right)^2\)
\(=\left[\left(x+2y\right)-\left(x-y\right)\right]\left[\left(x+2y\right)+\left(x-y\right)\right]\)
\(=\left(x+2y-x+y\right)\left(x+2y+x-y\right)\)
\(=3y\left(2x+y\right)\)

Bài 2
a) 3x(x - 1) - 3(x - 1) = 0
(x - 1)(3x - 3) = 0
3(x - 1)(x - 1) = 0
3(x - 1)² = 0
x - 1 = 0
x = 1
b) x² - x = 0
x(x - 1) = 0
x = 0 hoặc x - 1 = 0
*) x - 1 = 0
x = 1
Vậy x = 0; x = 1
c) 25x² - 100x = 0
25x(x - 4) = 0
25x = 0 hoặc x - 4 = 0
*) 25x = 0
x = 0
*) x - 4 = 0
x = 4
Vậy x = 0; x = 4
d) (2x - 1)² - 64 = 0
(2x - 1 - 8)(2x - 1 + 8) = 0
(2x - 9)(2x + 7) = 0
*) 2x - 9 = 0
2x = 9
x = 9/2
*) 2x + 7 = 0
2x = -7
x = -7/2
Vậy x = -7/2; x = 9/2

Bài 4
1) x⁴ - 9x³ + x² - 9x
= x(x³ - 9x² + x - 9)
= x[(x³ - 9x²) + (x - 9)]
= x[x²(x - 9) + (x - 9)]
= x(x - 9)(x² + 1)
2) 3x² + 5y - 3xy - 5x
= (3x² - 3xy) - (5x - 5y)
= 3x(x - y) - 5(x - y)
= (x - y)(3x - 5)
3) xy + z + y + xz
= (xy + xz) + (y + z)
= x(y + z) + (y + z)
= (y + z)(x + 1)
4) x² + y - xy - x
= (x² - xy) - (x - y)
= x(x - y) - (x - y)
= (x - y)(x - 1)
Bài 5
1) x² + 2x - 8
= x² - 2x + 4x - 8
= (x² - 2x) + (4x - 8)
= x(x - 2) + 4(x - 2)
= (x - 2)(x + 4)
2) x² + 5x + 6
= x² + 2x + 3x + 6
= (x² + 2x) + (3x + 6)
= x(x + 2) + 3(x + 2)
= (x + 2)(x + 3)
3) 4x² - 12x + 8
= 4(x² - 3x + 2)
= 4(x² - x - 2x + 2)
= 4[(x² - x) - (2x - 2)]
= 4[x(x - 1) - 2(x - 1)]
= 4(x - 1)(x - 2)
4) x² + 6x + 8
= x² + 2x + 4x + 8
= (x² + 2x) + (4x + 8)
= x(x + 2) + 4(x + 2)
= (x + 2)(x + 4)
5) x² + 10x + 16
= x² + 2x + 8x + 16
= (x² + 2x) + (8x + 16)
= x(x + 2) + 8(x + 2)
= (x + 2)(x + 8)
6) (x + 1)² - 4
= (x + 1 - 2)(x + 1 + 2)
= (x - 1)(x + 3)
7) 9 - 6x + x² - y²
= (9 - 6x + x²) - y²
= (3 - x)² - y²
= (3 - x - y)(3 - x + y)
8) x² + 3x + 2
= x² + x + 2x + 2
= (x² + x) + (2x + 2)
= x(x + 1) + 2(x + 1)
= (x + 1)(x + 2)
9) x² - x - 2
= x² + x - 2x - 2
= (x² + x) - (2x + 2)
= x(x + 1) - 2(x + 1)
= (x + 1)(x - 2)
10) x² - x - 6
= x² + 2x - 3x - 6
= (x² + 2x) - (3x + 6)
= x(x + 2) - 3(x + 2)
= (x + 2)(x - 3)

cô làm rồi em ơi https://olm.vn/cau-hoi/bai-3-tu-giac-abcd-co-goc-c-goc-d-90-do-chung-minh-rang-ac2-bd-ab2cd2.8140260328277

\(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)
\(=\dfrac{bxz-cxy}{ax}=\dfrac{cyx-ayz}{by}=\dfrac{azy-bxz}{cz}\)
\(=\dfrac{bxz-cxy+cyx-ayz+azy-bxz}{ax+by+cz}=0\)
\(\Rightarrow bz-cy=0\Rightarrow bz=cy\Rightarrow\dfrac{y}{b}=\dfrac{z}{c}\)
Tương tự...
\(\Rightarrow\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\left(dpcm\right)\)

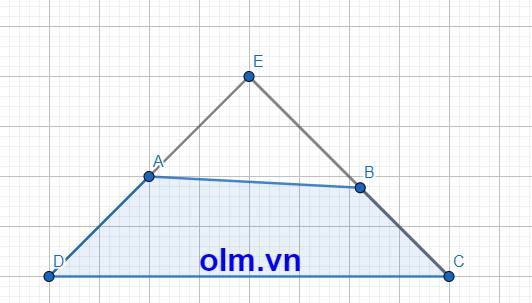
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)

Phân tích đa thức:
x^4 + 2x^3 - x^2 - 2x + 1
= (x^4 + 2x^3) - (x^2 + 2x) + 1
= x^3(x + 2) - x(x + 2) + 1
= (x^3 - x)(x + 2) + 1
= x(x^2 - 1)(x + 2) + 1
= x(x - 1)(x + 1)(x + 2) + 1
Vậy phương trình đã cho có các nghiệm là x = -2, x = -1, x = 0 và x = 1.