Một người đi xe đạp từ A đến B dự định vận tốc 12km/h sau khi được quãng đường đầu thì xe hỏng do đó phải chờ 20 phút quãng đường còn lại người đó đi ô tô với vận tốc 26km/h vì vậy đến B sớm hơn 1h20 phút so với dự định tính quãng đường AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện:
Ta thấy:
=> phương trình đã cho
Vậy phương trình đã cho vô nghiệm
Điều kiện:
Ta thấy:
=> phương trình đã cho
Vậy phương trình đã cho vô nghiệm

đk x >= -4
\(\sqrt{x+4}=-x^4+2x^2-1\Leftrightarrow\sqrt{x+4}=-\left(x^2-1\right)^2\)
Ta có \(\sqrt{x+4}\ge0;-\left(x^2-1\right)^2\le0\)
Vậy pt vô nghiệm

\(\dfrac{\sqrt{15}-\sqrt{20}}{10-\sqrt{75}}\)
\(=\dfrac{\sqrt{15}-2\sqrt{5}}{10-5\sqrt{3}}\)
\(=\dfrac{\sqrt{5}(\sqrt{3}-2)}{-5(\sqrt{3}-2)}\)
\(=\dfrac{-\sqrt{5}}{5}\)
\(=\dfrac{\sqrt{15}-2\sqrt{5}}{10-5\sqrt{3}}=\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{5\left(2-\sqrt{3}\right)}=\dfrac{-\sqrt{5}\left(2-\sqrt{3}\right)}{5\left(2-\sqrt{3}\right)}=\dfrac{-\sqrt{5}}{5}=-\dfrac{1}{\sqrt{5}}\)

Do tam giác ABC đều nên tâm đường tròn ngoại tiếp tam giác này cũng chính là trực tâm của nó. Do đó bạn chỉ cần kẻ 2 đường cao AH, BK của tam giác ABC. Giao điểm của AH và BK chính là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi giao điểm này là O. Tam giác ABC đều nên đường cao AH cũng là đường trung tuyến, đồng thời O là trọng tâm tam giác ABC. Do vậy: \(OA=\dfrac{2}{3}AH\) (*)
Mặt khác, H là trung điểm của cạnh BC nên \(BH=\dfrac{BC}{2}=\dfrac{a}{2}\)
Tam giác ABH vuông tại H nên \(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}=\sqrt{a^2-\dfrac{a^2}{4}}\) \(=\sqrt{\dfrac{3a^2}{4}}=\dfrac{a\sqrt{3}}{2}\)
Thay vào (*), ta có \(OA=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Vậy đường tròn ngoại tiếp tam giác ABC là \(\left(O;\dfrac{a\sqrt{3}}{3}\right)\)

Có: \(\dfrac{a}{\sqrt{a-1}} \ge 2\)
\(<=>\dfrac{a}{\sqrt{a-1}}-2 \ge 0\)
\(<=>\dfrac{a-2\sqrt{a-1}}{\sqrt{a-1}} \ge 0\)
\(<=>\dfrac{(\sqrt{a-1}+1)^2}{\sqrt{a-1}} \ge 0\)
Vì `a > 1=>a-1 > 0<=>\sqrt{a-1} > 0`
\((\sqrt{a-1}+1)^2 \ge 0\)
\(=>\dfrac{(\sqrt{a-1}+1)^2}{\sqrt{a-1}} \ge 0\)
`->Đpcm`
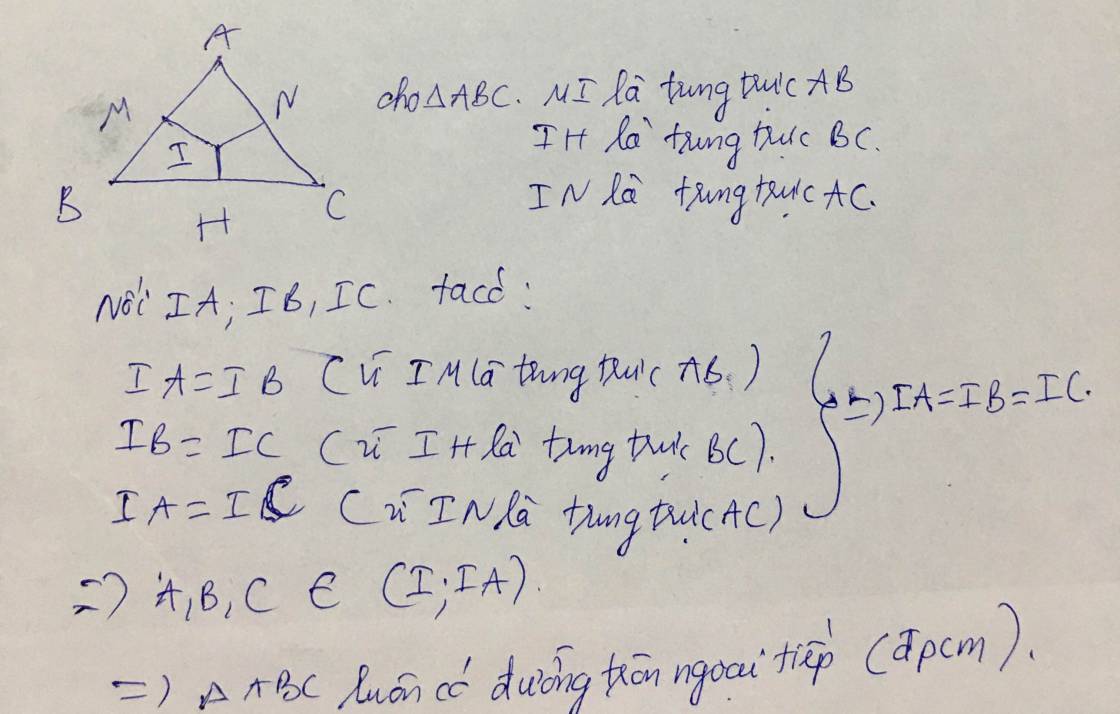
Gọi \(x\left(km\right)\) là độ dài quãng đường AB \(\left(x>0\right)\)
Như vậy quãng đường từ điểm xuất phát đến điểm xe bị hỏng sẽ bằng \(\dfrac{1}{3}x\left(km\right)\)
Thời gian từ khi người đó xuất phát đến khi xe bị hỏng là \(\dfrac{\dfrac{1}{3}x}{12}=\dfrac{1}{36}x\left(h\right)\)
Quãng đường còn lại sẽ bằng \(\dfrac{2}{3}x\left(km\right)\)
Thời gian người đó đi ô tô từ điểm xe bị hỏng đến B là \(\dfrac{\dfrac{2}{3}x}{26}=\dfrac{1}{39}x\left(h\right)\)
Tổng thời gian người đó đã đi từ A đến B trong thực tế là \(\dfrac{1}{36}x+\dfrac{1}{39}x+\dfrac{1}{3}\left(h\right)\) (có số hạng \(\dfrac{1}{3}\) do người đó còn phải chờ \(20p=\dfrac{1}{3}h\) khi xe bị hỏng)
Theo dự định, thời gian người đó đi từ A đến B là \(\dfrac{x}{12}\left(h\right)\)
Vì người đó đến B sớm hơn dự định \(1h20p=\dfrac{4}{3}h\) nên ta có pt \(\dfrac{x}{12}-\left(\dfrac{1}{36}x+\dfrac{1}{39}x+\dfrac{1}{3}\right)=\dfrac{4}{3}\)
\(\Leftrightarrow\left(\dfrac{1}{12}-\dfrac{1}{36}-\dfrac{1}{39}\right)x-\dfrac{1}{3}=\dfrac{4}{3}\)
\(\Leftrightarrow\dfrac{7}{234}x=\dfrac{5}{3}\)
\(\Leftrightarrow x=\dfrac{390}{7}\approx55,714\left(nhận\right)\)
Vậy độ dài quãng đường AB là khoảng \(55,714km\)