Tính tổng của:
150 số chẵn đầu tiên:
có lời giải nhé!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Gọi hai số tự nhiên liên tiếp là 2k;2k+1
2k+2k+1=4k+1 là số lẻ
=>Tổng của hai số tự nhiên liên tiếp là số lẻ
b: Gọi bốn số tự nhiên liên tiếp là a;a+1;a+2;a+3
Tổng của bốn số tự nhiên liên tiếp là:
a+a+1+a+2+a+3=4a+6
\(=4a+4+2=4\left(a+1\right)+2⋮̸4\)
=>Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4

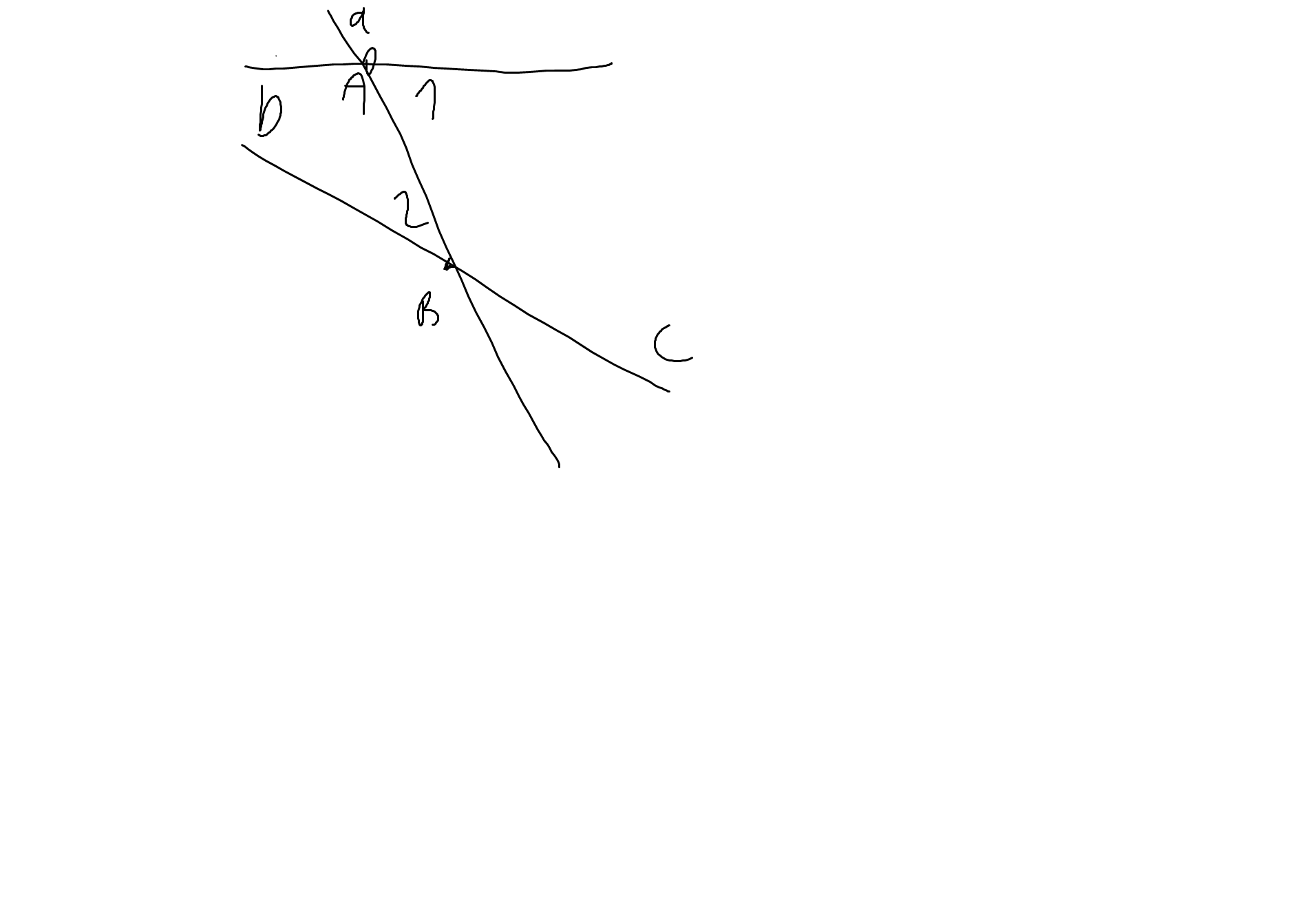
| GT | a cắt b tại A, a cắt c tại B \(\widehat{A_1}\ne\widehat{B_2}\) |
| KL | b cắt c |
Vì \(\widehat{A_1}\ne\widehat{B_2}\)
nên b sẽ không song song với c
mà b và c là hai đường thẳng phân biệt
nên b cắt c

a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BH\cdot BC=BA^2\)
b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)
=>\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE~ΔACB

\(\left(\dfrac{1}{6}+\dfrac{1}{3}\right)^2:\left(1+\dfrac{2}{3}-\dfrac{5}{4}\right)\)
\(=\left(\dfrac{1}{6}+\dfrac{2}{6}\right)^2:\left(\dfrac{12}{12}+\dfrac{8}{12}-\dfrac{15}{12}\right)\)
\(=\left(\dfrac{3}{6}\right)^2:\dfrac{5}{12}=\dfrac{1}{4}\cdot\dfrac{12}{5}=\dfrac{3}{5}\)

1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
=>AD=AE và BD=CE
Xét ΔABC có \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
nên DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
Hình thang BEDC có BD=CE
nên BEDC là hình thang cân
2: Ta có: \(\widehat{DAK}=\widehat{KAB}\)
mà \(\widehat{KAB}=\widehat{AKD}\)
nên \(\widehat{DAK}=\widehat{DKA}\)
=>DA=DK
Ta có: \(\widehat{CBK}=\widehat{ABK}\)
mà \(\widehat{ABK}=\widehat{BKC}\)
nên \(\widehat{CKB}=\widehat{CBK}\)
=>CB=CK
CD=AD+BC
=CK+DK
=>C,K,D thẳng hàng

\(-4x^3+4x^2+x-1\)
\(=-4x^2\left(x-1\right)+\left(x-1\right)\)
\(=\left(x-1\right)\left(1-4x^2\right)=\left(x-1\right)\left(1-2x\right)\left(1+2x\right)\)
\(-4x^3+4x^2+x-1\\ =-4x^2\left(x-1\right)+\left(x-1\right)\\ =\left(x-1\right)\left(1-4x^2\right)\\ =\left(x-1\right)\left[1^2-\left(2x\right)^2\right]\\ =\left(x-1\right)\left(1-2x\right)\left(1+2x\right)\)

\(1045\times x-141\times x+96\times x=25000\)
=>\(x\times\left(1045-141+96\right)=25000\)
=>\(x\times1000=25000\)
=>x=25

Sửa đề: x-2y+3z=-33
10x=6y=5z
=>\(\dfrac{10x}{30}=\dfrac{6y}{30}=\dfrac{5z}{30}\)
=>\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}\)
mà x-2y+3z=-33
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x-2y+3z}{3-2\cdot5+3\cdot6}=\dfrac{-33}{11}=-3\)
=>\(x=-3\cdot3=-9;y=-3\cdot5=-15;z=-3\cdot6=-18\)

a: 4,25; 4,52; 5,42; 5,24; 2,45; 2,54
b: 2,45; 2,54; 4,25; 4,52; 5,24; 5,42
150 số chẵn đầu tiên là 0;2;4;...;298
Tổng của 150 số chẵn đầu tiên là:
(0+298)x150:2=22350
Giải:
Số chẵn đầu tiên là: 0
Khoảng cách giữa các số chẵn liên tiếp là: 2 - 0 = 2
Số chẵn thứ 150 là: 2 x (150 - 1) + 0 = 298
Tổng của 150 số chẵn đầu tiên là: (298 + 0) x 150 : 2 = 22350
Đáp số: 22350