Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: XétΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HB\cdot HC=HA^2\)
c: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>\(\widehat{MAC}=\widehat{ACB}\)
\(\widehat{MAC}+\widehat{AED}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>DE\(\perp\)AM

\(\dfrac{x^2+x+1}{x+1}+\dfrac{x^2+2x+2}{x+2}-\dfrac{x^2+3x+3}{x+3}-\dfrac{x^2+4x+4}{x+4}=0\)
=>\(\dfrac{x\left(x+1\right)+1}{x+1}+\dfrac{x\left(x+2\right)+2}{x+2}-\dfrac{x\left(x+3\right)+3}{x+3}-\dfrac{x\left(x+4\right)+4}{x+4}=0\)
=>\(x+x-x-x+\dfrac{1}{x+1}+\dfrac{2}{x+2}-\dfrac{3}{x+3}-\dfrac{4}{x+4}=0\)
=>\(\left(\dfrac{1}{x+1}-1\right)+\left(\dfrac{2}{x+2}-1\right)-\left(\dfrac{3}{x+3}-1\right)-\left(\dfrac{4}{x+4}-1\right)=0\)
=>\(\dfrac{-x}{x+1}+\dfrac{-x}{x+2}-\dfrac{-x}{x+3}-\dfrac{-x}{x+4}=0\)
=>x=0

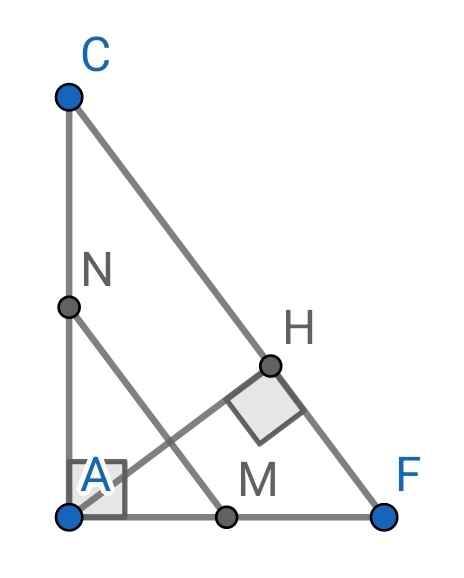
a) Sửa đề: Chứng minh MN là đường trung bình của ∆AFC
Do M là trung điểm của AF (gt)
N là trung điểm của AC (gt)
⇒ MN là đường trung bình của ∆AFC
b) Xét hai tam giác vuông: ∆AFC và ∆HFA có:
∠F chung
⇒ ∆AFC ∽ ∆HFA (g-g)
c) Xét hai tam giác vuông: ∆AHC và ∆FHA có:
∠ACH = ∠FAH (cùng phụ ∠AFC)
⇒ ∆AHC ∽ ∆FHA (g-g)
⇒ AH/HF = HC/AH
⇒ AH² = HF.HC

Bài 3.1:
a: Thay x=1 vào y=2x-1, ta được:
\(y=2\cdot1-1=1\)
vậy: A(1;1)
b: Thay y=-3/2 vào y=2x-1, ta được:
\(2x-1=-\dfrac{3}{2}\)
=>\(2x=-\dfrac{1}{2}\)
=>\(x=-\dfrac{1}{4}\)
Vậy: \(B\left(-\dfrac{1}{4};-\dfrac{3}{2}\right)\)
c:
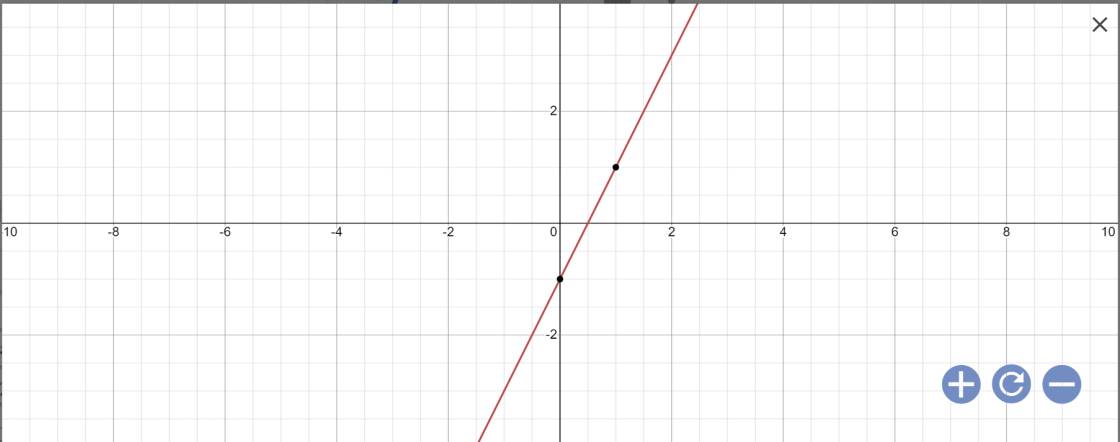
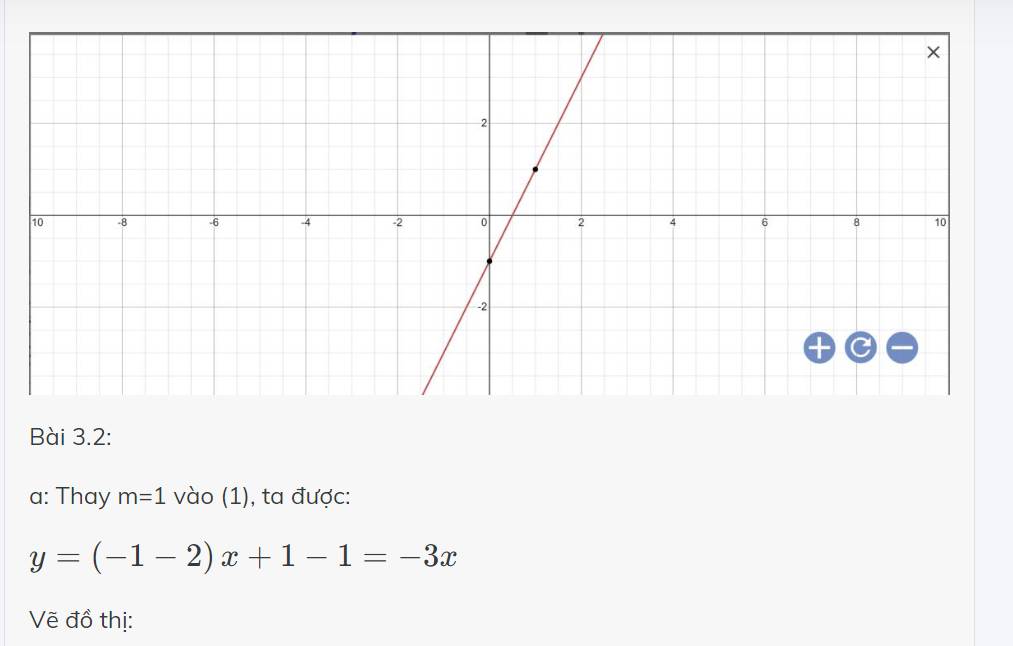
Bài 3.2:
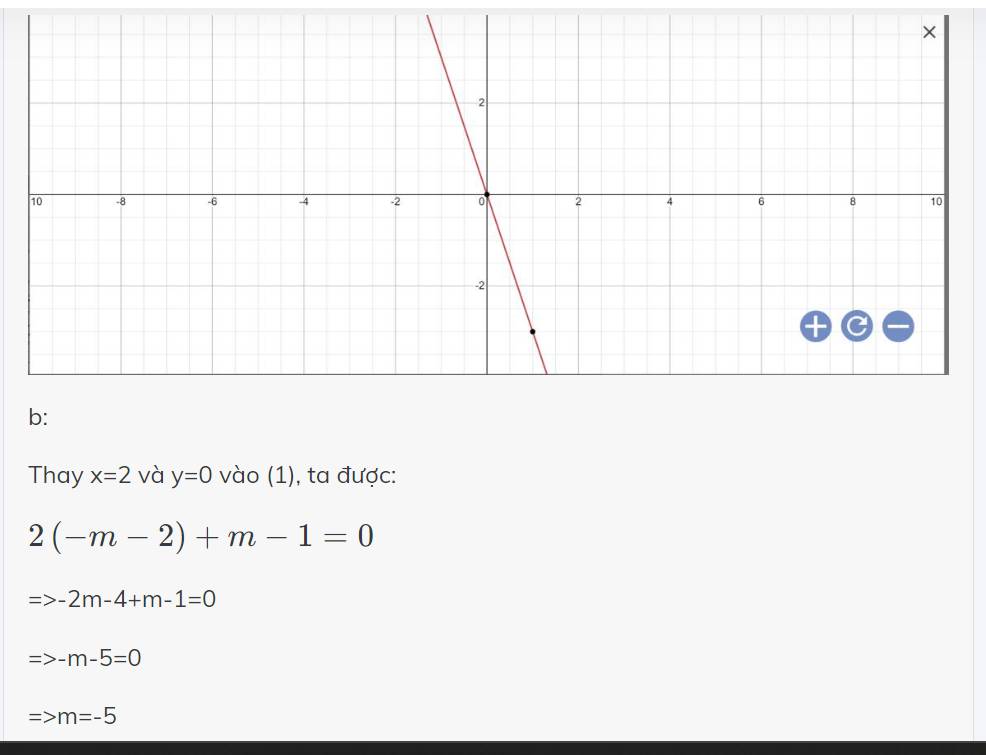
a: Thay m=1 vào (1), ta được:
\(y=\left(-1-2\right)x+1-1=-3x\)
Vẽ đồ thị:
b:
Thay x=2 và y=0 vào (1), ta được:
\(2\left(-m-2\right)+m-1=0\)
=>-2m-4+m-1=0
=>-m-5=0
=>m=-5
c: Thay x=0 và y=2 vào (1), ta được:
\(0\left(-m-2\right)+m-1=2\)
=>m-1=2
=>m=3
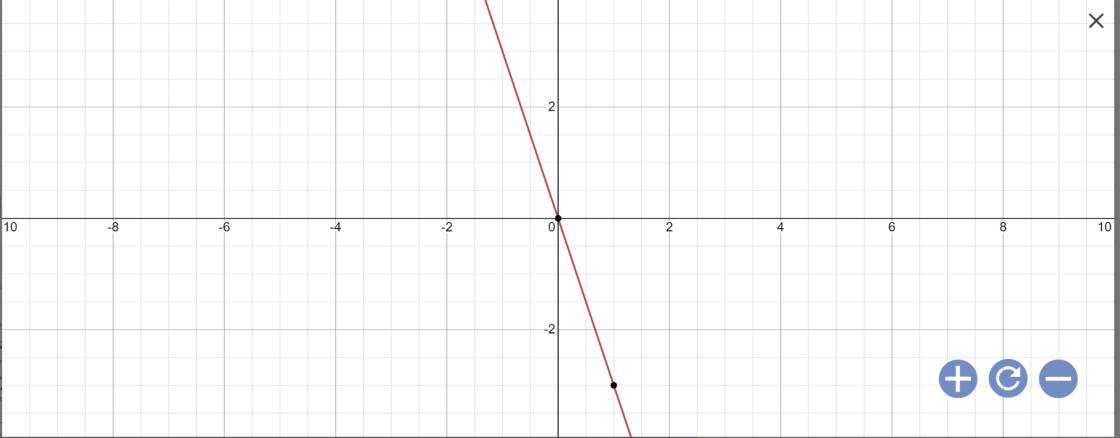
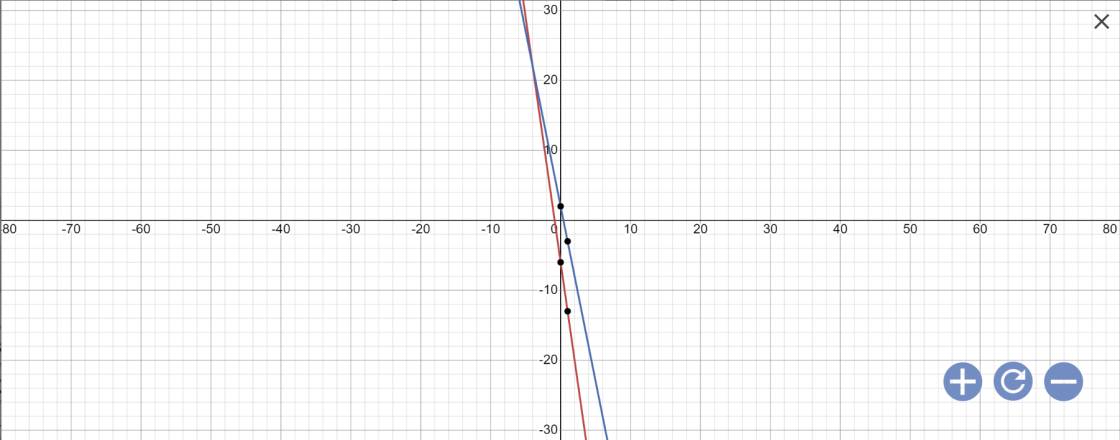
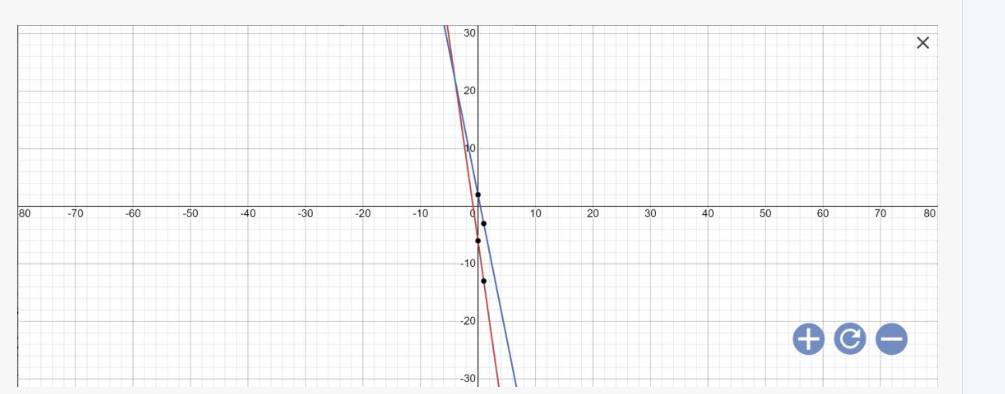
d: Khi m=-5 thì (1): \(y=\left(-5-2\right)x+\left(-5\right)-1=-7x-6\)
Khi m=3 thì (1); \(y=\left(-3-2\right)x+3-1=-5x+2\)
Vẽ đồ thị:

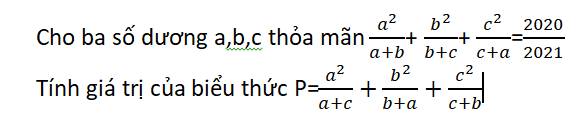

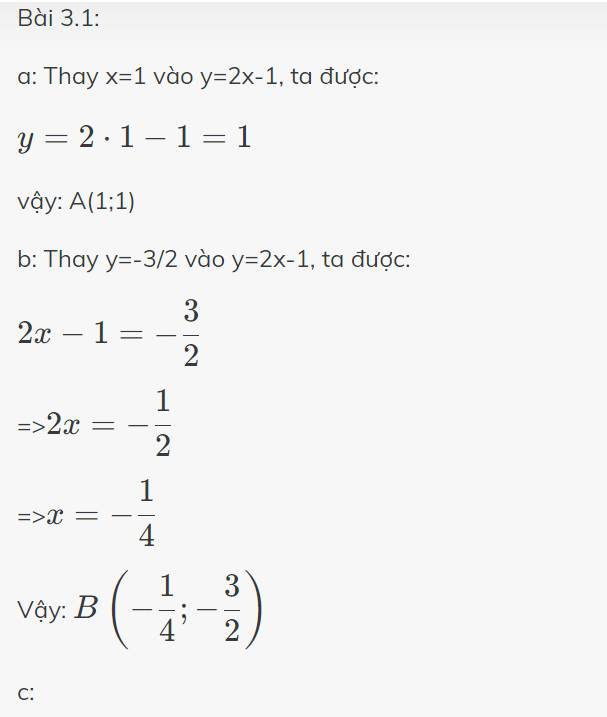

 giúp mình hai câu này với
giúp mình hai câu này với