cho a,b thuộc Z và 3a cộng 4b chia hết cho 7 CMR
A)a+6b chia hết cho 7
B)(a+6b)(2a+5b)(3a+4b)(4a+3b)(5a+2b)(6a+b) chia hết cho 7^6
làm ơn hãy cứu mình :(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
7 tháng 1
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!
7 tháng 1
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 1
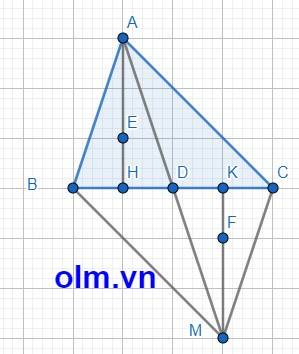
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
K
7 tháng 1
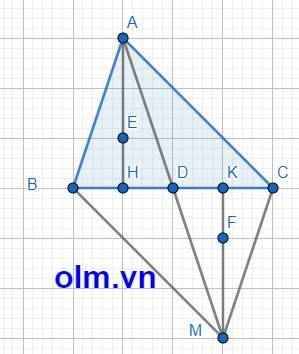
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
Đặt \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}\)
\(\Rightarrow2A-A=1-\dfrac{1}{2^{100}}\)
\(\Rightarrow A=1-\dfrac{1}{2^{100}}< 1\) (đpcm)
A
2
N
1
AH
Akai Haruma
Giáo viên
5 tháng 2
Lời giải:
Gọi $ƯCLN(8n+85, 4n+7)=d$
$\Rightarrow 8n+85\vdots d; 4n+7\vdots d$
$\Rightarrow 8n+85-2(4n+7)\vdots d$
$\Rightarrow 71\vdots d$
Để ps đã cho tối giản thì $4n+7\not\vdots 71$
$\Rightarrow 4n+7-71\not\vdots 7$
$\Rightarrow 4n-64\not\vdots 71$
$\Rightarrow 4(n-16)\not\vdots 71$
$\Rightarrow n-16\not\vdots 71$
$\Rightarrow n\neq 71k+16$ với $k$ là số tự nhiên bất kỳ.
7 tháng 1
đk đã cho \(\Leftrightarrow\)\(8\left(x-2022\right)^2+y^2=25\) (1)
Vì \(\left(x-2022\right)^2\ge0;y^2\ge0\) nên (1) suy ra:
\(8\left(x-2022\right)^2\le25\)
\(\Leftrightarrow\left(x-2022\right)^2\le\dfrac{25}{8}\)
Do \(x\inℤ\) nên suy ra \(\left(x-2022\right)^2\le3\)
\(\Rightarrow x-2022\in\left\{0;\pm1;\pm2;\pm3\right\}\)
\(\Rightarrow x\in\left\{2022;2023;2021;2024;2020;2025;2019\right\}\)
Nếu \(x=2022\Rightarrow y=\pm5\)
Nếu \(x\in\left\{2021;2023\right\}\) thì \(y^2=17\), vô lý.
Nếu \(\left|x-2022\right|\ge2\) thì \(8\left(x-2022\right)^2\ge32\) \(\Leftrightarrow25-y^2\ge32\) \(\Leftrightarrow y^2\le-7\), vô lý.
Vậy có các cặp số (x; y) sau thỏa mãn:
\(\left(2022;5\right),\left(2022;-5\right)\)
KV
7 tháng 1
Do (x - 2022)² ≥ 0 với mọi x R
8(x - 2022)² ≥ 0 với mọi x R
25 - y² ≥ 0
y² ≤ 25
⇒ y ∈ {-5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5}
Do x, y ∈ Z nên (25 - y²) ⋮ 8
⇒ y ∈ {-5; -3; -1; 1; 3; 5}
⇒ (25 - y²) : 8 ∈ {0; 2; 3}
⇒ (x - 2022)² ∈ {0; 2; 3}
⇒ x - 2022 = 0
⇒ x = 2022
Vậy ta tìm được 2 cặp giá trị (x; y) thỏa mãn:
(2022; -5); (2022; 5)
A)Ta có: (3a + 4b) ⋮ 7 ⇒ 2 . (3a + 4b) ⋮ 7 ⇒ (6a + 8b) ⋮ 7 (1)
Ta lại có:
(6a + 8b) + (a + 6b)
=(6a + a) + (8b + 6b)
=7a + 14b
=7a + 7 . 2 . b
=7 . (a + 2b) ⋮ 7 (vì 7 ⋮ 7)
⇒(6a + 8b) + (a + 6b) ⋮ 7 mà (6a + 8b) ⋮ 7 (theo (1))
⇒(a + 6b) ⋮ 7 (ĐPCM)
Vậy...
Xin lỗi anh nhưng câu B) em không hiểu lắm ạ!
B) Làm tương tự câu a ta được:
(a+6b); (2a+5b); (3a+4b); (4a+3b); (5a+2b); (6a+b) đều chia hết cho 7 ⇒(a+6b).(2a+5b).(3a+4b).(4a+3b).(5a+2b).(6a+b) chia hết cho 7.7.7.7.7.7 ⇒(a+6b).(2a+5b).(3a+4b).(4a+3b).(5a+2b).(6a+b) chia hết cho 76 (ĐPCM)
Vậy...