Câu 11:

Số tiền phải trả khi mua 2,5kg nhãn là:

52500:1,5x2,5=87500(đồng)

Câu 12:

32dm=3,2m; 40dm=4m

Thể tích nước đang có trong bể là:

\(5\times3,2\times4\times80\%=51,2\left(m^3\right)\)

Câu 13:

Khối lượng rau năm nay thu hoạch được là:

\(150\left(1+25\%\right)=150\times1,25=187,5\left(kg\right)\)

giúp mik câu 17 thôi nha

+ �=131+132+133+…+160S=311​+321​+331​+…+601​

�<(130+130+…+130)+(140+140+…+140)+(150+150+…+150)S<(301​+301​+…+301​)+(401​+401​+…+401​)+(501​+501​+…+501​)

�<1030+1040+1050<4860=45;S<3010​+4010​+5010​<6048​=54​;

+ �>(140+140+…+140)+(150+150+…+150)+(160+160+…+160)S>(401​+401​+…+401​)+(501​+501​+…+501​)+(601​+601​+…+601​)

�>1040+1050+1060>35.S>4010​+5010​+6010​>53​.

a: Số quả bóng bán được trong tháng 1 là \(3\cdot5=15\left(quả\right)\)

Số quả bóng bán được trong tháng 2 là \(4\cdot5=20\left(quả\right)\)

Số quả bóng bán được trong tháng 3 là \(2\cdot5=10\left(quả\right)\)

b: Tổng số quả bóng rổ bán được trong 3 tháng là:

15+20+10=45(quả)

c: Tháng 2 bán được nhiều hơn tháng 3:

20-10=10(quả)

d: Tỉ số giữa số lượng bóng rổ bán được trong tháng 1 và tháng 2 là:

\(15:20=\dfrac{3}{4}\)

a) Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

$15$ quả; $20$ quả; $10$ quả.

b) Cả ba tháng cửa hàng bán được:

$15+20+10=45$ (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

$20–10=10$ (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

3:4=343:4=43​
 

bài 1:

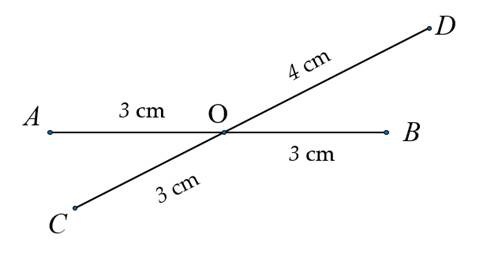
a: O thuộc đoạn AB,CD,OA,OB,OC,OD

b: O là trung điểm của AB

1. a) $O$ thuộc các đoạn thẳng: $AB;CD;OA;OB;OC;OD.$

b) Ta có $O$ nằm giữa hai điểm $A$ và $B$ và $OA=OB=3$ cm nên $O$ là trung điểm của đoạn thẳng $AB.$

2. a) Số đo góc $xOy$ bằng 30∘30∘.

b)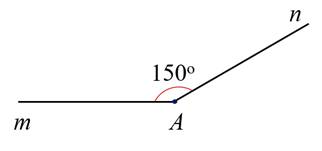 

a) \(\dfrac{5}{17}-\dfrac{25}{31}+\dfrac{12}{17}+\dfrac{-6}{31}\)

\(=\left(\dfrac{5}{17}+\dfrac{12}{17}\right)+\left(\dfrac{-25}{31}+\dfrac{-6}{31}\right)\)

\(=\dfrac{17}{17}+\dfrac{-31}{31}\)

\(=1+\left(-1\right)=0\)

b) \(\dfrac{17}{8}:\left(\dfrac{27}{8}+\dfrac{11}{4}\right)\)

\(=\dfrac{17}{8}:\left(\dfrac{27}{8}+\dfrac{22}{8}\right)\)

\(=\dfrac{17}{8}:\dfrac{49}{8}=\dfrac{17}{8}\cdot\dfrac{8}{49}=\dfrac{17}{49}\)

c) \(\dfrac{1}{5}\cdot\dfrac{11}{16}+\dfrac{1}{5}\cdot\dfrac{5}{16}+\dfrac{4}{5}\)

\(=\dfrac{1}{5}\cdot\left(\dfrac{11}{16}+\dfrac{5}{16}+4\right)\)

\(=\dfrac{1}{5}\cdot\left(\dfrac{16}{16}+4\right)\)

\(=\dfrac{1}{5}\cdot\left(1+4\right)=\dfrac{1}{5}\cdot5=1\)

d) \(\dfrac{5}{6}:25-2+\dfrac{-7}{3}\cdot\dfrac{2}{7}\)

\(=\dfrac{5}{6}\cdot\dfrac{1}{25}-2+\dfrac{-2}{3}\)

\(=\dfrac{1}{30}-\dfrac{6}{3}+\dfrac{-2}{3}\)

\(=\dfrac{1}{30}-\dfrac{8}{3}=\dfrac{1}{30}-\dfrac{80}{30}=\dfrac{-79}{30}\)

a) 517−2531+1217+−631175​−3125​+1712​+31−6​

=517−2531+1217+−631=175​−3125​+1712​+31−6​

=(517+1217)+(−2531+−631)=(175​+1712​)+(−3125​+31−6​)

$=1+(-1)$

$=0$

b) 178:(278+114)817​:(827​+411​)

=178:(278+228)=817​:(827​+822​)

=178:498=817​:849​

=1749=4917​.

c) 15⋅1116+15⋅516+4551​⋅1611​+51​⋅165​+54​

=15⋅(1116+516)+45=51​⋅(1611​+165​)+54​

=15⋅1+45=51​⋅1+54​

=15+45=1.=51​+54​=1.

d) 56:25−2+−73⋅2765​:25−2+3−7​⋅72​

=56:25−2+−73⋅27=65​:25−2+3−7​⋅72​

=56⋅125−2+−23=65​⋅251​−2+3−2​

=130−2+−23=301​−2+3−2​

=130−6030+−2030=301​−3060​+30−20​

=130−6030+−2030=−7930=301​−3060​+30−20​=30−79​
 

a: Xét (O) có

ΔAKB nội tiếp

AB là đường kính

Do đó: ΔAKB vuông tại K

=>AK\(\perp\)MB tại K

Xét tứ giác AIKM có \(\widehat{AIM}=\widehat{AKM}=90^0\)

nên AIKM là tứ giác nội tiếp

b: Ta có: AIKM là tứ giác nội tiếp

=>\(\widehat{MIK}=\widehat{MAK}\)

mà \(\widehat{MAK}=\widehat{KBA}\left(=90^0-\widehat{KAB}\right)\)

nên \(\widehat{MIK}=\widehat{KBA}\)

=>\(\widehat{KBO}+\widehat{KIO}=180^0\)

=>KIOB là tứ giác nội tiếp

a: Phương trình hoành độ giao điểm là:

\(x^2=3x-2\)

=>\(x^2-3x+2=0\)

=>(x-1)(x-2)=0

=>\(\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

Khi x=1 thì \(y=1^2=1\)

Khi x=2 thì \(y=2^2=4\)

Vậy: A(1;1); B(2;4)

b: O(0;0); A(1;1); B(2;4)

\(OA=\sqrt{\left(1-0\right)^2+\left(1-0\right)^2}=\sqrt{2}\)

\(OB=\sqrt{\left(2-0\right)^2+\left(4-0\right)^2}=2\sqrt{5}\)

\(AB=\sqrt{\left(2-1\right)^2+\left(4-1\right)^2}=\sqrt{3^2+1}=\sqrt{10}\)

Xét ΔOAB có \(cosOAB=\dfrac{AO^2+AB^2-OB^2}{2\cdot AO\cdot AB}=\dfrac{2+10-20}{2\cdot\sqrt{2}\cdot\sqrt{10}}=\dfrac{-2\sqrt{5}}{5}\)

=>\(sinOAB=\sqrt{1-\left(-\dfrac{2\sqrt{5}}{5}\right)^2}=\dfrac{1}{\sqrt{5}}\)

Diện tích tam giác OAB là:

\(S_{OAB}=\dfrac{1}{2}\cdot AO\cdot AB\cdot sinOAB\)

\(=\dfrac{1}{2}\cdot\sqrt{2}\cdot\sqrt{10}\cdot\dfrac{1}{\sqrt{5}}=1\)

Gọi số sản phẩm tổ 1 được giao theo kế hoạch là x(sản phẩm)

(Điều kiện: \(x\in Z^+\))
SỐ sản phẩm tổ 2 được giao theo kế hoạch là 

1100-x(sản phẩm)

Số sản phẩm tổ 1 làm được là: \(x\left(1+18\%\right)=1,18x\left(sảnphẩm\right)\)

Số sản phẩm tổ 2 làm được:

\(\left(1100-x\right)\left(1+15\%\right)=1,15\left(1100-x\right)\left(sảnphẩm\right)\)

Hai đội vượt mức 180 sản phẩm nên ta có:

1,18x+1,15(1100-x)=1100+180

=>0,03x+1265=1280

=>0,03x=15

=>x=500(nhận)

Vậy: Số sản phẩm tổ 1 được giao theo kế hoạch là 500 sản phẩm, tổ 2 được giao là 1100-500=600 sản phẩm

a: Thay x=4 vào P, ta được:

\(P=\dfrac{4+7}{3\cdot2}=\dfrac{11}{6}\)

b: \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{7\sqrt{x}+3}{9-x}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{7\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+2\sqrt{x}\left(\sqrt{x}-3\right)-7\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{x+4\sqrt{x}+3+2x-6\sqrt{x}-7\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+3}\)

c: \(A=P\cdot Q=\dfrac{3\sqrt{x}}{\sqrt{x}+3}\cdot\dfrac{x+7}{3\sqrt{x}}=\dfrac{x+7}{\sqrt{x}+3}\)

\(=\dfrac{x-9+16}{\sqrt{x}+3}=\sqrt{x}-3+\dfrac{16}{\sqrt{x}+3}\)

\(=\sqrt{x}+3+\dfrac{16}{\sqrt{x}+3}-6>=2\cdot\sqrt{\left(\sqrt{x}+3\right)\cdot\dfrac{16}{\sqrt{x}+3}}-6=2\cdot4-6=2\)

Dấu '=' xảy ra khi \(\sqrt{x}+3=\sqrt{16}=4\)

=>x=1