
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


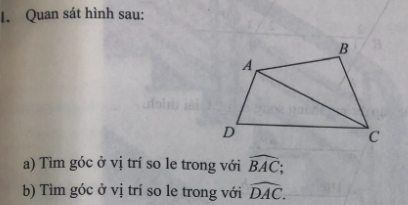
a: Góc so le trong với \(\widehat{BAC}\) là góc ACD
b: Góc so le trong với \(\widehat{DAC}\) là góc BCA

Chiều rộng của thửa ruộng là:
\(160\times\dfrac{5}{8}=100\left(m\right)\)
Diện tích của thửa ruộng là:
\(160\times100=16000\left(m^2\right)\)
ĐS: ...
chiều rộng của thửa ruộng hình chữ nhật đó là
160 . 5/8 = 100 (m)
diện tích của thửa ruộng hình chữ nhật đó là
160 . 100 = 16000 ( m^2)
Đ/s 16000 m vuông

\(M=4^{40}\left(1+4+4^2\right)=4^{40}.21=2^{80}.21=2^{77}.8.21=\)
\(=2^{77}.8.7.3=2^{77}.56.3⋮56\)

Bài 5:
a) Oc nằm giữa Oa và Ob
=> \(\widehat{aOb}=\widehat{aOc}+\widehat{cOb}\)
\(=>\widehat{cOb}=\widehat{aOb}-\widehat{aOc}=100^o-40^o=60^o\)
b) Od là phân giác của \(\widehat{cOb}\)
=> \(\widehat{cOd}=\widehat{dOb}\)
Mà: \(\widehat{cOd}+\widehat{dOb}=\widehat{cOb}=>2\widehat{cOd}=60^o\)
\(=>\widehat{cOd}=\dfrac{60^o}{2}=30^o\)
6:
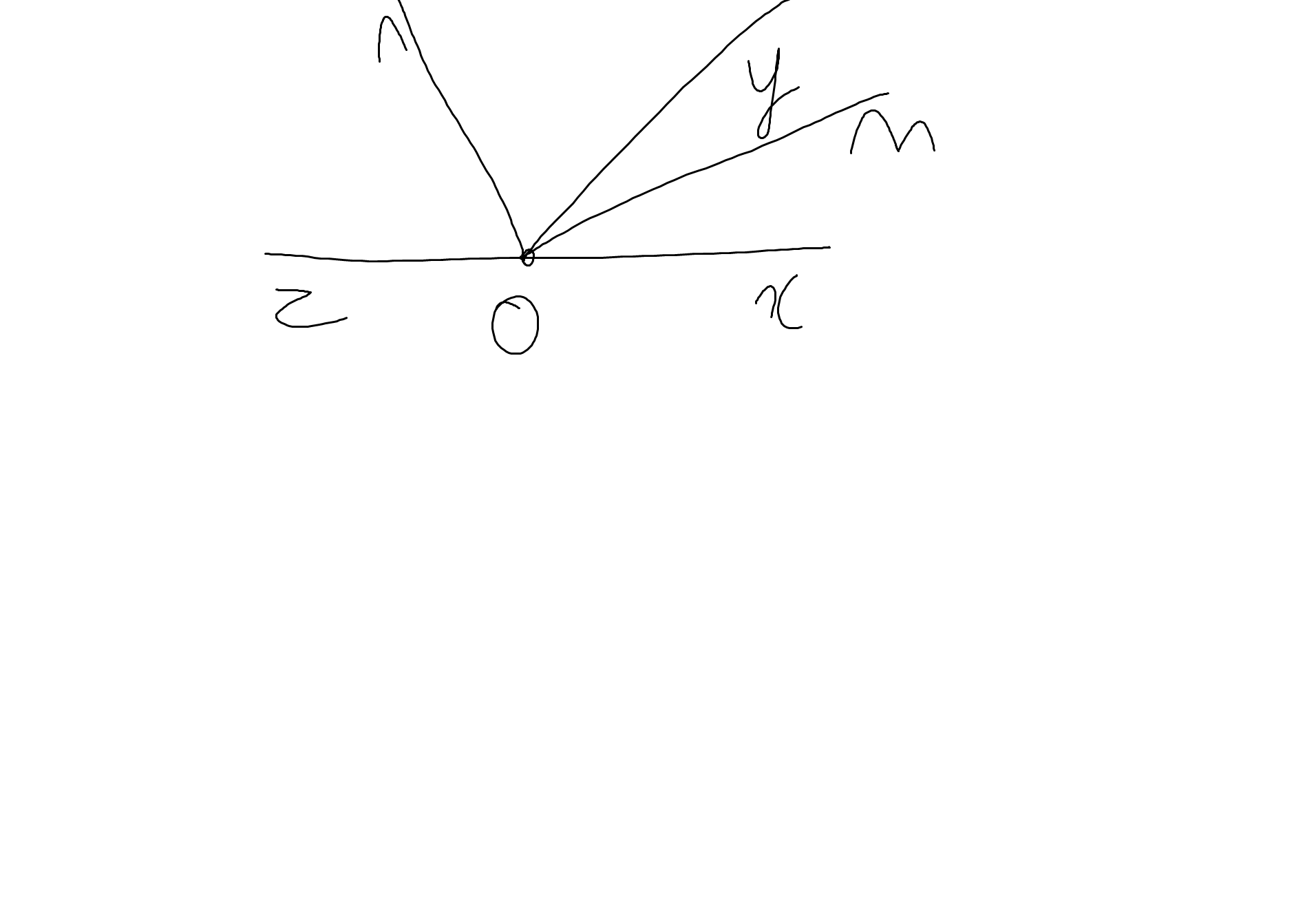
Ta có: \(\widehat{xOy}+\widehat{zOy}=180^0\)
=>\(\widehat{zOy}=180^0-60^0=120^0\)
Om là phân giác của góc xOy
=>\(\widehat{yOm}=\dfrac{\widehat{xOy}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: On là phân giác của góc yOz
=>\(\widehat{yOn}=\dfrac{\widehat{yOz}}{2}=\dfrac{120^0}{2}=60^0\)
\(\widehat{mOn}=\widehat{yOm}+\widehat{yOn}=30^0+60^0=90^0\)

\(A=\left(x+2\right)^2+\left(x-2\right)^2\\ =x^2+4x+4+x^2-4x+4\\ =2x^2+8\)
Thay `x=-1/2` vào A ta có:
\(A=2\cdot\left(-\dfrac{1}{2}\right)^2+8=2\cdot\dfrac{1}{4}+8=\dfrac{1}{2}+8=\dfrac{17}{2}\)
\(B=\left(3x-2\right)^2-\left(3x+5\right)^2\\ =\left(3x-2-3x-5\right)\left(3x-2+3x+5\right)\\ =-7\left(6x+3\right)\)
Thay `x=-4` vào B ta có:
\(B=-7\cdot\left(6\cdot-4+3\right)=-7\cdot-21=147\)
\(C=\left(2x+5y\right)^2-5y\left(4x+5y\right)\\ =4x^2+20xy+25y^2-20xy-25y^2\\ =4x^2\)
Thay `x=-1/2;y=-756` vào C ta có:
\(C=4\cdot\left(-\dfrac{1}{2}\right)^2=4\cdot\dfrac{1}{4}=1\)
\(D=\left(x+5\right)^2-\left(x-3\right)^2\\ =\left(x+5-x+3\right)\left(x+5+x-3\right)\\ =8\left(2x+2\right)\)
Thay `x=-3/4` vào D ta có:
\(D=8\cdot\left(2\cdot\dfrac{-3}{4}+2\right)=8\cdot\left(-\dfrac{3}{2}+2\right)=8\cdot\dfrac{1}{2}=4\)

a: Ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
b: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{BAE}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
c: ΔAEB=ΔADC
=>\(\widehat{AEB}=\widehat{ADC}\)
mà \(\widehat{AEB}+\widehat{CEB}=180^0\)(hai góc kề bù) và \(\widehat{ADC}+\widehat{CDB}=180^0\)(hai góc kề bù)
nên \(\widehat{CEB}=\widehat{CDB}\)
ΔAEB=ΔADC
=>\(\widehat{ABE}=\widehat{ACD}\)
Xét ΔIDB và ΔIEC có
\(\widehat{IDB}=\widehat{IEC}\)
DB=EC
\(\widehat{IBD}=\widehat{ICE}\)
Do đó: ΔIDB=ΔIEC
d: Ta có: ΔIDB=ΔIEC
=>IB=IC
Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
Do đó: ΔAIB=ΔAIC
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC
e: Ta có: IB=IC
=>I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
=>AI\(\perp\)BC
f: BD=DE
=>ΔDEB cân tại D
=>\(\widehat{DEB}=\widehat{DBE}\)
mà \(\widehat{DEB}=\widehat{EBC}\)(DE//BC)
nên \(\widehat{ABE}=\widehat{CBE}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
Ta có: DE=EC
=>ΔEDC cân tại E
=>\(\widehat{ECD}=\widehat{EDC}\)
mà \(\widehat{EDC}=\widehat{DCB}\)(ED//BC)
nên \(\widehat{ACD}=\widehat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác kẻ từ C xuống AB

\(51^2=\left(50+1\right)^2=50^2+2\cdot50\cdot1+1^2\\ =2500+100+1=2601\\ 502^2=\left(500+2\right)^2=500^2+2\cdot500\cdot2+2^2\\ =250000+2000+4=252004\\ 98^2=\left(100-2\right)^2=100^2-2\cdot100\cdot2+2^2\\ =10000-400+4 =9604\\ 199^2=\left(200-1\right)^2=200^2-2\cdot200\cdot1+1^2\\ =40000-400+1=39601\)

\(25x^2+10x+4\\ =\left(25x^2+10x+1\right)+3\\ =\left[\left(5x\right)^2+2\cdot5x\cdot1+1^2\right]+3\\ =\left(5x+1\right)^2+3\)
Ta có: `(5x+1)^2>=0` với mọi x
`=>(5x+1)^2+3>=3>0` với mọi x
`=>` Đpcm

\(a.4+12x+9x^2\\ =2^2+2\cdot2\cdot3x+\left(3x\right)^2\\ =\left(2+3x\right)^2\\ b.25+4a^2+10a\\ =5^2+2\cdot5\cdot2a+\left(2a\right)^2\\ =\left(5+2a\right)^2\\ c.14y+y^2+49\\ =y^2+2\cdot y\cdot7+7^2\\ =\left(y+7\right)^2\\ d.9x^2+y^2-6xy\\ =\left(3x\right)^2-2\cdot3x\cdot y+y^2\\ =\left(3x-y\right)^2\)



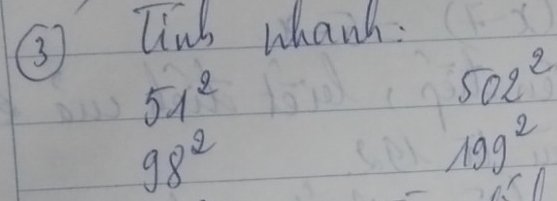

Bài 1:
7) Ta có:
\(28=2^2\cdot7\\ 77=7\cdot11\\ 45=3^2\cdot5\\ =>ƯC\left(28;77;45\right)=1\)
8) Ta có:
\(16=2^4\\ 40=2^3\cdot5\\ 176=2^4\cdot11\\ =>ƯC\left(16;40;176\right)=2^3=8\)
9) Ta có:
\(72=2^3\cdot3^2\\ 36=2^2\cdot3^2\\ 180=2^2\cdot3^2\cdot5\\ =>ƯC\left(72;36;180\right)=2^2\cdot3^2=36\)
10) Ta có:
\(24=2^3\cdot3\\ 96=2^5\cdot3\\ 270=3^3\cdot2\cdot5\\ =>ƯC\left(24;96;270\right)=2\cdot3=6\)
11) Ta có:
\(36=2^2\cdot3^2\\ 80=2^4\cdot5\\ 156=3\cdot13\cdot2^2\)
\(=>ƯC\left(36;80;156\right)=2^2=4\)
12) Ta có:
\(200=2^3\cdot5^2\\ 245=5\cdot7^2\\ 125=5^3\\ =>ƯC\left(200;245;125\right)=5\)
Bài 3:
144 = 24.32
192 = 26.3
ƯCLN(144; 192) = 24.3 = 48
Ư(48) = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48}
Ước chung lớn hơn 20 của 144 và 192 là: 24; 48