Có hai tổ công nhân làm đường biết tổ 1 làm được bằng 3/4 đoạn đường tổ 2 làm được. Nếu tổ 2 làm ít đi 8m, tổ một làm thêm 8m thì lúc này, đoạn đường tổ 2 bằng 6/5 đoạn đường tổ 1 làm. Tính đoạn đường mỗi tổ làm được
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


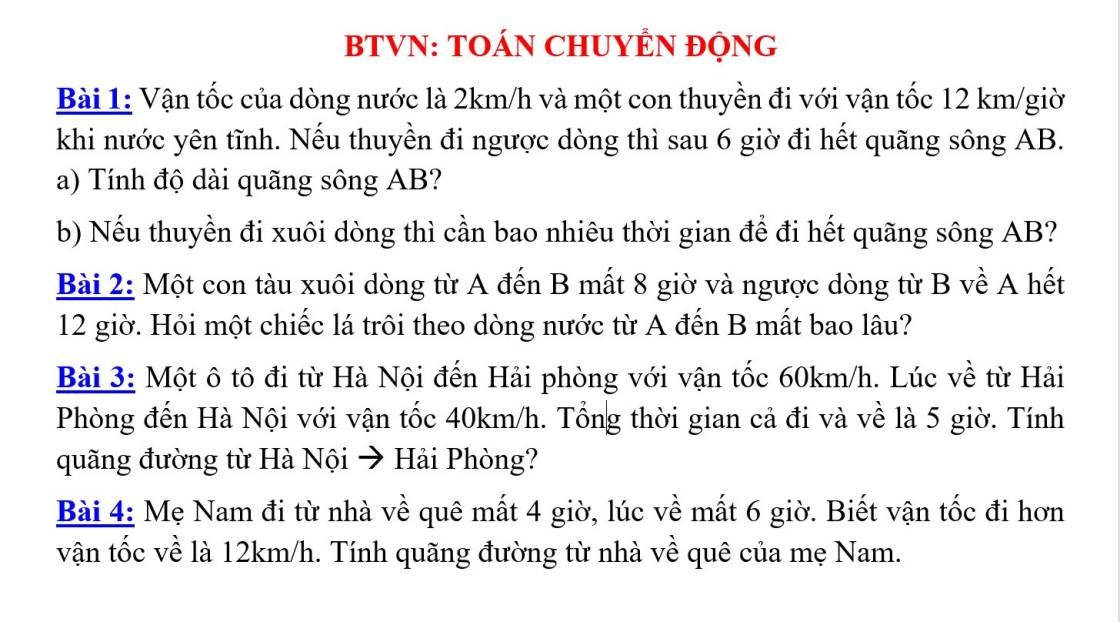
Bài 1:
a. Thuyền đi ngược dòng với vận tốc là:
$12-2=10$ (km/h)
Độ dài quãng sông AB là: $10\times 6=60$ (km)
b. Thuyền xuôi dòng với vận tốc là:
$12+2=14$ (km/h)
Thuyền cần số giờ để đi hết quãng sông AB là:
$60:14\approx 4,29$ (giờ)
Bài 2:
Gọi vận tốc chiếc lá trôi theo dòng sông là $x$ (km/h) và vận tốc thực của con tàu là $a$ (km/h)
Vận tốc xuôi dòng: $a+x=AB:8$
Vận tốc ngược dòng: $a-x=AB:12$
$(a+x)-(a-x)=AB:8-AB:12$
$2\times x=AB\times \frac{1}{8}-AB\times \frac{1}{12}$
$2\times x=AB\times (\frac{1}{8}-\frac{1}{12})$
$2\times x=AB\times \frac{1}{24}$
$AB=2\times x\times 24=x\times 48$
Thời gian chiếc lá trôi từ A - B là: $AB:x=48$ (giờ)


\(X\times9,99+X:100=1000\\ X\times9,99+X\times0,01=1000\\ X\times\left(9,99+0,01\right)=1000\\ X\times10=1000\\ X=\dfrac{1000}{10}=100\)

Thanh sắt cùng loại dài 0,15m nặng:
16: 0,8 x 0,15 = 3(kg)
Đ.số: 3 kg

Lời giải:
$3^{2015}+3^{100}=3^{100}(3^{1915}+1)$
Ta thấy:
$3^3\equiv 1\pmod {13}$
$\Rightarrow 3^{1915}=(3^3)^{638}.3\equiv 1^{638}.3\equiv 3\pmod {13}$
$\Rightarrow 3^{1915}+1\equiv 4\pmod {13}$
Ta thấy: $3^{100}\not\vdots 13; 3^{1915}+1\not\vdots 13$
$\Rightarrow 3^{100}(3^{1915}+1)\not\vdots 13$
Bạn xem lại đề.

Lời giải:
Ta có:
$x+10^0+x+20^0+x+30^0=360^0$
$\Rightarrow 3x+60^0=360^0$
$\RIghtarrow x=100^0$
$\widehat{ABC}=\frac{1}{2}\text{sđc(AC)}=\frac{1}{2}(x+30^0)=\frac{1}{2}(100^0+30^0)=65^0$
$\widehat{ACB}=\frac{1}{2}\text{sđc(AB)}=\frac{1}{2}(x+10^0)=\frac{1}{2}(100^0+10^0)=55^0$
$\widehat{BAC}=180^0-\widehat{ABC}-\widehat{ACB}=180^0-65^0-55^0=60^0$