Cho A = 2 + 2 mũ 2 + 2 mũ 3 + .... + 2 mũ 60 a ) Thu gọn tổng A b) Chứng minh rằng : A chia hết cho 3,5, 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (cuốn) là số sách cần tìm (x ∈ ℕ* và 99 < x < 1000)
Do khi xếp thành từng bó 18 cuốn, 22 cuốn, 24 cuốn đều thừa ra 5 cuốn nên x - 5 ∈ BC(18; 22; 24)
Ta có:
18 = 2.3²
22 = 2.11
24 = 2³.3
⇒ BCNN(18; 22; 24) = 2³.3².11 = 792
⇒ x - 5 ∈ BC(18; 22; 24) = B(792) = {0; 792; 1584; ...}
⇒ x ∈ {5; 797; 1589; ...}
Mà 99 < x < 1000
⇒ x = 797
Vậy số cuốn sách cần tìm là 797 cuốn


15,120 là số thập phân có 3 chữ số ở phần thập phân em nhé.

Theo thầy thì vào tất cả các bài trong HKI nhé em

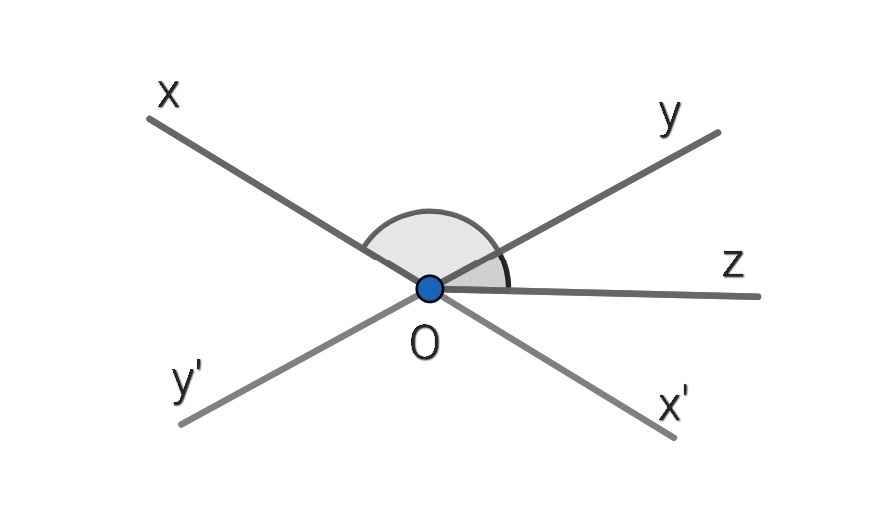 a) Ta có:
a) Ta có:
∠xOy + ∠yOz = 150⁰
∠xOy - ∠yOz = 90⁰
⇒ ∠xOy = (150⁰ + 90⁰) : 2 = 120⁰
⇒ ∠yOz = 120⁰ - 90⁰ = 30⁰
b) Ta có:
∠xOy + ∠x'Oy = 180⁰ (kề bù)
⇒ ∠x'Oy = 180⁰ - ∠xOy
= 180⁰ - 120⁰
= 60⁰

√0,81.(√x - 16/25) = 9/10
0,9.(√x - 16/25) = 9/10
√x - 16/25 = 9/10 : 0,9
√x - 16/25 = 1
√x = 1 + 16/25
√x = 41/25
x = 1681/625 (nhận)
Vậy x = 1681/625

\(\sqrt{0,81}\left(\sqrt{x}-\dfrac{16}{25}\right)=\dfrac{9}{10}\left(x\ge0\right)\\ \Leftrightarrow\sqrt{\dfrac{81}{100}}.\left(\sqrt{x}-\dfrac{16}{25}\right)=\dfrac{9}{10}\\ \Leftrightarrow\dfrac{\sqrt{81}}{\sqrt{100}}.\left(\sqrt{x}-\dfrac{16}{25}\right)=\dfrac{9}{10}\\ \Leftrightarrow\dfrac{9}{10}.\left(\sqrt{x}-\dfrac{16}{25}\right)=\dfrac{9}{10}\\ \Leftrightarrow\sqrt{x}-\dfrac{16}{25}=1\\ \Leftrightarrow\sqrt{x}=\dfrac{41}{25}\\ \Leftrightarrow x=\dfrac{1681}{625}\)
Vậy x = \(\dfrac{1681}{625}\)
a) \(A=2+2^2+2^3+\dots+2^{60}\)
\(2A=2^2+2^3+2^4+\dots+2^{61}\)
\(2A-A=\left(2^2+2^3+2^4+\dots+2^{61}\right)-\left(2+2^2+2^3+\dots+2^{60}\right)\)
\(A=2^{61}-2\)
Vậy: \(A=2^{61}-2\).
b)
+) \(A=2+2^2+2^3+\dots+2^{60}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+\left(2^5+2^6\right)+\dots+\left(2^{59}+2^{60}\right)\)
\(=2\cdot\left(1+2\right)+2^3\cdot\left(1+2\right)+2^5\cdot\left(1+2\right)+\dots+2^{59}\cdot\left(1+2\right)\)
\(=2\cdot3+2^3\cdot3+2^5\cdot3+\dots+2^{59}\cdot3\)
\(=3\cdot\left(2+2^3+2^5+\dots+2^{59}\right)\)
Vì \(3\cdot\left(2+2^3+2^5+\dots+2^{59}\right)⋮3\) nên \(A⋮3\)
+) \(A=2+2^2+2^3+\dots+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+\left(2^9+2^{10}+2^{11}+2^{12}\right)+\dots+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\cdot\left(1+2+2^2+2^3\right)+2^5\cdot\left(1+2+2^2+2^3\right)+2^9\cdot\left(1+2+2^2+2^3\right)+\dots+2^{57}\cdot\left(1+2+2^2+2^3\right)\)
\(=2\cdot15+2^5\cdot15+2^9\cdot15+\dots+2^{57}\cdot15\)
\(=15\cdot\left(2+2^5+2^9+\dots+2^{57}\right)\)
Vì \(15⋮5\) nên \(15\cdot\left(2+2^5+2^9+\dots+2^{57}\right)⋮5\)
hay \(A\vdots5\)
+) \(A=2+2^2+2^3+\dots+2^{60}\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+\left(2^7+2^8+2^9\right)+\dots+\left(2^{58}+2^{59}+2^{60}\right)\)
\(=2\cdot\left(1+2+2^2\right)+2^4\cdot\left(1+2+2^2\right)+2^7\cdot\left(1+2+2^2\right)+\dots+2^{58}\cdot\left(1+2+2^2\right)\)
\(=2\cdot7+2^4\cdot7+2^7\cdot7+\dots+2^{58}\cdot7\)
\(=7\cdot\left(2+2^4+2^7+\dots+2^{58}\right)\)
Vì \(7\cdot\left(2+2^4+2^7+\dots+2^{58}\right)⋮7\) nên \(A⋮7\)
$Toru$
a) �=2+22+23+⋯+260A=2+22+23+⋯+260
2�=22+23+24+⋯+2612A=22+23+24+⋯+261
2�−�=(22+23+24+⋯+261)−(2+22+23+⋯+260)2A−A=(22+23+24+⋯+261)−(2+22+23+⋯+260)
�=261−2A=261−2
Vậy: �=261−2A=261−2.
b)
+) �=2+22+23+⋯+260A=2+22+23+⋯+260
=(2+22)+(23+24)+(25+26)+⋯+(259+260)=(2+22)+(23+24)+(25+26)+⋯+(259+260)
=2⋅(1+2)+23⋅(1+2)+25⋅(1+2)+⋯+259⋅(1+2)=2⋅(1+2)+23⋅(1+2)+25⋅(1+2)+⋯+259⋅(1+2)
=2⋅3+23⋅3+25⋅3+⋯+259⋅3=2⋅3+23⋅3+25⋅3+⋯+259⋅3
=3⋅(2+23+25+⋯+259)=3⋅(2+23+25+⋯+259)
Vì 3⋅(2+23+25+⋯+259)⋮33⋅(2+23+25+⋯+259)⋮3 nên �⋮3A⋮3
+) �=2+22+23+⋯+260A=2+22+23+⋯+260
=(2+22+23+24)+(25+26+27+28)+(29+210+211+212)+⋯+(257+258+259+260)=(2+22+23+24)+(25+26+27+28)+(29+210+211+212)+⋯+(257+258+259+260)
=2⋅(1+2+22+23)+25⋅(1+2+22+23)+29⋅(1+2+22+23)+⋯+257⋅(1+2+22+23)=2⋅(1+2+22+23)+25⋅(1+2+22+23)+29⋅(1+2+22+23)+⋯+257⋅(1+2+22+23)
=2⋅15+25⋅15+29⋅15+⋯+257⋅15=2⋅15+25⋅15+29⋅15+⋯+257⋅15
=15⋅(2+25+29+⋯+257)=15⋅(2+25+29+⋯+257)
Vì 15⋮515⋮5 nên 15⋅(2+25+29+⋯+257)⋮515⋅(2+25+29+⋯+257)⋮5
hay �⋮5A⋮5
+) �=2+22+23+⋯+260A=2+22+23+⋯+260
=(2+22+23)+(24+25+26)+(27+28+29)+⋯+(258+259+260)=(2+22+23)+(24+25+26)+(27+28+29)+⋯+(258+259+260)
=2⋅(1+2+22)+24⋅(1+2+22)+27⋅(1+2+22)+⋯+258⋅(1+2+22)=2⋅(1+2+22)+24⋅(1+2+22)+27⋅(1+2+22)+⋯+258⋅(1+2+22)
=2⋅7+24⋅7+27⋅7+⋯+258⋅7=2⋅7+24⋅7+27⋅7+⋯+258⋅7
=7⋅(2+24+27+⋯+258)=7⋅(2+24+27+⋯+258)
Vì 7⋅(2+24+27+⋯+258)⋮77⋅(2+24+27+⋯+258)⋮7 nên �⋮7A⋮7