dũng có 20 viên

hùng có 16 viên
minh có 8 viên
hc tốt nha

@Phùng Minh Phúc, bạn giải chi tiết ra nhé!

Bạn cần tham gia các hỏi đáp, giúp tất cả mọi người trên diễn đàn, nếu chăm chỉ được lên bảng xếp hạng hỏi đáp mà đứng nhất, nhì, ba... sẽ nhận được xu với các mệnh giá như 500, 400, 300xu.

Hoặc bạn có thể tham gia các sự kiện của cô Thương Hoài tổ chức để có cơ hội được trúng giải. Cũng có thể bạn tham gia fun english, văn hay mỗi tuần, toán vui mỗi tuần, nếu mà bạn làm được đúng và nhanh nhất thì bạn có thể nhận được giải nhé.

Nói chung bạn cần tích cực và hãy luôn sẵn sàng giúp đỡ mn nha, phép màu sẽ đến với bn ^^

Bạn cần tham gia các hỏi đáp, giúp tất cả mọi người trên diễn đàn, nếu chăm chỉ được lên bảng xếp hạng hỏi đáp mà đứng nhất, nhì, ba... sẽ nhận được xu với các mệnh giá như 500, 400, 300xu.

Hoặc bạn có thể tham gia các sự kiện của cô Thương Hoài tổ chức để có cơ hội được trúng giải. Cũng có thể bạn tham gia fun english, văn hay mỗi tuần, toán vui mỗi tuần, nếu mà bạn làm được đúng và nhanh nhất thì bạn có thể nhận được giải nhé.

hnghiaa212.

x= 3 thì y = 4 => \(\dfrac{x}{y}=\dfrac{3}{4}\)

=> khi x= -3/2 thì : \(\dfrac{-\dfrac{3}{2}}{y}=\dfrac{3}{4}\) 

                        <=> 3y = -3/2 * 4 

                       <=>  3y = -6    

                       <=> y = -2  

Chọn \(B:y=-2\)

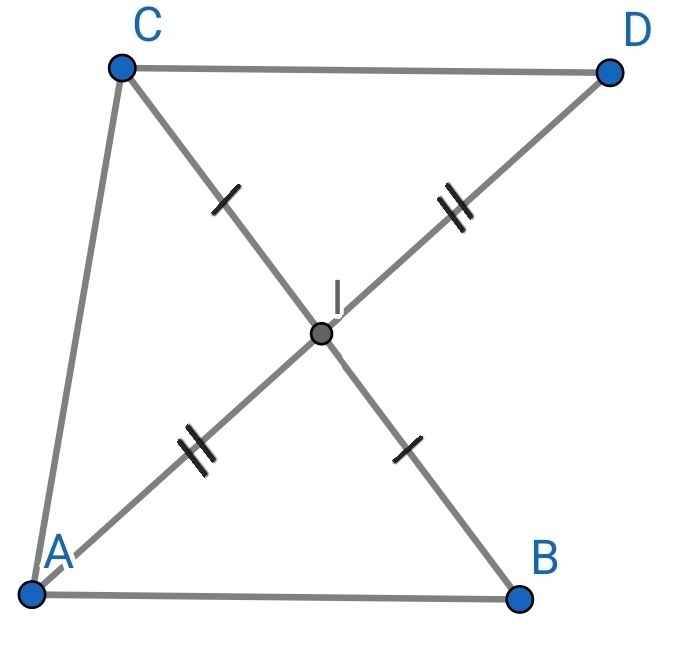 a) Xét ∆CDI và ∆BAI có:

CI = BI (do I là trung điểm của BC)

∠CID = ∠BIA (đối đỉnh)

ID = IA (gt)

⇒ ∆CDI = ∆BAI (c-g-c)

⇒ CD = AB (hai cạnh tương ứng)

b) Do CD = AB (cmt)

Mà AB < AC (gt)

⇒ AC > CD

∆ACD có:

AC > CD (cmt)

⇒ ∠ADC > ∠CAD (quan hệ giữa góc và cạnh đối diện trong tam giác)

⇒ ∠IDC > ∠CAI

Do ∆CDI = ∆BAI (cmt)

⇒ ∠IDC = ∠BAI (hai góc tương ứng)

Mà ∠IDC > ∠CAI

⇒ ∠BAI > ∠CAI

đúng

tui đang trên mạng olm đó

nhanh giúp mình mình hứa sẽ vốt đủ

vote j ạ? ở đây thì bấm đúng bn ạ!