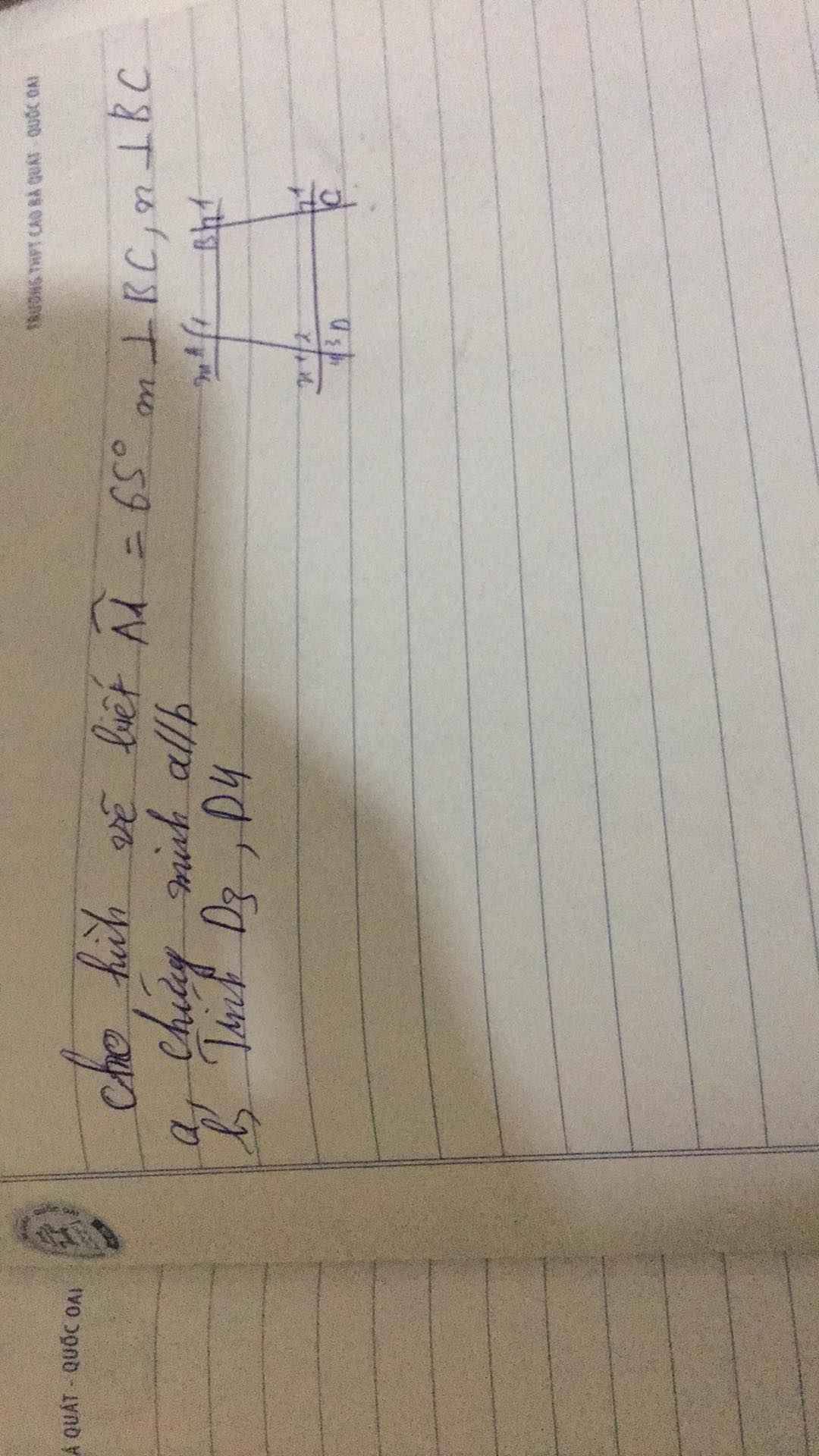a) Sửa đề: Chứng minh m // n

Do m ⊥ BC (gt)

n ⊥ BC (gt)

⇒ m // n

b) Do m // n (cmt)

⇒ ∠D₂ = ∠A₁ = 65⁰

⇒ ∠D₄ = ∠D₂ = 65⁰ (đối đỉnh)

Ta có:

∠D₃ + ∠D₂ = 180⁰ (kề bù)

⇒ ∠D₃ = 180⁰ - ∠D₂

= 180⁰ - 65⁰

= 115⁰

     Thời gian 1 người làm 1 đơn hàng là: 

               28 x 15 : 3 = 140 (ngày)

      20 người làm 1 đơn hàng cần thời gian là:

              140 : 20 = 7 (ngày)

      20 người làm 10 đơn hàng cần thời gian là:

                7 x 10 = 70 (ngày)

                  Đáp số: 70 ngày

\(125\times x-x\times47=25350\\x\times(125-47)=25350\\x\times78=25350\\x=25350:78\\x=325\)

Số tuổi của Quang 5 năm trước là:

$(61-51):2=5$ (tuổi)

Số tuổi của Quang hiện này là:

$5+5=10$ (tuổi)

Số tuổi của ông hiện nay là:

$10+51=61$ (tuổi)

Đáp số: ...

123

😎😎🥺🥺😩😩😫😫🤭🤭

Lời giải:

Theo bài ra ta có:

$a+b=120$

$a\times 0,5+b\times 3=180(1)$

Từ $a+b=120$ nhân 0,5 vào 2 vế ta có:

$a\times 0,5+b\times 0,5=120\times 0,5=60(2)$

Lấy phép tính (1) trừ phép tính (2) thì:

$b\times 3- b\times 0,5=180-60$

$b\times 2,5=120$

$b=120:2,5=48$

$a=120-b=120-48=72$

Cách viết \(x\cdot\left(3,2-1,2\right)\) hay \(x\cdot\left[3.2+\left(-1,2\right)\right]\) đều đúng nhé bạn. Vì có dấu + trước ngoặc nên ta giữ nguyên dấu bên trong và được \(3,2-1,2\).

Cách viết $x\cdot \left(3,2-1,2\right)$ hay $x\cdot \left[3.2+\left(-1,2\right)\right]$ đều đúng nhé bạn. Vì có dấu + trước ngoặc nên ta giữ nguyên dấu bên trong và được $3,2-1,2$.

Ông với Quang nghe như vài thế hệ mà chỉ cách nhau 5 tuổi, em xem lại đề hí

Số tuổi của Quang 5 năm trước là:

$(61-51):2=5$ (tuổi)

Số tuổi của Quang hiện này là:

$5+5=10$ (tuổi)

Số tuổi của ông hiện nay là:

$10+51=61$ (tuổi)

Đáp số: ...

Bài này áp dụng BĐT B.C.S là ra nhé

Ta có \(VT=\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\ge\dfrac{\left(a+b+c\right)^2}{b+c+a}=a+b+c=VP\) 

Dấu "=" xảy ra \(\Leftrightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\Leftrightarrow a=b=c\)

(*) BĐT B.C.S phát biểu như sau:

 Cho \(2n\) số thực \(a_1,a_2,...,a_n,x_1,x_2,...,x_n\), trong đó \(a_i>0,\forall i\in\left\{1,2,...,n\right\}\). Khi đó ta có:

 \(\dfrac{x_1^2}{a_1}+\dfrac{x_2^2}{a_2}+...+\dfrac{x_n^2}{a_n}\ge\dfrac{\left(x_1+x_2+...+x_n\right)^2}{a_1+a_2+...+a_n}\) (*)

Dấu "=" xảy ra \(\Leftrightarrow\dfrac{x_1}{a_1}=\dfrac{x_2}{a_2}=...=\dfrac{x_n}{a_n}\)

Trước tiên, ta chứng minh (*) đúng với \(n=2\). Thật vậy:

Với \(x,y\inℝ;a,b>0\), thì ta cần chứng minh 

\(\dfrac{x^2}{a}+\dfrac{y^2}{b}\ge\dfrac{\left(x+y\right)^2}{a+b}\)

 \(\Leftrightarrow\dfrac{bx^2+ay^2}{ab}\ge\dfrac{\left(x+y\right)^2}{a+b}\)

\(\Leftrightarrow\left(a+b\right)\left(bx^2+ay^2\right)\ge ab\left(x+y\right)^2\)

\(\Leftrightarrow abx^2+a^2y^2+b^2x^2+aby^2\ge abx^2+aby^2+2abxy\)

\(\Leftrightarrow a^2y^2-2abxy+b^2x^2\ge0\)

\(\Leftrightarrow\left(ay-bx\right)^2\ge0\) (luôn đúng)

 Vậy ta có đpcm. Dấu "=" xảy ra \(\Leftrightarrow ay=bx\Leftrightarrow\dfrac{x}{a}=\dfrac{y}{b}\)

 Để chứng minh với \(n\ge3\) thì bạn chỉ cần dùng nhiều lần BĐT cho 2 phân thức là được.

 VD: \(\dfrac{x^2}{a}+\dfrac{y^2}{b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y\right)^2}{a+b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y+z\right)^2}{a+b+c}\)

Vậy BĐT được chứng minh.

Gọi hai số cần tìm là a và b. Theo đề bài, ta có các điều kiện sau: 1. Hiệu của hai số là 0,6: a - b = 0,6 2. Thương của hai số là 0,6: a / b = 0,6 Để giải hệ phương trình này, ta có thể sử dụng phương pháp thế hoặc phương pháp đại số. Sử dụng phương pháp thế, ta có: a = 0,6 + b Thay vào phương trình thứ hai: (0,6 + b) / b = 0,6 0,6 + b = 0,6b 0,6b - b = 0,6 0,6b = 0,6 b = 1 Thay b = 1 vào phương trình a = 0,6 + b: a = 0,6 + 1 a = 1,6 Vậy hai số cần tìm là a = 1,6 và b = 1.

mình sẽ tích cho ai nhanh nhất