B1.Cho hình thang abcd vuông tại a và d cho biết ab=12cm cd=18cm,ad=8cm.Tính diện tích hình thang abcd, tỉ số phần trăm diện tích tam giác bcd và diện tích hình thang abcd
B2.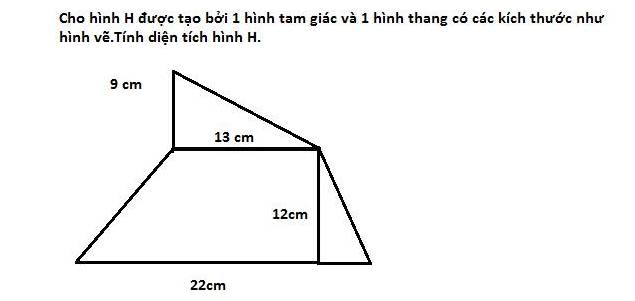
Làm đc tớ xin tặng coin ạ(GẤP);vvv
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) 5 + (-4) = 1
2) (-8) + 2 = -6
3) 8 + (-2) = 6
4) 11 + (-3) = 8
5) (-11) + 2 = -9
6) (-7) + 3 = -4
7) (-5) + 5 = 0
8) 11 + (-12) = -1
9) (-18) + 20 = 2
10) (15) + (-12) = 3
11) (-17) + 17 = 0
12) 16 + (-2) = 14
13) (30) + (-14) = 16
14) (-19) + 20 = 1
15) (-18) + 15 = -3
16) (10) + (-6) = 4
17) (-28) + 14 = -14
18) 15 + (-30) = -15
19) (15) + (-4) = 11
20) (-21) + 11 = -10
21) 8 + (-22) = -14
22) (-15) + 4 = -11
23) (-3) + 2 = -1
24) 17 + (-14) = 3
25) 17 + (-14) = 3

gọi cr lúc sau là a
cd lúc sau là b
chu vi lúc sau là c
(a+b)*2=

Câu 1:
$A=(1+5+5^2)+(5^3+5^4+5^5)+...+(5^{2016}+5^{2017}+5^{2018})$
$=(1+5+5^2)+5^3(1+5+5^2)+....+5^{2016}(1+5+5^2)$
$=(1+5+5^2)(1+5^3+...+5^{2016})$
$=31(1+5^3+...+5^{2016})\vdots 31$ (đpcm)
Câu 2:
$2x+7\vdots 2x-2$
$\Rightarrow (2x-2)+9\vdots 2x-2$
$\Rightarrow 9\vdots 2x-2$
$\Rightarrow 2x-2$ là ước của $9$
Mà $2x-2$ là số chẵn với mọi $x$ nguyên, còn $Ư(9)\in \left\{\pm 1; \pm 3; \pm 9\right\}$ (không có ước nào chẵn)
$\Rightarrow$ không tồn tại $x$ nguyên thỏa mãn yêu cầu đề bài.

Trong thùng còn lại số ki-lô-gam đường là:
72:6=12(kg)

Lời giải:
a. Vì $A,D$ đối xứng nhau qua $M$ nên $M$ là trung điểm $AD$
Tứ giác $ABDC$ có 2 đường chéo $AD, BC$ cắt nhau tại trung điểm $M$ của mỗi đường nên là hình bình hành.
Mà $\widehat{BAC}=90^0$ nên $ABDC$ là hình chữ nhật.
b.
Vì $ABDC$ là hcn nên:
$AB\parallel DC, AB=DC$ (1)
Vì $E$ đối xứng với $A$ qua $B$ nên $A,B,E$ thẳng hàng và $AB=BE$(2)
Từ $(1); (2)\Rightarrow BE\parallel DC, BE=DC$
Tứ giác $BEDC$ có 2 cạnh đối nhau $BE, DC$ song song và bằng nhau nên $BEDC$ là hình bình hành.
c.
$BEDC$ là hbh nên $BC\parallel ED$ và $BC=ED$
Ta có:
$BC=ED$, mà $BC=2BM$ nên $ED=2BM$
$BC\parallel ED\Rightarrow BM\parallel ED$. Áp dụng định lý Talet:
$\frac{EK}{KM}=\frac{ED}{BM}=\frac{2BM}{BM}=2$
$\Rightarrow EK=2KM$ (đpcm)
Bài 1:
Diện tích ABCD: $\frac{(AB+CD)\times AD}{2}=\frac{(12+18)\times 8}{2}=120$ (cm2)
Diện tích $BCD$ là: $CD\times AD:2=8\times 18:2=72$ (cm2)
Tỉ số phần trăm diện tích tam giác BCD và hình thang ABCD là:
$72:120\times 100=60$ (%)
Bài 2:
Diện tích hình tam giác: $9\times 12:2=58,5$ (cm2)
Diện tích hình thang: $(13+22)\times 12:2=210$ (cm2)
Diện tích hình H là: $58,5+210=268,5$ (cm2)