Hai lớp 7A và 7B đi lao động trồng cây. Biết rằng tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 và lớp 7B trồng nhiều hơn lớp 7A là 20 cây. Tính số cây mỗi lớp đã trồng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi số đó là abcd
Theo bài cho : abcd x 4 = dcba
=> abcd = dcba : 4
Vì dcba là số có 4 chữ số nên dcba < 10> abcd = dcba : 4 < 10> a ≤≤ 2
Hơn nữa , a phải là chữ số chẵn khác 0 nên a = 2
=> 2bcd x 4 = dcba => d > 2 và kết quả d x 4 có chữ số tận cùng bằng 2
=> d = 8
Vậy ta có: 2bc8 x 4 = 8cb2 => phép nhân 4 x b không có nhớ
Mà theo dấu hiệu chia hết cho 4 => b2 chia hết cho 4 => b có thể bằng 1;3;52;72; 92
=> b chỉ có thể bằng 1
=> 21c8 x 4 = 8c12 => 8000 + 400 + 40c + 32 = 8000 + 100c + 12
=> 420 = 60c => c = 420 : 60 = 7
Vậy số cần tìm là: 2178
a) Gọi số cần tìm là abcd
Nếu nhân số đó vs 4 thì ta dc số ấy viết theo thứ tự ngược lại là:
abcd.4=dcba
=>dcba chia hết cho 4
Vậy a thuộc 0;2;4;6;8} và a<3
=>a=2
dcba=2bcd.4>2000.4=8000
=> d thuộc {8;9}
Mà 4d<10
->d=8
8cd2=2bc8.4
=>8cb2 chia hết cho 4=>b2 chia hết cho 4
=>b thuộc {1;3;5;7;9}
Mà 4b<10
=>b=1
8c12=21c8.4
4c+3 có tận cùng là 1
=> 4c là số chẵn và=8
=>c thuộc {2;7}
Vs c=2: 0 thỏa mãn vì 2128.4e8212
Vs c=7 thỏa mãn vì 2178.4=8712
Vậy abcd=2178

\(\text{A = }\frac{\text{-1}}{\text{2011}}-\frac{\text{3}}{\text{11}^2}-\frac{\text{5}}{\text{11}^2.\text{11}}-\frac{\text{7}}{\text{11}^2.\text{11}^2}=\text{ }\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(3-\frac{\text{5}}{\text{11}}-\frac{\text{7}}{\text{11}^2}\right)\)
\(\text{B = }\text{ }\frac{\text{-1}}{\text{2011}}-\frac{7}{\text{11}^2}-\frac{5}{\text{11}^2.\text{11}}-\frac{3}{\text{11}^2.\text{11}^2}=\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(7-\frac{5}{\text{11}}-\frac{3}{\text{11}^2}\right)\)
\(\text{Vì }3-\frac{\text{5}}{\text{11}}-\frac{\text{7}}{\text{11}^2}< 7-\frac{5}{\text{11}}-\frac{3}{\text{11}^2}\)
\(\Rightarrow\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(3-\frac{\text{5}}{\text{11}}-\frac{\text{7}}{\text{11}^2}\right)>\frac{\text{-1}}{\text{2011}}-\frac{\text{1}}{\text{11}^2}.\left(7-\frac{5}{\text{11}}-\frac{3}{\text{11}^2}\right)\)
=> A > B
Vậy A > B

a có: xOy=120 (đề cho) và oAt= 60 (đề cho) ta lại có xOy+tAo=120 + 60 =180 (kề bù) mà 2 góc xOy và tAo ở vị trí trong cùng phía suy ra : oy // At mà AT' là tia đối của tia AT suy ra : tt' // oy
b) ta có xOy = xAt ( 2 góc đồng vị , oy // at ) mà xoy= 120 suy ra xAt=120 vì om là tia phân gica của xOy nên xom = moy = xoy/2 = 60 và on là tia phân giác của xAt xAn=nAt = xAt/2 = 60 mà xOy = xAt ( = 120 ) ta có xAn = xOm (= 60 ) mà 2 góc xAn và xOm ở vị tí đồng vị suy ra : An // Om
các số nhớ thêm độ đấy nhé
k đi
O y x A t m m n K L z
a) góc AOy = 120 0 => góc AOm = 600
Ta lại có góc AOt = 600 => At // Oy ( Cặp góc so le trong )
b) Om ko thể // An

Đánh số các người tham gia từ \(A_1\)đến \(A_{16}\).
Giả sử \(A_1\)thắng nhiều nhất.
Có: \(\frac{16\times15}{2}=120\)(ván đấu) suy ra \(A_1\)thắng \(\ge\frac{120}{16}=7,5\)
suy ra \(A_1\)thắng ít nhất \(8\)ván.
Không mất tính tổng quát, giả sử \(A_1\)thắng \(A_2,A_3,...,A_9\).
Giả sử trong những người này \(A_2\)thắng nhiều nhất.
\(A_2,...,A_9\)đánh \(\frac{8\times7}{2}=28\)(ván) suy ra \(A_2\)thắng \(\ge\frac{28}{8}=3,5\)
suy ra \(A_2\)thắng ít nhất \(4\)ván (khi đấu với \(A_3,...,A_9\))
Giả sử \(A_2\)thắng \(A_3,...,A_6\).
Giả sử \(A_3\)thắng nhiều nhất trong những người này.
\(A_3,...,A_6\)đánh \(\frac{4\times3}{2}=6\)(ván) suy ra \(A_3\)thắng \(\ge\frac{6}{4}=1,5\)
suy ra \(A_3\)thắng ít nhất \(2\)ván.
Giả sử \(A_3\)thắng \(A_4,A_5\).
Khi đó giả sử \(A_4\)thắng \(A_5\)thì ta có dãy thỏa mãn là: \(A_1,A_2,A_3,A_4,A_5\).
Ta có đpcm.


Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?
A. 10 cm, 22 cm
B. 10 cm, 24 cm
C. 12 cm, 24 cm
D. 15 cm, 24 cm
Gọi độ dài 2 cạnh là \(x\), \(y\)( \(x\), \(y\)> 0 )
Theo định lý Pitago ta có : \(\frac{x}{5}=\frac{y}{12}\)\(\Rightarrow\)\(\frac{x^2}{25}=\frac{y^2}{144}=\frac{x^2+y^2}{25+144}\)
= \(\frac{676}{169}=4\)
\(\Leftrightarrow\)\(x^2=25.4\)
\(\Leftrightarrow\)\(x^2=100\)
\(\Leftrightarrow\)\(x=10\)cm
Ta lại có :
\(\Leftrightarrow\)\(y^2=144.4\)
\(\Leftrightarrow\)\(y^2=576\)
\(\Leftrightarrow\)\(y=24\)
Vậy ...................
=> Chọn B
Hok tốt

a, Xét ΔAIC vuông tại I và ΔBIC vuông tại I có:
CA=CB (=10 cm)
CI là cạnh chung
⇒ΔAIC=ΔBIC (trường hợp đặc biệt ,cạnh huyền, cạnh góc vuông)
⇒IA=IB (2 cạnh tương ứng)
b, Ta có: IA+IB=AB
mà AB=12 cm
IA=IB (cmt)
⇒2IA=12
⇒IA=12÷2=6 cm
Ta có: ΔAIC vuông tại I có:
IC²+IA²=CA² (định lí Py-ta-go)
mà IA=6 cm(gt)
CA=10 cm (gt)
⇒IC²+6²=10²
⇒IC²+36=100
⇒IC²=100-36=64
⇒IC=8 cm
c, Ta có:CA=CB (10 cm)
⇒ΔABC cân tại C
⇒∠CAB=∠CBA (2 cạnh ở đáy củaΔ cân )
Ta có: IH⊥AC tại H (gt)⇒ΔAIH vuông tại H
IK⊥BC tại K (gt)⇒ΔBIK vuông tại K
Xét ΔAIH vuông tại H và ΔBIK vuông tại K có:
AI=IB (cmt)
∠CAB=∠CBA (cmt)
⇒ΔAIH=ΔBIK (trường hợp đặc biệt,canh huyền,góc nhọn)
⇒IH=IK (2 cạnh tương ứng)

Số 1 vừa là số tự nhiên, vừa là số nguyên, vừa là số hữu tỉ
Bài làm:
Gọi số cây trồng được của lớp 7A, 7B lần lượt là x (cây); y (cây).
Tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 nghĩa là x : y =0,8 hay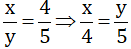 .
.
Lớp 7B trồng nhiều hơn lớp 7A là 20 cây nghĩa là y – x = 20.
Theo tính chất dãy tỉ số bằng nhau
Vậy Lớp 7A trồng được 80 cây
Lớp 7B trồng được 100 cây
chúc bn hok tốt