cho tam giác ABC, CN, BM là trung tuyến. BM<CN, chứng minh AB<AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do \(x,y,z\) là số chính phương nên chỉ có thể chia 3 và 4 dư 0 hoặc dư 1.
Theo nguyên lí Dirichlet, tồn tại 2 số có cùng số dư khi chia cho 3 và 4. Không mất tính tổng quát, giả sử là \(x,y\)
\(\Rightarrow\left\{{}\begin{matrix}x-y⋮3\\x-y⋮4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}B⋮3\\B⋮4\end{matrix}\right.\) \(\Rightarrow B⋮12\), đpcm

Lời giải:
a.
$Q(x)=(3x^4+x^3+2x^2+x+1)-P(x)=(3x^4+x^3+2x^2+x+1)-(2x^4-x^2+x-2)$
$=3x^4+x^3+2x^2+x+1-2x^4+x^2-x+2$
$=x^4+x^3+3x^2+3$
b.
$H(x)=P(x)-(x^4-x^3+x^2-2)=(2x^4-x^2+x-2)-(x^4-x^3+x^2-2)$
$=2x^4-x^2+x-2-x^4+x^3-x^2+2$
$=x^4+x^3-2x^2+x$

\(\dfrac{x}{y}=\dfrac{6}{5}\Leftrightarrow\dfrac{x}{6}=\dfrac{y}{5}\)
\(\dfrac{x+y}{6+5}=\dfrac{22}{11}=2\)
\(\dfrac{x}{6}=2\Rightarrow x=12\\ \dfrac{y}{5}=2\Rightarrow y=10\)
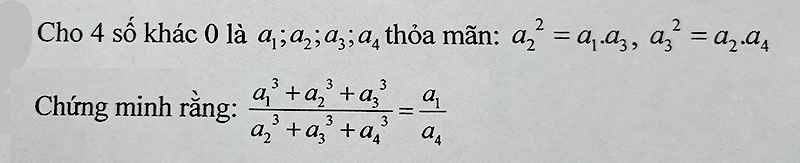


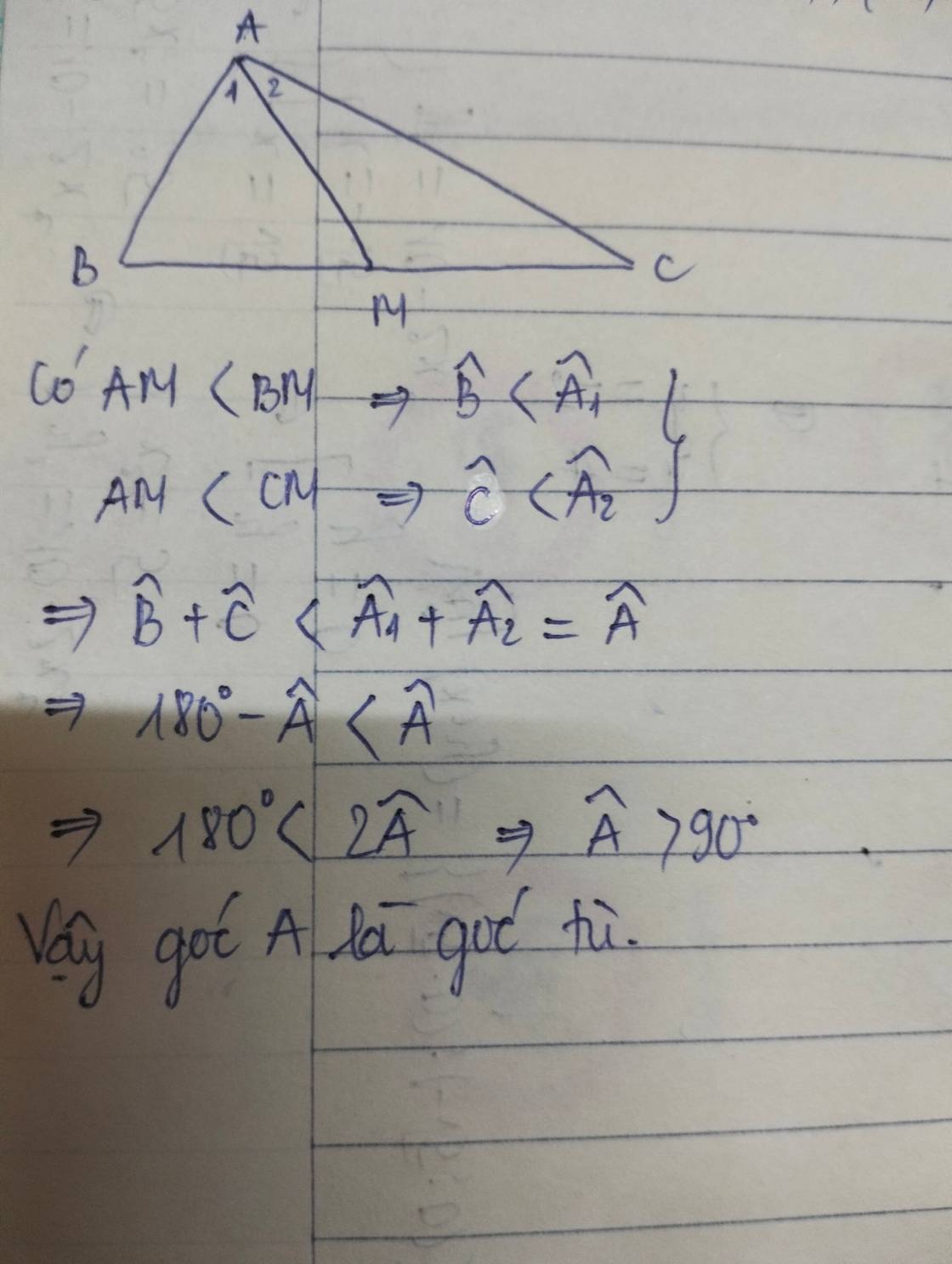

mn ơi