cho tam giác ABC cân tại A, điểm D nằm giữa 2 điểm B và C
a, Khi D di động trên đoạn thẳng BC thì độ dài đoạn thẳng AD thay đổi xác định vị trí của điểm D để độ dài đoạn thẳng AD nhỏ nhất
b, Giải thích vì sao độ dài đoạn AD nhỏ hơn cạnh bên của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho S= \(1\times2^0+2\times2^1+3\times3^2+...+2019\times2^{2018}\)
so sánh S với 22018 x 2019 + 2019

Lời giải:
** Sửa lại đề:
$S=1.2^0+2.2^1+3.2^2+...+2019.2^{2018}$
$2S=1.2^1+2.2^2+3.2^3+...+2018.2^{2018}+2019.2^{2019}$
$\Rightarrow 2S-S=2019.2^{2019}-(2^0+2^1+2^2+2^3+...+2^{2018})$
$\Rightarrow S=2019.2^{2019}-(2^0+2^1+2^2+2^3+...+2^{2018})$
Xét:
$M=2^0+2^1+2^2+..+2^{2018}$
$2M=2^1+2^2+2^3+...+2^{2019}$
$\Rightarrow 2M-M=2^{2019}-2^0$
$\Rightarrow M=2^{2019}-1$
$S=2019.2^{2019}-M = 2019.2^{2019}-(2^{2019}-1)=2018.2^{2019}+1$
Xét hiệu:
$S-(2019.2^{2018}+2019)=2018.2^{2019}+1-2019.2^{2018}-2019$
$=2^{2018}(2018.2-2019)+1-2019$
$=2^{2018}.2017-2018>0$
$\Rightarrow S> 2019.2^{2018}+2019$

Lời giải:
a.
Đặt $\frac{a}{5}=\frac{b}{4}=k\Rightarrow a=5k, b=4k$
Khi đó:
$a^2-b^2=1$
$\Rightarrow (5k)^2-(4k)^2=1$
$\Rightarrow 9k^2=1\Rightarrow k^2=\frac{1}{9}\Rightarrow k=\frac{1}{3}$ hoặc $k=\frac{-1}{3}$
Nếu $k=\frac{1}{3}$ thì:
$a=5k=\frac{5}{3}; b=4k=\frac{4}{3}$
Nếu $k=\frac{-1}{3}$ thì:
$a=5k=\frac{-5}{3}; b=4k=\frac{-4}{3}$
b.
Đặt $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k$
$\Rightarrow a=2k; b=3k; c=4k$
Khi đó:
$a^2-b^2+2c^2=108$
$\Rightarrow (2k)^2-(3k)^2+2(4k)^2=108$
$\Rightarrow 27k^2=108$
$\Rightarrow k^2=4\Rightarrow k=\pm 2$
Nếu $k=2$ thì:
$a=2k=4; b=3k=6; c=4k=8$
Nếu $k=-2$ thì:
$a=2k=-4; b=3k=-6; c=4k=-8$

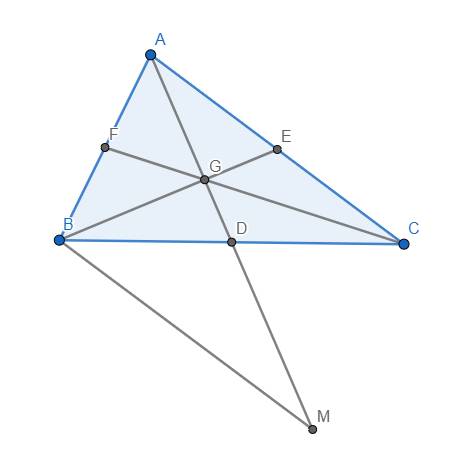
Gọi G là trọng tâm của tam giác ABC. Qua B kẻ đường thẳng song song với AC cắt AD tại M.
Khi đó \(\widehat{DCA}=\widehat{DBM}\) (2 góc so le trong)
Xét 2 tam giác DAC và DMB, ta có:
\(\widehat{DCA}=\widehat{DBM}\left(cmt\right);\) \(DC=DB\) (do AD là trung tuyến của tam giác ABC) và \(\widehat{ADC}=\widehat{BDM}\) (2 góc đối đỉnh)
Do đó \(\Delta DAC=\Delta DMB\left(g.c.g\right)\)
\(\Rightarrow MB=AC\) và \(DA=DM\Rightarrow\) D là trung điểm AM \(\Rightarrow DM=2DA\)
Trong tam giác ABM, ta có \(AM< AB+BM\)
Lại có \(DM=2DA;MB=AC\left(cmt\right)\) \(\Rightarrow2AD< AB+AC\)
\(\Rightarrow AD< \dfrac{AB+AC}{2}\)
\(\Rightarrow AD< \dfrac{AB}{2}+\dfrac{AC}{2}\)
\(\Rightarrow AD< BF+CE\) (1)
Trong tam giác GBF, có \(BF< GB+GF\), trong tam giác GCE có \(CE< GC+GE\)
Cộng theo vế 2 bất đẳng thức trên, thu được \(BF+CE< GF+GB+GE+GC\)
hay \(BF+CE< \left(GB+GE\right)+\left(GC+GF\right)\)
hay \(BF+CE< BE+CF\) (2)
Từ (1) và (2) \(\Rightarrow AD< BE+CF\)
Hoàn toàn tương tự, ta chứng minh được \(BE< AD+CF\) và \(CF< AD+BE\). Do đó AD, BE, CF là độ dài 3 cạnh của 1 tam giác (đpcm)

Gọi số sách sau khi chuyển của 3 tủ lần lượt là \(x,y,z\) \(\left(x,y,z\inℕ^∗\right)\) \(\left(x,y,z< 2250\right)\)
Ta có: \(\dfrac{x}{16}=\dfrac{y}{15}=\dfrac{z}{14}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{16}=\dfrac{y}{15}=\dfrac{z}{14}=\dfrac{x+y+z}{16+15+14}=\dfrac{2250}{45}=50\)
=> \(\left\{{}\begin{matrix}\dfrac{x}{16}=50\\\dfrac{y}{15}=50\\\dfrac{z}{14}=50\\\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=16.50=800\\y=15.50=750\\z=14.50=700\\\end{matrix}\right.\left(tmdk\right)\)
Do đó số sách sau khi chuyển của tủ 1 là 800, tủ 2 là 750 và tủ 3 là 700 cuốn
Vậy trước khi chuyển 100 cuốn từ tủ 1 sang tủ 3 thì
+) Tủ 1 có: 800 + 100 = 900 cuốn
+) Tủ 2 có: 750 cuốn
+) Tủ 3 có: 700 – 100 = 600 cuốn

\(a\)) Xét tứ giác \(ABPC\) có
\(AK=KP\left(gt\right)\)
\(BK=KC\left(gt\right)\)
\(\Rightarrow\) Tứ giác \(ABPC\) là hình bình hành
\(\Rightarrow AC=BP\) và \(AC//BP\).

\(\dfrac{x+1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\)
\(=\dfrac{3x+3}{6}=\dfrac{4y+12}{16}+\dfrac{5z-25}{30}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x+1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{3x+3}{6}=\dfrac{4y+12}{16}+\dfrac{5z-25}{30}=\dfrac{5x-25-3x-3-4y-12}{30-16-6}=\dfrac{50-40}{8}=\dfrac{10}{8}=\dfrac{5}{4}\)
\(\Rightarrow\dfrac{x+1}{2}=\dfrac{5}{4}\Rightarrow x+1=2,5\)
\(\Rightarrow x=1,5.\)
\(\Rightarrow\dfrac{y+3}{4}=\dfrac{5}{4}\Rightarrow y+3=5\)
\(\Rightarrow y=2\)
\(\Rightarrow\dfrac{z-5}{6}=\dfrac{5}{4}\Rightarrow z-5=7,5\)
\(\Rightarrow z=12,5.\)
Vậy các số \(\left(x;y;z\right)\) cần tìm lần lượt là \(\left(1,5;2;12,5\right)\)

Ta có: \(MN=MP\)
\(\Rightarrow\Delta MNP\) cân tại M
\(\Rightarrow\widehat{N}=\widehat{P}\) (hai góc ở đáy)
Mà: \(\widehat{M}+\widehat{N}+\widehat{P}=180^o\)
\(\Rightarrow2\widehat{P}+\widehat{P}+\widehat{P}=180^o\)
\(\Rightarrow4\widehat{P}=180^o\Rightarrow\widehat{P}=\widehat{N}=45^o\)
\(\Rightarrow\widehat{M}=2\widehat{P}=2\cdot45=90^o\)
tui moi hoc lop 2 ma tui qua lop 7 de xem co coTu Anh khong va phan boi co Tu Anh

Nối B với D.
Ta có SABM=SAMC mà SABM = SDMC
Suy ra SDMC = SAMC = SABM = SBMD.
(Vì sau khi nối thì hình thành hình thoi)

Lời giải:
a. Gọi hệ số tỉ lệ của số thóc so với số gạo là $k$
Ta có: $100=60k\Rightarrow k=\frac{100}{60}=\frac{5}{3}$
b.
Nếu muốn có 150kg gạo thì cần mang xay số thóc là:
$150.\frac{5}{3}=250$ (kg)