A, $25\times78-146\times38+25\times22+146\times28$

$=25\times(78+22)-146\times(38-28)$

$=25\times100-146\times10$

$=2500-1460=1040$

B, $34\times17+34\times71+34\times12-34\times10$

$=34\times(17+71+12-10)$

$=34\times(88+2)$

$=34\times90=3060$

Ta có: 

\(S=\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\\ \Rightarrow\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}+\dfrac{3}{14}< S< \dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}+\dfrac{3}{10}\\ \Rightarrow\dfrac{3+3+3+3+3}{14}< S< \dfrac{3+3+3+3+3}{10}\\ \Rightarrow\dfrac{15}{14}< S< \dfrac{3}{2}\\ \Rightarrow\dfrac{14}{14}< S< \dfrac{3}{2}\\ \Rightarrow1< S< \dfrac{3}{2}\)

=> S không phải số tự nhiên vì giữa 1 và `3/2` không có số tự nhiên 

7 hoặc -7

\(x^2\) = 49

\(x^2\) = 7²

|\(x\)| = 7

\(\left[{}\begin{matrix}x=-7\\x=7\end{matrix}\right.\)

Vậy \(x\) \(\in\) {- 7; 7}

Bài 5:

a: Số góc tạo thành là \(15\left(15-1\right)=15\cdot14=210\left(góc\right)\)

Bởi vì với n đường thẳng cắt nhau sẽ tạo ra n(n-1) góc

b: Số góc tạo thành là 435 góc nên \(\dfrac{n\left(n-1\right)}{2}=435\)

=>n(n-1)=870

=>\(n^2-n-870=0\)

=>(n-30)(n+29)=0

=>\(\left[{}\begin{matrix}n=30\left(nhận\right)\\n=-29\left(loại\right)\end{matrix}\right.\)

Vậy: n=30

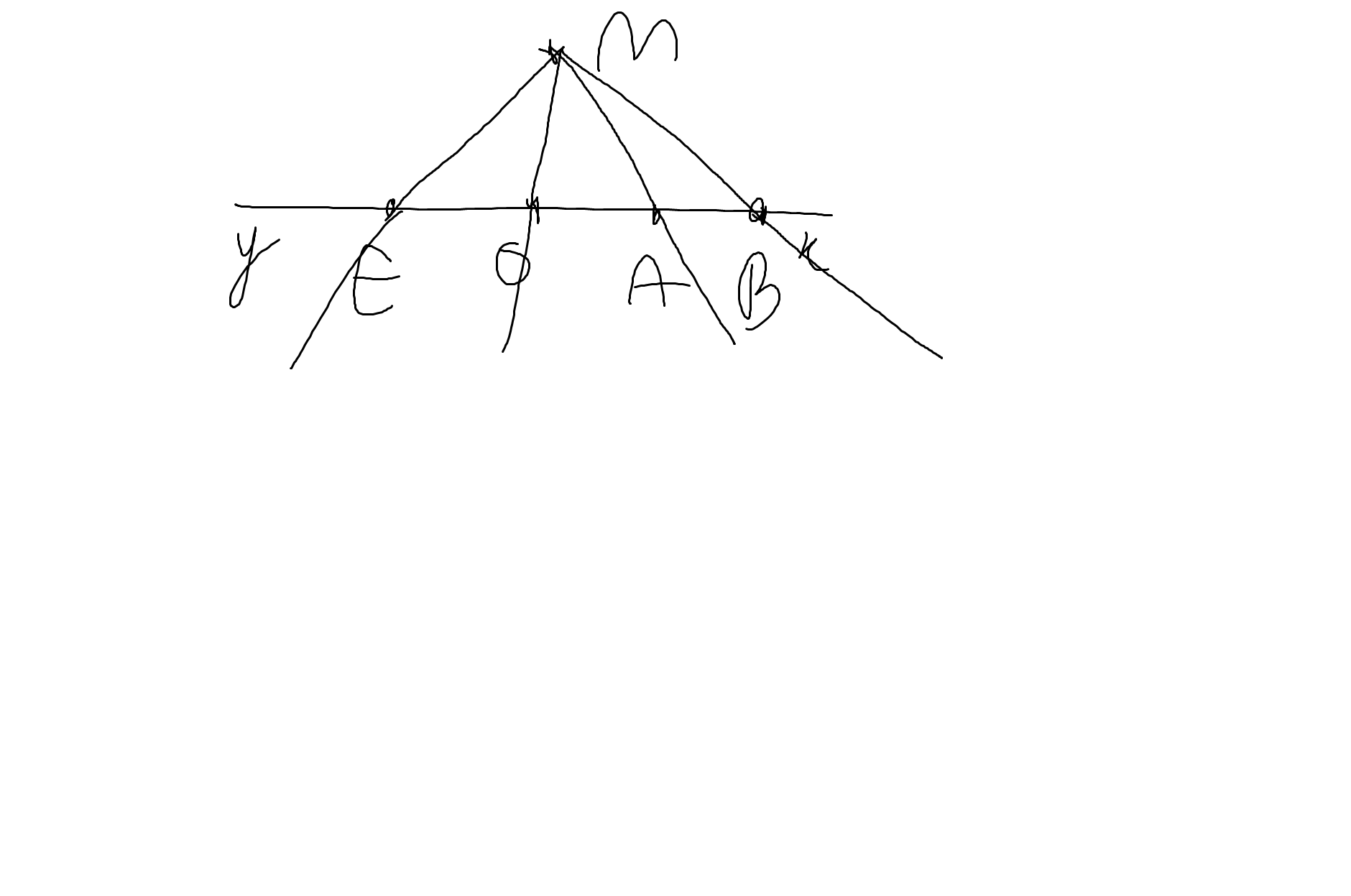
Bài 4:

a: Trên tia Ox, ta có: OA<OB

nên điểm A nằm giữa hai điểm O và B

=>Điểm A có nằm trong góc OMB

b: Vì OE và OB là hai tia đối nhau

nên O nằm giữa E và B

=>O nằm trong góc EMB

Vì A nằm giữa O và B

và O nằm giữa E và B

nên A nằm giữa E và B

=>A nằm trong góc EMB

c: Các cặp tia đối nhau là:
OE,OB

AE,Ax

BE,Bx

Ex,Ey

d: Các góc bẹt trong hình vẽ là: \(\widehat{xEy};\widehat{xOy};\widehat{xBy};\widehat{xAy}\)

Giúp mik bài 1,2,3 với

a: A={1;2;3;4;5;6}; B={1;3;5;7;9}

=>C={2;4;6}

b: D={7;9}

c: E={1;3;5}

Ư(54)={1;-1;2;-2;3;-3;6;-6;9;-9;18;-18;27;-27;54;-54}

=>Các số vừa là bội của 3 vừa là ước của 54 là 3;-3;6;-6;9;-9;18;-18;27;-27;54;-54

Giải: 54 = 2.3³

Ư(54) = {-54; -27; - 18; - 9; - 6; -3; - 2; -1; 1; 2; 3; 6; 9; 18; 27; 54}

Những số vừa là ước của 54 vừa là bội của 3 là các số thuộc tập B trong đó:

B = {- 54; - 27; - 18; - 9; - 6; - 3; 3; 6; 9; 18; 27; 54} 

Liệt kê theo cặp các ước của 180.

Ư(180) = {1; 180; 2; 90; 3; 60; 4; 45; 5; 36; 6; 30; 9; 20; 10; 18; 15; 12}

P là tập hợp các ước không nguyên tố của 180. 

suy ra, P = {1; 180; 90; 60; 4; 45; 36; 6; 30; 9; 20; 10; 18; 15; 12}.

Vậy tập hợp P có 15 phần tử.

Vậy số phần tử của tập hợp P là: 15 phần tử

180 = 2².3².5

Số ước số của 180 là: (2 + 1).(2 + 1).(1 + 1) = 18 (ước)

Số ước số là số nguyên tố của 180 là 3 ước đó là các ước 2; 3; 5

Số ước số không phải là số nguyên tố của 180 là: 18 - 3 = 15 (ước)

Kết  luận P có 15 phần tử

Đề sai, em xem lại đề nhé

x+(x+1)+(x+2)+...+(x+10)=88

=>11x+(1+2+...+10)=88

=>11x+55=88

=>x+5=8

=>x=3

Bài 1:

\(\dfrac{x-2}{5}=\dfrac{-2}{2y+1}\)

=>\(\left(x-2\right)\left(2y+1\right)=5\cdot\left(-2\right)=-10\)

mà 2y+1 lẻ

nên \(\left(x-2;2y+1\right)\in\left\{\left(2;-5\right);\left(-2;5\right);\left(-10;1\right);\left(10;-1\right)\right\}\)

=>\(\left(x;y\right)\in\left\{\left(4;-3\right);\left(0;2\right);\left(-8;0\right);\left(12;-1\right)\right\}\)

Bài 2:

a: \(\left(2x-1\right)^2+4>=4\forall x\)

=>\(B=\dfrac{20}{\left(2x-1\right)^2+4}< =\dfrac{20}{4}=5\forall x\)

Dấu '=' xảy ra khi 2x-1=0

=>\(x=\dfrac{1}{2}\)

b: \(\left(x^2+1\right)^2>=1\forall x\)

=>\(\left(x^2+1\right)^2+5>=1+5=6\forall x\)

=>\(C=\dfrac{10}{\left(x^2+1\right)^2+5}< =\dfrac{10}{6}=\dfrac{5}{3}\forall x\)

Dấu '=' xảy ra khi x=0

BÀI 4A

\(\dfrac{1}{-2}+\dfrac{1}{-6}+\dfrac{1}{-12}+\dfrac{1}{-20}+\dfrac{1}{-30}+\dfrac{1}{-42}+\dfrac{1}{-56}+\dfrac{1}{-72}+\dfrac{1}{-90}\\ =-1\cdot\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\right)\\ =-1\cdot\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\right)\\ =-1\cdot\left(\dfrac{1}{1}-\dfrac{1}{10}\right)=-1\cdot\dfrac{9}{10}=-\dfrac{9}{10}\)