Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$5x^2+5y^2+8xy-2x+2y+2=0$
$\Leftrightarrow 4(x^2+y^2+2xy)+(x^2-2x+1)+(y^2+2y+1)=0$
$\Leftrightarrow 4(x+y)^2+(x-1)^2+(y+1)^2=0$
Ta thấy: $(x+y)^2\geq 0; (x-1)^2\geq 0; (y+1)^2\geq 0$ với mọi $x,y$
Do đó để tổng của chúng bằng $0$ thì:
$(x+y)^2=(x-1)^2=(y+1)^2=0$
$\Rightarrow x=1; y=-1$
Khi đó:
$M=0^2+(1-2)^{2024}+(-1+1)^{2025}=0+1+0=1$

N = x² - 2xy + 3y² - 4y + 2023
= (x² - 2xy + y²) + (2y² - 4y) + 2023
= (x - y)² + 2(y² - 2y + 1) + 2021
= (x - y)² + 2(y - 1)² + 2021
Do (x - y)² ≥ 0 với mọi x, y ∈ R
⇒ (y - 1)² ≥ 0 với mọi y ∈ R
⇒ (x - y)² + 2(y - 1)² ≥ 0 với mọi x, y ∈ R
⇒ (x - y)² + 2(y - 1)² + 2021 > 0 với mọi x, y ∈ R
Vậy N luôn dương với mọi x, y ∈ R

a, 08/01/2023 là tròn 1 tuần kể từ 01/01/2023 (Chủ nhật) vậy 08/01/2023 cũng là chủ nhật
b, Từ 08/01/2023 đến 08/03/2023 là tròn 2 tháng có: 31 ngày (tháng 1) và 28 ngày (tháng 2 năm không nhuận) vậy tổng thời gian giữa 2 khoảng này là 59 ngày
Ta có: 59:7 = 8 (tuần) (dư 3 ngày)
=> 08/03/2023 rơi vào thứ tư

Lời giải:
$S=1-3+3^2-3^3+...-3^{2021}+3^{2022}$
$3S=3-3^2+3^3-3^4+...-3^{2022}+3^{2023}$
$\Rightarrow S+3S=1+3^{2023}$
$\Rightarrow 4S=1+3^{2023}$
$\Rightarrow 4S-3^{2023}=1$
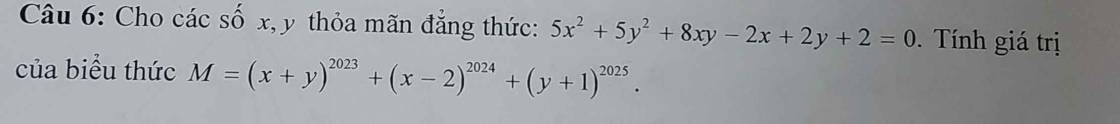
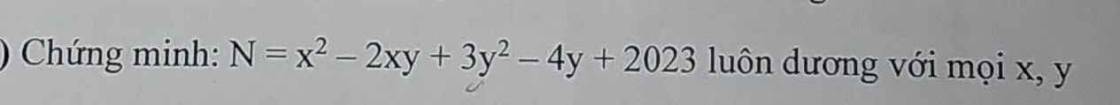
Lời giải:
** Sửa đề: $A=\frac{ab}{(b-c)(c-a)}+\frac{bc}{(c-a)(a-b)}+\frac{ac}{(a-b)(b-c)}$
\(A=\frac{ab(a-b)+bc(b-c)+ac(c-a)}{(a-b)(b-c)(c-a)}=\frac{(a^2b+b^2c+c^2a)-(ab^2+bc^2+ca^2)}{-[(a^2b+b^2c+c^2a)-(ab^2+bc^2+ca^2)]}=-1\)